Динамический хаос и фундаментальные ограничения в области прогноза

 

Авторы: Г.Г.Малинецкого, С.П.Курдюмова Д.С.Чернавский

 

Источник: http://spkurdyumov.narod.ru/OTCHET/OTCHET.htm

 

До 60-ых годов предполагалось, что есть два класса процессов. Первые - процессы, которые описываются динамическими системами, где будущее однозначно определяется прошлым. Для них, как думали раньше, у нас есть полная предсказуемость. Великий Лаплас, имея в виду такие системы, говорил (если перевести на наш язык), что, располагая достаточно мощными компьютерами, мы сможем заглянуть как угодно далеко в будущее и как угодно далеко в прошлое. Второй класс процессов - это процессы, где будущее не зависит от прошлого. Мы бросаем игральную кость, и выпадает случайная величина, никак не связанная с тем, что выпадало раньше.

В 70-е годы было понято, что есть третий, очень важный класс процессов, которые формально описываются динамическими системами, как этот маятник. Но, вместе с тем, поведение которых может быть предсказано только на небольшой промежуток времени. А дальше исследователи будут вынуждены иметь дело со статистикой. Для этой игрушки можно написать простую линейную модель, которая позволит нам предсказать, в каком положении, например, окажутся маленькие шарики через пять колебаний большого шарика внизу (естественный промежуток здесь - период колебаний большого шарика.). Используя современные информационные технологии, можно предсказать, в каком положении окажутся они через двадцать колебаний нижнего. Но никакими силами нельзя предсказать их положения через шестьдесят промежутков времени.

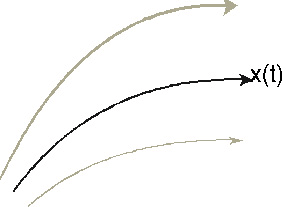
Рис. 2. Расходимость фазовых траекторий в системах с динамическим хаосом

Любая динамическая система определяет траекторию в фазовом пространстве, например, такую, как показана черной линией. Динамический хаос обусловлен тем, что соседние траектории, показанные бледными линиями, удаляются от нее. Из-за этого малые причины могут иметь большие следствия.

В 1963 году Рэй Брэдбери опубликовал фантастический рассказ, в котором фактически сформулировал идею динамического хаоса. В этом рассказе один из организаторов предвыборной кампании после победы своего кандидата отправляется в путешествие во времени. Фирма, организующая такую поездку, предлагает охоту на динозавров, которым в ближайшее время суждено умереть. Чтобы не нарушить сложную ткань причинно-следственных связей и не изменить будущее, следует двигаться по специальным тропам. Однако герой не смог выполнить этого условия и нечаянно раздавил золотистую бабочку. Возвратившись назад, он видит, что изменились состав атмосферы, правила правописания и итог предвыборной кампании. Едва заметное движение повалило маленькие костяшки домино, те повалили костяшки побольше, и, наконец, падение гигантских костяшек привело к катастрофе. Отклонения от исходной траектории, вызванные раздавленной бабочкой, стремительно нарастали (см. рис. 2). Малые причины имели большие следствия. Математики называют это свойство чувствительностью к начальным данным.

В том же 1963 году мысль о принципиальной ограниченности нашей способности предсказывать (или, как сейчас говорят, о существовании горизонта прогноза, или пределов предсказуемости) даже в мире, который идеально описывается классической механикой, была высказана лауреатом Нобелевской премии Ричардом Фейнманом. Для существования горизонта прогноза не нужно, чтобы "Бог играл в кости", добавляя в уравнения, описывающие нашу реальность, какие-то случайные члены. Не надо опускаться на уровень микромира, на котором квантовая механика дает вероятностное описание Вселенной. Объекты, поведение которых мы не можем предсказывать на достаточно большие времена, могут быть очень простыми. Например, такими, как представленный маятник.

То, что чувствительность к начальным данным ведет к хаосу, понял - и тоже в 1963 году - американский метеоролог Эдвард Лоренц. Он задался вопросом: почему стремительное совершенствование компьютеров, математических моделей и вычислительных алгоритмов не привело к созданию методики получения достоверных среднесрочных (на 2-3 недели вперед) прогнозов погоды? Эдвард Лоренц предложил простейшую модель, описывающую конвекцию воздуха (она играет важную роль в динамике атмосферы).

Эта модель описывается внешне очень простыми уравнениями[1]

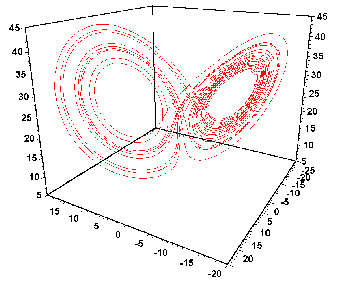
Рис. 3. Аттрактор Лоренца

Такая картина, полученная на компьютере (расчет проводился при r=28, s=10, b=8/3), убедила Э. Лоренца, что он открыл новое явление - динамический хаос. Этот клубок траекторий, называемый сейчас аттрактором Лоренца, описывает непериодическое движение с конечным горизонтом прогноза. где переменная x характеризует поле скоростей, y и z - поле температур жидкости. Здесь r = R/Rc, где R - число Рэлея, а Rc - его критическое значение; s - число Прандтля; b - постоянная, связанная с геометрией задачи. Компьютерный анализ системы Лоренца привел к принципиальному результату. Этот результат - динамический хаос, т.е. непериодическое движение в детерминированных системах (то есть в таких, где будущее однозначно определяется прошлым), имеющее конечный горизонт прогноза. Увиденное Лоренцем показано на рис. 3. С точки зрения математики, можно считать, что любая динамическая система, что бы она ни моделировала, описывает движение точки в фазовом пространстве. Важнейшая характеристика этого пространства - его размерность, или, попросту говоря, количество чисел, которые необходимо задать для определения состояния системы. С математической и компьютерной точек зрения не так уж и важно, что это за числа - количество рысей и зайцев на определенной территории, переменные, описывающие солнечную активность или кардиограмму, или процент избирателей, поддерживающих президента. Если считать, что точка, двигаясь в фазовом пространстве, оставляет за собой след, то динамическому хаосу будет соответствовать клубок траекторий. Например такой, как показан на рис. 3. Здесь размерность фазового пространства всего 3 (это пространство x, y, z). Замечательно, что такие удивительные объекты существуют даже в трехмерном пространстве. Для установившихся колебаний, соответствующих динамическому хаосу, Д. Рюэль и Ф. Такенс в 1971 году предложили название - странный аттрактор.

Пророчество Анри Пуанкаре о том, что в будущем можно будет предсказывать новые физические явления, исходя из общей математической структуры описывающих эти явления уравнений, компьютерные эксперименты превратили в реальность.

Система Лоренца имеет конечный горизонт прогноза. Почему? Можно пояснить это следующим образом. Если мы вновь возьмем две близкие траектории, показанные на рис. 3, то они расходятся, как на рис. 2. Одна уходит от второй. Скорость расходимости определяется так называемым ляпуновским показателем, и от этой величины зависит интервал времени, на который может быть дан прогноз. Можно сказать, что для каждой системы есть свой горизонт прогноза [2,3]. Развитие науки показывает, что каждая фундаментальная теория не только давала новые возможности, но и лишала нас иллюзий. Классическая механика лишила иллюзии, что можно построить вечный двигатель первого рода, термодинамика - второго, квантовая механика - что мы можем одновременно сколь угодно точно измерять координату микрочастицы и ее импульс. Теория относительности - что удастся передавать информацию в вакууме со сверхсветовой скоростью. Сегодня нелинейная динамика лишила нас иллюзии глобальной предсказуемости: мы не можем предсказать, начиная с какого-то горизонта прогноза, поведение многих достаточно простых систем и, в частности, этого маятника.

В свое время работа Лоренца была опубликована в метеорологическом журнале, но в течение 10 лет она не была замечена. Метеорологи сегодня полагают, что горизонт прогноза для погоды не превышает трех недель. Т.е. как бы точно мы сейчас ни промеряли параметры атмосферы, предсказать погоду с помощью имеющихся приборов через три недели в данном месте, вообще говоря, невозможно. Горизонт прогноза для состояния океана эксперты оценивают в месяц. Сейчас многие специалисты по физике Солнца предполагают, что аналогичная ситуация имеет место с Солнцем. Например, известно такое явление, как минимум Маундера, когда в течение почти 70-ти лет всплесков солнечной активности не было. И возникает вопрос, можем ли мы предсказать следующий минимум аналогичного сорта. Те работы, которые проводятся, показывают, что ляпуновские показатели таковы и горизонт прогноза таков, что этого предсказания на несколько десятилетий сделано быть не может.

Однако нелинейная динамика позволила увидеть не только принципиальные трудности, но и новые замечательные возможности. Обратим внимание на одну из них. Давайте посмотрим, сколько нужно чисел для того, чтобы описать эту систему, этот простейший маятник. Классическая наука говорит, что для того, чтобы описать этот маятник, чисел нужно бесконечно много. В самом деле, маятник, очевидно, подчиняется законам механики, но для того, чтобы такая игрушка вращалась и не останавливалась из-за трения, должно создаваться электромагнитное поле. Поэтому - механика плюс электродинамика, уравнения Максвелла. Формально бесконечно много степеней свободы.

Нелинейная динамика, анализируя системы такого сорта, позволяет устанавливать, сколько переменных необходимо для их описания, сколько переменных нужно для прогнозирования, она помогает выяснить, каким должен быть их мониторинг. Оказывается, что для такой системы нужно не более десятка переменных. Это открывает совершенно новые возможности. У нас есть формально очень сложная система и нам требуется выделить из нее самое главное. Если раньше, в 60-ые гг., был моден системный анализ, рассматривавший некие общие свойства систем, которые возникают у них, как у целого, то сейчас нам в Институте прикладной математики им. М.В. Келдыша РАН очень нравится слово системный синтез. Такой синтез позволяет из массы переменных извлечь именно то, что нужно для принятия решения.

После того, как было понято, что есть принципиальные ограничения в области прогноза, созданы новые поколения моделей и алгоритмов, прогноз стал индустрией. Сейчас происходит скачок в прогнозировании - скачок, который можно сравнить с тем, что произошло с наступлением эпохи персональных компьютеров. До персональных компьютеров ЭВМ были огромными и дорогими комплексами, которые были по силам только очень крупным фирмам. А после появления персональных компьютеров вычислительная техника стала доступна очень многим. Та же самая революция происходит сейчас в области прогнозов. Это перестало быть наукой, это становится технологией. Если раньше "РЭНД корпорейшн" и несколько других коллективов обеспечивали прогнозами правительство США и еще несколько ведомств, то сейчас даже не очень крупные фирмы имеют лаборатории, которые прогнозируют, лаборатории, как их называют, "проектирования будущего". Динамический хаос позволил в ряде случаев диагностировать серьезные заболевания по данным об электрической активности с помощью довольно простых компьютерных программ, предложить новые алгоритмы сжатия данных и защиты информации. Экономические прогнозы, опирающиеся на представления о хаосе и странных аттракторах, стали бурно развивающейся областью деятельности. Нельзя не вспомнить о "нелинейных журналах" - "Physica D", "Chaos", "Nonlinearity", "Physical Review E", "Прикладная нелинейная динамика" и многие другие. Оказалось, что есть гораздо больше того, что связывает объекты различных научных дисциплин, по крайней мере с точки зрения прогноза, чем того, что их разделяет.