ДИФФЕРЕНЦИАЛЬНАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЭВОЛЮЦИИ МЕТЕОПАРАМЕТРОВ

Климова Е.А., Беловодский В.Н.

Донецкий национальный технический университет г.Донецк

 

Источник: Информационные управляющие системы и компьютерный мониторинг — 2010 / Матеріали I всеукраинской научно-технической конференции студентов, аспирантов и молодых учёных. — Донецьк, ДонНТУ — 2010, с. 115-118.

 

Актуальность. Правильный прогноз погоды актуален независимо от времени и местности. С его помощью нельзя избежать природных катаклизмов (наводнений, ураганов, резких похолоданий), но можно предупредить об их появлении. А это может помочь сократить их возможные последствия – жертвы и материальные убытки. Данные прогноза погоды не менее важны и для сельского хозяйства, воздушного и морского транспорта, других областей человеческой деятельности.

В связи с прогрессом в области компьютерных технологий, появлением новых подходов используемых для прогнозирования, улучшением средств наблюдений и сбора данных возрастает возможность и для осуществления более точного прогноза.

Для осуществления прогнозирования погоды необходимо собрать информацию о состоянии погодных условий (влажности, температуре, атмосферном давлении, направлении ветра). Именно для этих целей используют метеостанции. Одна из таких метеостанций, Vantage Pro 2, расположена в ДонНТУ на факультете компьютерных наук и технологий. Она представляет собой беспроводную метеостанцию, которая измеряет следующие параметры: атмосферное давление, температуру, скорость и направление ветра, температуру точки росы, количество и интенсивность осадков, время захода и восхода солнца и ультрафиолетовое излучение.

Обзор предметной области исследования. Рассматриваемый подход основан на временных рядах – рядах значений метеовеличин. Их сбор ведется на метеостанциях. Одна из таких метеостанций установлена на кафедре КСМ, это метеостанция – Vantage Pro 2, которая с промежутком 10 минут фиксирует: температуру, давление, влажность, направление и скорость ветра.

В конечном счете прогнозирование по временному ряду сводится к задаче аппроксимации функции с помощью погружения ряда в многомерное пространство. Многомерное пространство образует множество операторов, которые, по сути, и представляют собой нейронную сеть, преобразуя входной сигнал в выходной. Теоретический фундамент этой методологии заложен теоремой Такенса ,которая гласит: если временной ряд порождается динамической системой, то есть значения X_t есть произвольная функция состояния такой системы, существует такая глубина погружения d (примерно равная эффективному числу степеней свободы данной динамической системы), которая обеспечивает однозначное предсказание следующего значения временного ряда. Таким образом, выбрав достаточно большое значение d , можно гарантировать однозначную зависимость будущего значения ряда от его d предыдущих значений: X_t=F(X_t-d)и предсказание временного ряда сводится к задаче интерполяции функции многих переменных.

Основным математическим аппаратом нелинейной динамики являются, как правило, дифференциальные уравнения. Именно на их основе, в данной работе, предполагается осуществлять прогноз, а именно, правые части этих уравнений описывать с помощью нейронных сетей.

Опыт показывает, что искусственные нейронные сети нередко оказываются более эффективными, чем классические методы прогнозирования. Они дают более точный результат и позволяют работать с зашумленными и неточными данными. Нейронная сеть не прогнозирует будущее, она пытается найти текущее состояние системы в раннее встречающихся ситуациях и максимально точно воспроизвести результат.

Анализ последних исследований. На кафедре КСМ в течение последних двух лет магистрами Гриценкой А.В и Сивяковым А.С. была разработана программная система Fcomplex, предназначенная для краткосрочного прогнозирования метеопараметров по временным рядам с использованием конечных математических моделей. Прогнозирование осуществляется на базе временных рядов, снимаемых с метеостанции Vantage Pro 2. Fcomplex - это программная система для составления краткосрочных прогнозов значений метеопараметров "Температура", "Давление", "Влажность" и "Скорость ветра" с заблаговременностью 1, 3, 6 и 9 часов. Для определения размерности модели в ней используются методы – главных компонент и ложных соседей, для построения аппроксимирующих зависимостей, – искусственные нейронные сети и метод Эглайса.

Обоснование и пути решения выделенных задач.В данной работе расчет прогноза предполагается проводить путем выполнения следующих этапов:

1. получение временного ряда из базы данных (БД), содержащей данные снимаемые с метеостанции Vantage Pro 2;
2. анализ данных;
3. определение размерности модели;
4. прогнозирование;
5. проверка эффективности модели.

Рассмотрим более подробно каждый этап.

Этап № 1. На этом этапе происходит получение временных рядов выбранной метеовеличины из БД, содержащей информацию, которая передается с метеостанции Vantage Pro 2 с временным интервал в 10 минут, по следующим показателям: температура, влажность, давление, скорость ветра.

Этап № 2. На этом этапе происходит предварительный анализ данных, а именно сглаживание с помощью скользящего среднего.

Обычно, сглаживание временного ряда осуществляется с целью уменьшения ошибки исходных данных, в частности – уменьшения случайного шума, полученного при измерении на метеостанции. По своей сути, сглаживание представляет собой, своего рода, усреднение в результате чего случайные составляющие в компонентах временного ряда взаимно поглощают друг друга.

С целью нахождения наилучшего метода сглаживания нами были проведены эксперименты по сглаживанию различных метеорядов. Было проведено экспоненциальное сглаживание временных рядов и сглаживание с использованием скользящей средней, а также, была вычислена средняя относительная ошибка сглаживания. Эксперименты показали, что средняя относительная ошибка при экспоненциальном сглаживании возрастает с увеличением длины временного ряда, и превышает среднюю относительную ошибку при сглаживании простым средним. На основании этого в дальнейшем предполагается использовать сглаживание скользящей средней.

Этап №3. На этом этапе определяется наименьшая размерность модели, обеспечивающую однозначность прогноза. Для решения этой задачи известны различные методы, – это, в частности: методы ложных соседей, главных компонент, Грассбергера- Прокаччиа, хорошо приспособленного базиса.

Для определения размерности модели в дальнейшем предполагается использовать метод Грассбергера-Прокаччиа. Метод Грассбергера-Прокаччиа был, выбрал потому, что первые два метода (методы ложных соседей, главных компонент) уже реализовывались на нашей кафедре в виде программной системы Fcomplex. А также потому, что одним из главных достоинств методы является простота реализации.

Метод Грассбергера-Прокаччиа является одним из самых распространенных для определения корреляционной размерности. Корреляционная размерность показывает число пар точек, достаточных для определения состояния динамической системы.

Для применения метода Грассбергера-Прокаччиа из одномерного временного ряда сначала следует получить многомерный, что можно сделать, используя идею метода запаздывания реконструкции аттрактора.

Для определения размерности модели вычисляется корреляционный интеграл C(e), показывающий относительное число пар точек аттрактора, находящихся на расстоянии, не большем e:

где Q – функция Хевисайда, т.е.

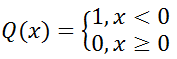
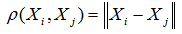– расстояние в m-мерном фазовом пространстве,

где N – число точек X_i на аттракторе.

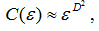
D₂– корреляционная размерность аттрактора.

Размерность определяется как тангенс угла наклона прямой, аппроксимирующей график корреляционного интеграла C(e) в двойном логарифмическом масштабе.

Этап № 4. На этом этапе формируется математическая модель процесса в виде дифференциального уравнения и осуществляется прогноз.

Ещё И.Ньютон писал: «Законы природы выражаются дифференциальными уравнениями». Именно, с помощью дифференциальных уравнений удается описывать эволюцию систем и прогнозировать ее поведение в следующие моменты времени. Дифференциальные уравнения являются основным математическим аппаратом нелинейной динамики, они применяются в качестве основного прогностического инструмента и в данной работе.

Именно поэтому для прогноза выбираются обыкновенные дифференциальные уравнения:

dx/dt=f(x,c)

где x – D-мерный вектор состояния, f – вектор – функция, с – Р-мерный вектор параметров, t – непрерывное время.

Определяется вид функций f с использованием метода сильной аппроксимации –искусственных нейронных сетей.

Нейронные сети «наиболее универсальный» способ аппроксимации функций многих переменных в том смысле, что он не только теоретически обоснован, но и успешно работает на практике. С использованием программной системы Fcomplex были проведены эксперименты с тремя видами сетей: линейной, нелинейной и регрессионной. Эксперименты показали, что наилучший прогноз для дальности прогнозирования 1, 3, 6, 9 часов дает нелинейная сеть.

В данном случае, нелинейная сеть представляет собой один скрытый слой (от 1 до 10 нейронов) с функцией активации гиперболического тангенса и выходным слоем, содержащим 1 нейрон с линейной функцией активации. На рисунке 1 представлена структура нелинейной сети.

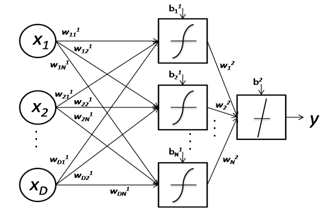
Рисунок 1 – Архитектура искусственной нейронной сети

Сеть не содержит обратных связей, нейроны соединяются по принципу «каждый с каждым». Оба слоя имеют смещения. Веса и смещения настраиваются методом Левенберга-Марквардта, критерий качества обучения – средняя квадратичная ошибка.

Математическое описание модели имеет вид:

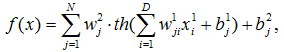
где параметром функции f является временной ряд x.

То есть, прогноз предполагается осуществлять с помощью модели:

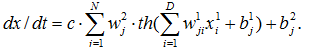
Этап №5. На этом этапе происходит проверка эффективности модели. Эффективность модели определяется её целями. Так как целью модели является прогноз метеопараметров, то лучшей проверкой эффективности будет сравнение полученных прогнозных значений с истинными значениями метеопараметров.

Выводы. В докладе описаны основные этапы работы, выполняемой в настоящее время, для формирования математической модели динамики метеопараметров, которая в дальнейшем предполагается для их экспериментального прогнозирования.

 

Список литературы

1. Б.П. Безручко, Д.А. Смирнов. Реконструкция обыкновенных дифференциальных уравнений по временным рядам. Саратов: ГосУНЦ «Колледж», 2000 – 48с.
2. Исследователь. [Electronic resourse] / Интернет-ресурс. – Режим доступа: http://ligis.ru/effects/stat/modules/sttimser.html – Анализ временных рядов.