• ДонНТУ
  • Портал магистров ДонНТУ

 

АЛГОРИТМ ЕВОЛЮЦІЇ МЕТЕОПАРАМЕТРІВ, НА ОСНОВІ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ

Климова К.О.

Керівник: к.т.н., доцент каф. КСМ Бєловодський В.М.

Донецький національний технічний університет

 

Источник: Современные Информационные Технологии 2011/ Материалы I Международной конференции студентов и молодых ученых. — Одесса, ОНПУ — 2011, с. 32-33.

 

Майже кожна людина слідкує за прогнозом погоди. Завдяки вірному прогнозу погоди можливо скоротити наслідки катаклізмів, якщо вчасно встигнути попередити людей про зміну стану погоди.

Зараз відбувається стрімкий ріст досліджень у галузі прогнозування метеопараметрів. Це пов’язано з прогресом у галузі комп’ютерних технологій, з появою нових підходів до прогнозування та покращення пристроїв спостереження та збору даних

У даній роботі прогноз передбачається вести шляхом виконання наступних етапів:

  1. Отримання часового ряду з бази даних Vantage Pro 2. На цьому етапі відбувається отримання часового ряду вибраного метеорологічного параметра з бази даних Vantage Pro 2.
  2. Аналіз даних. Попередній аналіз даних включає в себе згладжування часового ряду. Це робиться з метою зменшення помилки вихідних даних (випадкового шуму). По суті, згладжування являє собою усереднення даних, під час якого випадкові складові у компонентах часового ряду взаємно поглинають один одного.
  3. Визначення розмірності моделі. На цьому етапі визначається найменша розмірність моделі, яка б забезпечувала однозначність проноза. Для вирішення цієї задачі існує ряд методів, зокрема це метод помилкових сусідів, головних компонент, Грассбергера-Прокаччі, добре пристосованого базису. Надалі передбачається використовувати метод Грассбергера-Прокаччі. Одним з головних достоїнств цього методу є його простота реалізації.

    Для визначення розмірності моделі обчислюється кореляційний інтеграл C(е), що показує відносне число пар точок аттрактора, що знаходяться на відстані, не більшій е:

    де Q – функція Хевісайда, тобто

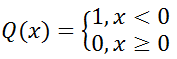
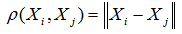    – в m-мірному фазовому просторі,

    где N – кількість точок Xi на аттракторі.

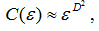
    D2– кореляційна розмірність аттрактора.

    Розмірність визначається як тангенс кута нахилу прямої, апроксимуючої графік кореляційного інтеграла C(е) в подвійному логарифмічному масштабі.

  4. Прогнозування. На цьому етапі формується математична модель процесу у вигляді диференціального рівняння і здійснюється прогноз. Для прогнозу вибираються звичайні диференціальні рівняння:

    dx/dt=f(x,c)

    де x – D-мірний вектор стану, f – вектор-функція, с – Р-Р-мірний вектор параметрів, t – час.

    Вид функцій f визначається з використанням методу сильної апроксимації – штучних нейронних мереж. Нейронні мережі «найбільш універсальний» спосіб апроксимації функцій багатьох змінних в тому сенсі, що цей метод не тільки теоретично обґрунтований, але й успішно працює на практиці. З використанням програмної системи Fcomplex були проведені експерименти з трьома видами мереж: лінійної, нелінійної та регресійної. Експерименти показали, що найкращий прогноз для дальності прогнозування 1, 3, 6, 9 годин дає нелінійна мережа.

    Мережа не містить зворотних зв'язків, нейрони з'єднуються за принципом «кожен з кожним». Обидва шари мають зміщення. Вага та зміщення настроюються методом Левенберга-Марквардта, критерій якості навчання – середня квадратична помилка. Математичний опис моделі має вигляд:

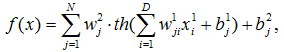
    Тобто, прогноз передбачається здійснювати за допомогою моделі:

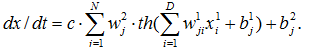
  5. Перевірка ефективності моделі. Ефективність моделі визначається її цілями. Оскільки метою моделі є прогноз метеопараметрів, то найкращою перевіркою ефективності буде порівняння отриманих прогнозних значень з істинними значеннями метеопараметрів.

Можна зробити висновок, що прогнозування є дуже актуальною тему у будь-якому регіоні. А також, що прогнозування на основі нейронних мереж є одним з найточніших методів (зокрема на основі нелінійної мережі). Тому, що нейронні мережі дають більш точний результат, ніж класичні методи прогнозування і дозволяють працювати з неточними даними.

 

Список литературы

  1. Б.П. Безручко, Д.А. Смирнов. Реконструкция обыкновенных дифференциальных уравнений по временным рядам. Саратов: ГосУНЦ «Колледж», 2000 – 48с.
  2. Исследователь. [Electronic resourse] / Интернет-ресурс. – Режим доступа: http://ligis.ru/effects/stat/modules/sttimser.html – Анализ временных рядов.