Оценка размерности аттракторов погоды и климата: процедура и интерпретация
Авторы: A.A.Tsonis
Department of Geosciences, University of Wisconsin - Milwaukee, Milwaukee, Wisconsin
J.B. Elsner
Department of Meterology, The Florida State University, Tallahassee, Florida
K.P.Georgakakos
Department of Civil and Envirinmental Engineering and Iowa Institute of Hydraulic Research, The University of Iowa, Iowa City, Iowa
Автор перевода: Климова Е.А.
Источник: http://journals.ametsoc.org/doi/pdf/10.1175/1520-0469(1993)050%3C2549%3AETDOWA%3E2.0.CO%3B2
Резюме. При реконструкции аттракторов из наблюдаемых значений часто используется алгоритм Грассбергера-Прокаччиа для оценки корреляционной размерности. В данной работе приведен обзор последних исследований касающихся требований к данным и алгоритму. В свете этих исследований обсуждается оценка размерности аттракторов погоды и климата.
1.Введение
В последнее время идеи теории нелинейных динамических систем и хаоса были применены для многих задач во многих различных дисциплинах, включая науку об атмосфере. Основная цель – поиск минимальной размерности хаоса и определение свойств аттракторов, если таковые имеются. Эта процедура часто включает в себя наблюдаемые (временные ряды) и реконструкцию аттрактора. Реконструкция достигается путем взятия скалярного временного ряда x(ti) и последовательных сдвигов времени (задержек) в виде векторного временного ряда:

Где n - размерность вектора X(ti) (часто называемая размерностью вложения),а τ - временная задержка (Раркард, Такенс, Руль). Для правильной реконструкции размерность вложения n должна быть равна или больше 2D+1, где D – размерность многообразия содержащего аттрактор. Такие вложения сохраняют топологические свойства аттрактора. Более конкретно вложение будет диффеоморфизмом - дифференцируемое отображение из фазового пространства в пространство запаздывания. Это теорема Уитни, она строга говоря, справедлива только тогда, когда имеется бесконечное множество. Когда мы имеет ограниченный набор данных, теорема может быть не справедлива. Фактичекси, в этом случае, вложение используется свободно.
Для n-мерного фазового пространства будет наблюдаться множество точек. Для такого множества при различных размерностях и показателях характеристик аттрактор может быть определен. Наиболее популярный метод для расчета корреляционной размерности – это метод Грассбрегера-Прокаччиа. В соответствии с этим методом (Грассбрегера-Прокаччиа, 1983) для множества точек можно найти количество пар N(r,n) с расстоянием между точками меньше r. В этом случае, для малых r мы определяем, что
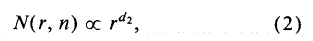
Где скалярный показатель d - это корреляционная размерность аттрактора для данного n. Так как размерность аттрактора неизвестна используя уравнение (2) определяем значение насыщенное D2, для разных значений n, которое будет использовано для оценки корреляционной размерности аттрактора. Для более подробного ознакомление с вышеупомянутой процедурой и приложениями связанными с погодой и климатом обратитесь к статьям Tsonis и Elsner (1989, 1990).
Этот доклад обсуждает три важных вопроса касающихся вышеупомянутой процедуры: 1) Выбор τ; 2) Достаточное количество точек; 3) Что означают результаты?
1. Выбор τ
Когда мы реконструируем аттрактор, точки, которые используется для определения размерности вложения, должны быть независимы друг от друга. В противном случае x(t+τ) =x(t) и точки как правило размещаются на диагонали. Результат оценки корреляционно размерности может быть не объективным (обычно, недооцененным). Поэтому, τ должен быть выбран так, чтобы точки, не коррелировали с ранее созданными точками. Итак, τ должен быть выбран как декорреляционное время. Возникает вопрос: как мы определим время декорреляции? Простая процедура определения декорреляционного времени равного лагу автокорреляционной функции, когда тот первый раз достигает нуля. Другие методы определения лага, когда АКФ достигает определенных значений, таких как 1/е, 0.5, или 0.1. Как было отмечено, однако, Frazer и Swinney автокорреляционная функция является мерой линейной зависимости между последовательными точками и может быть использована когда мы имеет дело с нелинейной динамикой. Они доказали, что в качестве τ должна быть использована взаимная информация, меры основной зависимости между последующими точками. Очевидно, что не одно из вышеупомянутых правил не является бесспорным правилом для выбора τ. Тем не менее, существуют очень обнадеживающие практические эксперименты по выбору τ. Обратите внимание, что в большинстве (если не во всех) исследованиях аттракторов погоды и климата был сделан выбор в пользу определения τ с помощью автокорреляционной функции.
2. Достаточное количество точек
На рисунке 1 показана корреляционная размерность как функция от размерности вложения для данных количества осадков (временной ряд delta(t(s))) между последовательными измерениями, каждому из которых соответствует значение 0,01 мм осадков. Здесь расчет D2 - наибольшей размерности вложения, не будет достигнут путем последовательного сдвига одного временного ряда с параметром задержки, но может быть достигнут путем введения нового события размером 2200 (то есть независимого временного ряда некоторого метерологического характера) каждый раз когда мы увеличиваем размерность вложения. Итак, наблюдаемые точки в d-мерном пространстве независимы и необходимо определить подходящую τ.
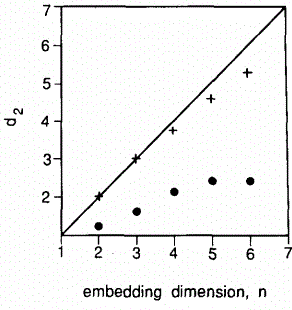
Рисунок 1 –корреляционная размерность D2 как функция от размерности вложения n для (а) данных представляющих ливневые осадки (точки) и (b) случайной выборки (крестики)
Какое необходимое число точек N для получения размерности вложения?
Расчеты для определения минимального числа точек первым сделал Smith (1988), который сделал вывод, что это количество равно 42m , где m наименьшее целое больше размерности объекты. Итак, если m=4, для получения точной оценки D2, N по крайней мере должен быть равен 3 111 696 . На самом деле, результаты Smith убили все надежды для оценки размерности аттрактора независимо от доступности данных, поскольку даже суперкомпьютеры не могут справиться с такой задачей. Но точная оценка для m=4 может быть получена с использованием 5000 точек. Это число значительно ниже, чем 3 111 696. Откуда такое несоответствие? Единственное объяснение, что 42m это ошибка. В самом деле, было недавно доказано, что процедура Smith получена оценки как 42m является недействительной. На самом деле, минимальное число точек необходимых для получения размерности вложения Nmin должно быть не более А (обычно А= 0,05n), и определяется как:

где n – размерность вложения и Г(х) – это гамма функция. Параметр k определяется как ширина интервала масштабирования. Напомним, что d2 оценивается как отношения d2=[lnC(r')-lnC(r)]/[ln(r')-ln(r)]. Тогда параметр k определяется как k=r'/r. Для использования на практике А= 0,05n и для k=4 уравнение (3) может быть приближено (для n<20) как
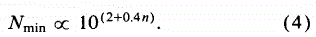
Итак, для n=4, Nmin=103.6=4000 как уже упоминалось выше.
Вышеупомянутое обсуждение неизбежно подводит нас к следующему очень важному моменту. Основные предположения о необходимости числа точек в зависимости от размерности вложения представленные до этого момента действительны только до тех пор, пока вложение размерности n меньше корреляционной размерности D.
Кроме того, вполне возможно, оценка числа точек будет зависеть от типа аттрактора. Недавно, Лоренц рассмотрел три переменные хаотической системы и создал модель, взяв семь линейно связанных копий этой системы. Модель описывается 21 уравнением и её размерность равна 17.
Лоренц применяет алгоритм Грассбергера-Прокаччиа с использованием 4000 значений выбранной переменной из модели.
Он обнаружил, что если N не слишком велико, то алгоритм недооценивает размерность. Однако: 1) различные переменные могут давать различные оценки, и 2) соответствующие переменные могут давать довольно хорошую оценку.
Такие переменных сильно связаны с остальной частью переменных модели. Если это утверждение верно для всех хаотических систем, то мы должны беспокоиться не о размере выборки, а об выборе наблюдаемых!
Помимо этих важных вопросов, не известно, на данный момент или нет (и особенно для фрактальных множеств) как потребность в данных увеличивается, когда n>D2.
Эксперименты с известными динамическими системами показывают, что в этом случае, хотя потребность в данных может увеличиться она не может быть столь серьезной, как это предсказывается вышеупомянутые формулы!
Например, рисунок 2 показывает наклон логарифмического участка ряда размером 2000 для наблюдаемой с карты Хенона с размерностью вложения 2, 3, 4, 5, 6 7 и 8. Заметим, что при n= 2, d2 =1,25.
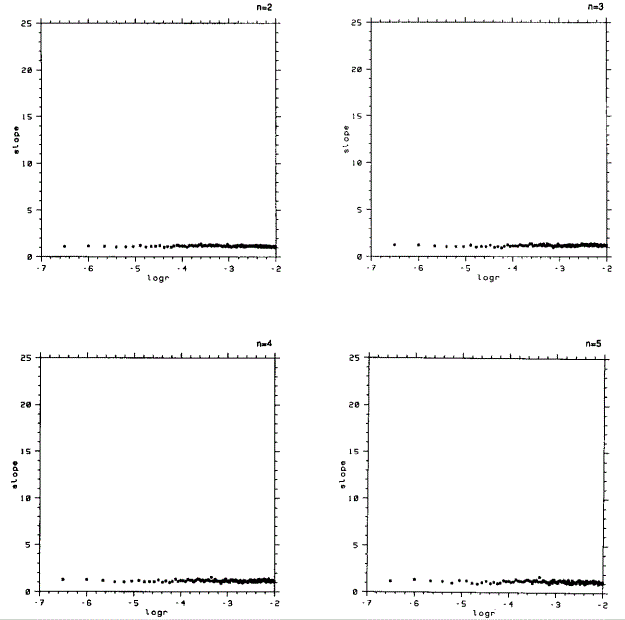
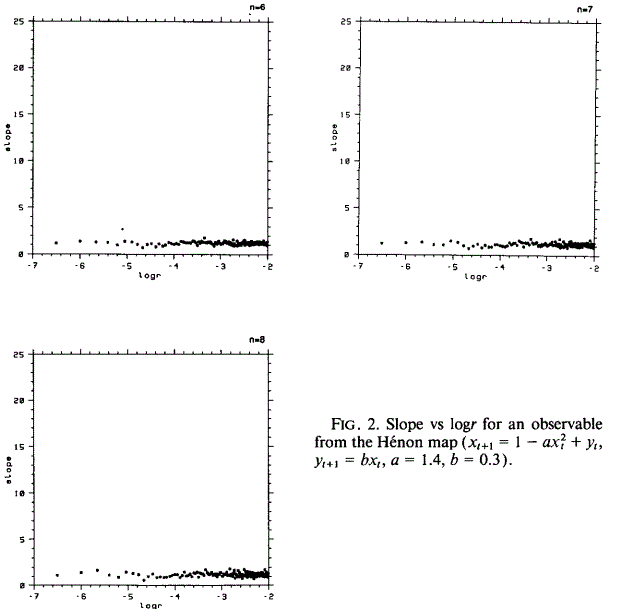
Впоследствии, заметим, что могут быть получены достаточно точные оценки корреляционной размерности для размерности вложения равной 8. В самом деле, мы не наблюдаем слишком большое колебание или недооценку D2 с ростом размерности вложения.
Аналогичные результаты получены и для других динамических систем, таких как логистического отображения и системы Лоренца. Данные, используемые на рисунке 1 - похожая история, но по сравнению с наклоном логарифмических кривых показывают больший разброс из-за наличия шума в реальных данных. Эти результаты обеспечивают некоторое свидетельство, что для фрактальных множеств потребность в данных может увеличиться гораздо более медленными темпами.
3.Что означает конечная размерность?
Вернемся к рисунку 1, теперь мы можем представить какой результат получается, если в расчетах используется случайная выборка размером 2200. Эти результаты свидетельствуют, что существует большая разница между случайной выборкой и данными об осадках. Случайные выборки моделируются так, что они имеют схожие статистические свойства (например, распределение вероятностей, спектров и т.д.) с фактическими данными и часто упоминаются в качестве суррогатных данных. Обеспечивает ли рисунок 1 убедительные доказательства, что существует основной аттрактор в данных об осадках? Важность этого вопроса заключается в том, что с учетом конечной корреляционной размерности странного аттрактора, следует, что обратное утверждение не может быть правдой. Как многие утверждают, не существует теоремы, которая бы утверждала, что корреляция данной системы конечной размерности связана со странным аттрактором!
Когда алгоритм Грассбергера-Прокаччиа применяется к траектории реконструированной из одной последовательности с помощью метода задержки, получается конечная размерность (близкой к фрактальной размерности). Таким образом, они пришли к выводу, что конечное значение для корреляционной размерности не может свидетельствовать о динамической системе с конечным числом степеней свободы.
Она может только указать нижнюю границу для фактического числа степеней свободы, которое может быть бесконечным!
Мы должны отметить, что понятие фрактальной размерности может быть применено к временным рядам двумя различными способами. Во-первых, указать число степеней свободы лежащих в основе динамической системы. Во-вторых заключается в количественном самоподобии траектории в фазовом пространстве. Алгоритм Грассбергера-Прокаччиа используется для первого случая. Например, после применения алгоритма к наблюдаемым из системы Лоренца результаты в измерении были равны 2,07. Это значение не имеет ничего общего с самоподобия траектории Лоренца.
Литература
Benettin, G., D. Casati, L.Galgani, A.Giolgilli, and L,Sironi, 1986: Apparent fractal dimension in conservative dynamical systems. Phys.Lett.,118A, 325-330.
Bishop, A.R., and P.S. Lomdahl, 1986: Nonlinera dynamics in damped sine-Gordon systems. Physica, 18D, 54-66.
Bishop, A.R., M.G. Forest, D.W. McLaughlin, and E.A. Overman, 1986: A quasi-periodic route ti chaos in near-integrable PDE. Physica, 23D, 293-328.
Chernico, A.A., R.Z. Sagdeev, D.A. Usikov, and G.M.Zavlasky, 1989: SOv. SCi. REv. C. Math. Phys., 8, 83-172.
Elsner, J.B., and A.A.Tsonis, 1992: Nonlinear prediction, chaos and noise. Bull.Amer.Meteor.Soc., 73, 49-60.
Essex, C., and M.A.H.Nerenberg, 1991: "Comments on "Determinisitic chaos: The science and the fiction." Proc.R.Soc.London A., 453, 287-292.
Essex, C., T. Lookman, and M.A.Nerenberg, 1987 : The climate attractorover short time scales. Nature, 326, 64-66.
Fraedrich, K., 1986: Estimating the dimension of weather and climate attractors.J. Atmos.Sci., 43, 419-432.
Fraedrich, K., 1987: Estimating weather and climate predictability on attractors. J.Atmos. Sci., 44, 722-728.
Frazer, A.M., and H.L. Swinney, 1986: Independent coordinates for strange attractors from mutual information. Phys. Rev. A, 33, 1134-1140.
Grassberger, O., 1986: Do climate attractors exits? Nature, 323, 609-612.
Grassberger, O., and I.procaccia, 1983a:Characterization of strange attractors. Phys. Rev. Lett., 50, 346- 349.
Grassberger, O., and I.procaccia, 1983b: Measuring the strangeness of strange attractors. Physica, 9D, 189-208.
Keppenne, C.L., and C. Nicolis, 1989: Global properties and local structure of the weather attractors over Western Europe, J.Atmos. Sci., 46, 2356-2370.
Lorenz, E.N., 1991: Dimension of weater and climate attractors. Nature, 353, 241-244.
Mandelbrot, B.B., 1983: The Fractal Geometry of Nature. reeman, 461 pp.
Nerenberg, M.A.H., and C.Essex, 1990: Correlation dimension and systematic effects. Phys. Rev. A, 42, 7065-7074.
Nicolis, C., and G. Nicolis, 1984: Is there a climatic attractor? Nature, 331, 529- 532.
Osborne, A. R., and A. Provenzale, 1989: Finite correlation dimension for stochastic systems with power-law spectra. Physica D, 35, 357-381.
Osborne, A. R., and R. Caponio, 1990: Fractal trajectories and anomalous diffusion for chaotic motions in 2D turbulence. Phys. Rev. Lett., 64, 1733-1736.
Osborne, A. R., and A. D. Kirwan, Jr., A. Provenzale, and L. Bergamasco, 1986: A search for a chaotic behavior in large and mesoscale motions in the Pacific Ocean. Physica, 23D, 75-83.
Parcard, N.H., J.P.Farmer, and R.S. Shaw, 1980: Geometry from a time series. Phys. Rev. Lett., 45, 712-716.
Ruelle, D., 1981: Chemical kinetics and differentiable dynamical systems. Nonlinear Phenomena in Chemical Dynamics, A. Pacault and C. Vidal, Eds., Springer-Verlag.
Ruelle, D., 1990: Deterministic Chaos: The science and the fiction. Proc. Roy. Soc. London, A427, 241-248.
Schuster, H.G., 1988: Deterministic Chaos. VCH Weinheim, 122.
Sharifi, M.B., K.P. Georgakakos, and I.Rodriquez-iturbe, 1990: Evidence of deterministic chaos in the pulse of storm rainfall. J.Atmos.Sci., 47, 888-893.
Smith, L.A., 1988: Intrinsic limits on dimension calculation. Physics Lett. A., 133, 283-288.
Sugihara, G., and R.M. May, 1990: Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature. 344, 734 - 741.
Takens, F., 1981: Dynamical Systems and Turbulence. Lecture Notes in Mathematics 898. stringer-Verlag.
Theiler, A.A., 1991: Some comments on the correlation dimention of 1/fa noise. Phys. Lett. A, 155, 488-492.
Tsonis, A.A., and J.B. Elsner, 1988: The weather attractor over very short time scales. Nature, 33, 545-547.
Tsonis, A.A., and J.B. Elsner, 1989: Chaos strange attractor and weather. Bull. Amer. Meteor. Soc., 70, 16-23.
Tsonis, A.A., and J.B. Elsner, 1990: Comments on "Dimension analysis of climatic data." J.Climate, 3,1502-1505.
Tsonis, A.A., and J.B. Elsner, 1992: Nonlinear prediction as a way of distinguishing chaos from ramdom fractal sequences. Nature, 358, 217-220.