Библиотека по теме магистерской работы

РОЗРОБКА ТА ДОСЛІДЖЕННЯ ДВОХПРОЦЕСОРНОЇ СИСТЕМИ НА БАЗІ ПЛІС, ДОСЛІДЖЕННЯ ЇЇ РОБОТИ ЗА ДОПОМОГОЮ КІЛЬЦЕВОГО ТЕСТУ

Стародубцев Д.М., Кушнаренко В.Г.
Донецький національний технічний університет, кафедра комп’ютерної інженерії
Донецьк

Анотація

Стародубцев Д.М., Кушнаренко В.Г. Розробка та дослідження двохпроцесорної системи на базі ПЛІС, дослідження її роботи за допомогою кільцевого тесту. Спроектовано архітектуру та відлагоджено двохпроцесорну систему на базі ПЛІС. Розроблено алгоритм та реалізовано програму кільцевого тесту для відлагоджувальної плати XilinxSpartan 3EStarterKit (S3E). Проведено тестування паралельної роботи процесорів системи за допомогою кільцевого тесту.

Вступ

Останнім часом ПЛІС стали дуже поширеними у промисловості. Цей успіх пов’язаний з тим, що вони дають змогу створити майже будь-який пристрій. До системи, яку потрібно реалізувати, можуть входити всілякі нестандартні модулі, як програмні, так і апаратні. Такі комплекси дуже легко розробляються за допомогою великої кількості існуючих САПР.

Крім того, за допомогою ПЛІС можна розробляти і багатопроцесорні системи, що виконуватимуть які-небудь специфічні розрахунки. Дослідженню цієї проблеми і присвячена ця доповідь. Для цього було спроектовано двохпроцесорну систему на ПЛІС, розроблено алгоритм та реалізовано програму кільцевого тесту для неї, і досліджено роботу обчислювального комплексу.

Проектування архітектури двохпроцесорного комплексу на базі ПЛІС

У якості відлагоджувальної плати було обрано Xilinx Spartan 3E Starter KIT (S3E) [1]. Це плата середнього класу, яка має у своєму складі два вбудовані мікропроцесори MicroBlaze та засоби для їх програмування.

Для рішення поставленої задачі було розроблено архітектуру, зображену на рисунку 1.

Розробка системи виконувалась у САПР проектування ПЛІС Xilinx EDK. Отже, система складається з наступних компонент:

1. Два мікропроцесори MicroBlaze, які є основою всієї системи, і виконують розрахунки тесту.
2. Дві магістральні шини для кожного процесору (mp_plb). До цих шин під’єднуються всі інші пристрої, що використовуються кожним MicroBlaze.
3. Два елементи BRAM. Це модулі блочної пам’яті, які безпосередньо використовують процесори Microblaze для своїх потреб під час роботи.
4. Також у склад кожного процесору введено механізми для взаємодії з пам’яттю BRAM. Цей тип пам’яті є двонаправленим, тому механізмів для кожного процесору також два: механізм роботи з даними (dlmb) та механізм роботи з командами (ilmb).
5. Контролери роботи з процесором для BRAM. На кожний інтерфейс, який під’єднується до процесора, встановлено контролер, який буде керувати пересиланням та прийомом даних від процесора до пам’яті і навпаки (ilmb_cntlr та dlmb_cntlr).

Рисунок 1 – Функціональна схема двохпроцесорної системи на ПЛІС

6. Mailbox. Додано до системи всі елементи цього механізму передачі даних, бо він використовується для зв’язку між процесорами. Він під’єднується до кожної магістральної шини процесорів.
7. Механізм роботи з послідовним портом RS232. Він використовується для виводу і під’єднується тільки до шини першого процесору, бо тільки він виконує передачу даних до персонального комп’ютера.
8. Блок пам’яті DDR SDRAM. Він з’єднаний з обома шинами процесорів. Цей блок використовується для зберігання програм тесту та інших потреб під час обчислень.

Розробка алгоритму та реалізація програми кільцевого тесту

Кільцевий тест призначений для перевірки швидкодії обробки даних двох процесорної системи на ПЛІС [4]. Його зміст полягає у наступному. Програма кільцевого тесту розв’язує диференціальне рівняння генератора синусоїдальної функції:

=                                                                                                          (1)
де x =,
 – кругова частота функції,
 – початкова фаза,
 –  незалежна змінна, час.

Початкові умови: , .

Послідовно збільшуючи значення частоти, можна визначити максимальну частоту обробки сигналу такого типу двохпроцесорною системою на ПЛІС.

Для реалізації тесту на платі необхідно переписати рівняння (1) у вигляді системи рівнянь першого порядку.

Необхідно ввести позначення: .

Тоді  і рівняння (1) перетворюється в систему:

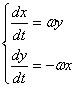                                                               (2)

Початкові умови мають наступний вигляд:

                                                         (3)
                                                        (4)

Інтегрувати систему (2) можна на двохпроцесорному вирішувачі, причому кожному з процесорів відводиться інтегрування одного рівняння з ідентичними правими частинами. Це забезпечує рівномірність завантаження процесорів.

Передача даних між рівняннями (і між процесорами) здійснюється за допомогою технології MailBox, яку підтримує плата.

Застосовуючи метод Рунге-Кутта, необхідно записати дискретну Simulations Model для задачі (2), (3), (4):

,            (5)
,            (6)

де Kj коефіцієнти обчислюються за формулами (7) та (8). При .

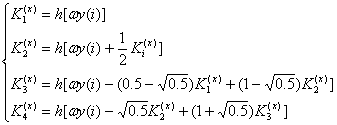                                  (7)
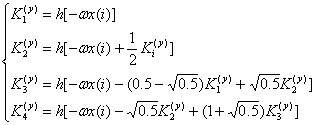                                      (8)

З використанням методу Ейлера рівняння мають наступний вигляд:

  ,                                                          (9)

при чому , .

З використанням методу Адамса-Башфорта системи рівнянь мають наступний вигляд:

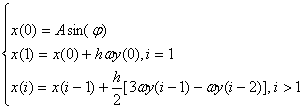                                (10)

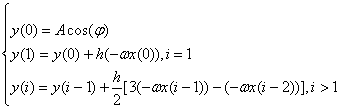                          (11)

Структурну схему генерування синусоїдальної функції наведено на рисунку 2.

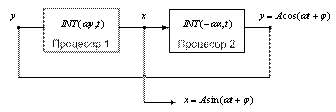
Рисунок 2 – Схема генерування синусоїдальної функції

Безперервна функція  квантується інтервалом часу Т, який зумовлюється сумарною тривалістю операцій в обох процесорах:

,

де – час виконання операції інтегрування, – час операцій обміну даними між процесорами.

З огляду на рівномірність завантаження процесорів обчисленнями за формулами обраних чисельних методів та  однаковість операцій обміну взято подвоєну суму цих часових інтервалів.

Фізично інтервал Т зумовлює ступеневу апроксимацію функції . Похибка цієї апроксимації буде дорівнювати , де  .

Рисунок 3 – Апроксимація функції

Аналіз показує, що . В зв’язку з тим, що для малих аргументів , можна прийняти:

.

Відносна похибка буде дорівнювати:

Для генерування синусоїди з відносною похибкою 0,1% на заданій частоті  необхідно забезпечити процесорний інтервал квантування

Навпаки, для фізично наявного інтервалу Т даний двохпроцесорний комплекс здатен генерувати синусоїду з частотами в межах

.

Практичну цінність має експеримент, в якому необхідно:

1. для фіксованого значення 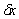 і невідомої величини Т експериментально визначити діапазон  ;
2. При фіксованих 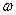 та  обчислити Т.

Мовою реалізації алгоритму було обрано С, бо саме вона підтримується платою.

Створену програму алгоритму кільцевого тесту було перевірено за допомогою бібліотеки MPI, а потім інтегровано у програмне забезпечення ПЛІС.

Останнім кроком було – дослідження роботи створеного обчислювального пристрою. Для цього частота синусоїди була обрана змінним параметром системи. Саме з її допомогою і досліджувалась швидкість роботи плати. У програмі встановлювались різні значення частоти. Потім розраховувався сигнал, і його координати виводились на термінал персонального комп’ютера.

Отримані результати зберігались у файл, який потім зчитувався програмою візуалізації. А вона вже будувала отриманий графік та еталонну синусоїду для заданих параметрів синусоїди (амплітуда, частота). Отримані результати зображено на   рисунку 4.

На наведених графіках еталонний сигнал зображено червоним кольором, а графік від плати – чорним. Вісь абсцис – це час, а вісь ординат – амплітуда сигналу.

Як бачимо, програма кільцевого тесту правильно розраховує значення сигналу, але із збільшенням частоти сигналу похибка у розрахунках стає досить великою, бо інтервал дискретизації досить малий. І тому лише перші  три результати можна рахувати біль-менш задовільними. В інших варіантах отриманий сигнал дуже відрізняється від еталонного.

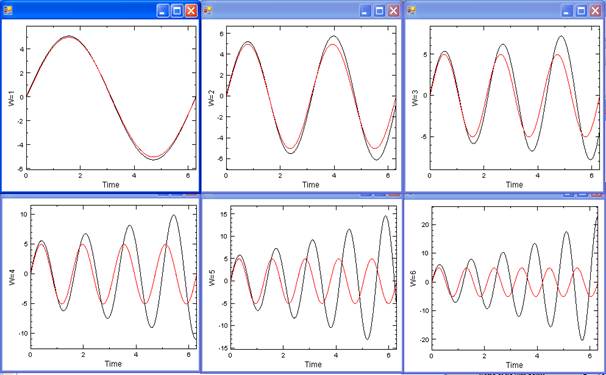
Рисунок 4 – Результати роботи тесту

Висновки

Розроблено обчислювальний комплекс на базі стаціонарного комп’ютера та двохпроцесорної системи на базі ПЛІС Xilinx Spartan 3E Starter Kit. Проведено дослідження його роботи у якості паралельного обчислювального комплексу. Отримані результати дають уявлення про швидкість роботи обраної плати. Для підвищення якості роботи розробленої системи можна використовувати наступні методи:

1. Обрати більш точний метод чисельного інтегрування.
2. Зменшити інтервал дискретизації шляхом розробки апаратного блоку інтегрування для системи.

Література

1. Spartan 3E Starter Kit Board User Guide / FPGA and CPLD Solutions from Xilinx, Inc. – Режим доступу: http://www.xilinx.com/support/documentation/boards_and_kits/ug230.pdf.
2. Метод Рунге-Кутта решения дифференциальных уравнений и их систем / DelphiPlus.org – Режим доступу: http://www.delphiplus.org/articles/algorithm/rk_method/index.html.
3. Asokan V. Designing Multiprocessor Systems in Platform Studio / FPGA and CPLD Solutions from Xilinx, Inc. – Режим доступу: http://www.xilinx.com/support/documentation/white_papers/wp262.pdf.
4. Святный В.А., Гибридные вычислительные системы [Текст]/ В. А. Святный// Учеб. пособие для вузов по спец. "Электрон. вычисл. машины". – Киев: Вища школа, 1980. – С. 103-117.