Terrain Rendering Using GPU-Based Geometry Clipmaps

Terrain Rendering Using

GPU-Based Geometry Clipmaps

by Arul Asirvatham, Hugues Hoppe

Revised April 2005

Source of information: http://http.developer.nvidia.com/GPUGems2/gpugems2_chapter02.html

The geometry clipmap introduced in Losasso and Hoppe 2004 is a new level-of-detail structure for rendering terrains. It caches terrain geometry in a set of nested regular grids, which are incrementally shifted as the viewer moves. The grid structure provides a number of benefits over previous irregular-mesh techniques: simplicity of data structures, smooth visual transitions, steady rendering rate, graceful degradation, efficient compression, and runtime detail synthesis. In this chapter, we describe a GPU-based implementation of geometry clipmaps, enabled by vertex textures. By processing terrain geometry as a set of images, we can perform nearly all computations on the GPU itself, thereby reducing CPU load. The technique is easy to implement, and allows interactive flight over a 20-billion-sample grid of the United States stored in just 355 MB of memory, at around 90 frames per second.

Review of Geometry Clipmaps

In large outdoor environments, the geometry of terrain landscapes can require significant storage and rendering bandwidth. Numerous level-of-detail techniques have been developed to adapt the triangulation of the terrain mesh as a function of the view. However, most such techniques involve runtime creation and modification of mesh structures (vertex and index buffers), which can prove expensive on current graphics architectures. Moreover, use of irregular meshes generally requires processing by the CPU, and many applications such as games are already CPU-limited.

The geometry clipmap framework (Losasso and Hoppe 2004) treats the terrain as a 2D elevation image, prefiltering it into a mipmap pyramid of L levels as illustrated in Figure 2-1. For complex terrains, the full pyramid is too large to fit in memory. The geometry clipmap structure caches a square window of nxn samples within each level, much like the texture clipmaps of Tanner et al. 1998. These windows correspond to a set of nested regular grids centered about the viewer, as shown in Figure 2-2. Note that the finer-level windows have smaller spatial extent than the coarser ones. The aim is to maintain triangles that are uniformly sized in screen space. With a clipmap size n = 255, the triangles are approximately 5 pixels wide in a 1024x768 window.

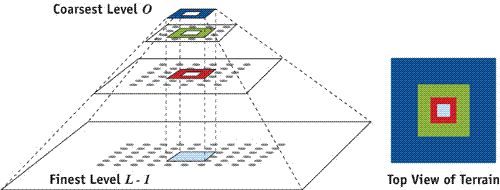
Figure 2-1 How Geometry Clipmaps Work

Figure 2-2 Terrain Rendering Using a Coarse Geometry Clipmap

Only the finest level is rendered as a complete grid square. In all other levels, we render a hollow "ring," which omits the interior region already rendered at finer resolutions.

As the viewer moves, the clipmap windows are shifted and updated with new data. To permit efficient incremental updates, the clipmap window in each level is accessed toroidally, that is, with 2D wraparound addressing (see Section 2.4).

One of the challenges with the clipmap structure is to hide the boundaries between successive resolution levels, while at the same time maintaining a watertight mesh and avoiding temporal popping artifacts. The nested grid structure of the geometry clipmap provides a simple solution. The key idea is to introduce a transition region near the outer perimeter of each level, whereby the geometry and textures are smoothly morphed to interpolate the next-coarser level (see Figure 2-3). These transitions are efficiently implemented in the vertex and pixel shaders, respectively.

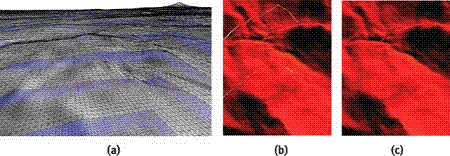
Figure 2-3 Achieving Visual Continuity by Blending Within Transition Regions

The nested grid structure of the geometry clipmap also enables effective compression and synthesis. It allows the prediction of the elevation data for each level by upsampling the data from the coarser level. Thus, one need only store or synthesize the residual detail added to this predicted signal.

Overview of GPU Implementation

The original implementation of geometry clipmaps presented in Losasso and Hoppe 2004 represents each clipmap level as a traditional vertex buffer. Because the GPU currently lacks the ability to modify vertex buffers, that implementation required significant intervention by the CPU to both update and render the clipmap.

In this chapter, we describe an implementation of geometry clipmaps using vertex textures. This is advantageous because the 2D grid data of each clipmap window is much more naturally stored as a 2D texture, rather than being artificially linearized into a 1D vertex buffer.

Recall that the clipmap has L levels, each containing a grid of nxn geometric samples. Our approach is to split the (x, y, z) geometry of the samples into two parts:

The (x, y) coordinates are stored as constant vertex data.

The z coordinate is stored as a single-channel 2D texture—the elevation map. We define a separate nxn elevation map texture for each clipmap level. These textures are updated as the clipmap levels shift with the viewer's motion.

Because clipmap levels are uniform 2D grids, their (x, y) coordinates are regular, and thus constant up to a translation and scale. Therefore, we define a small set of read-only vertex and index buffers, which describe 2D "footprints," and repeatedly instance these footprints both within and across resolution levels, as described in Section 2.3.2.

The vertices obtain their z elevations by sampling the elevation map as a vertex texture. Accessing a texture in the vertex shader is a new feature in DirectX 9 Shader Model 3.0, and is supported by GPUs such as the NVIDIA GeForce 6 Series

Storing the elevation data as a set of images allows direct processing using the GPU rasterization pipeline. For the case of synthesized terrains, all runtime computations (elevation-map upsampling, terrain detail synthesis, normal-map computation, and rendering) are performed entirely within the graphics card, leaving the CPU basically idle. For compressed terrains, the CPU incrementally decompresses and uploads data to the graphics card (see Section 2.4).

Data Structures

To summarize, the main data structures are as follows. We predefine a small set of constant vertex and index buffers to encode the (x, y) geometry of the clipmap grids. And for each level 0 . . . L–1, we allocate an elevation map (a 1-channel floating-point 2D texture) and a normal map (a 4-channel 8-bit 2D texture). All these data structures reside in video memory.

Clipmap Size

Because the outer perimeter of each level must lie on the grid of the next-coarser level (as shown in Figure 2-4), the grid size n must be odd. Hardware may be optimized for texture sizes that are powers of 2, so we choose n = 2^k -1 (that is, 1 less than a power of 2) leaving 1 row and 1 column of the textures unused. Most of our examples use n = 255.

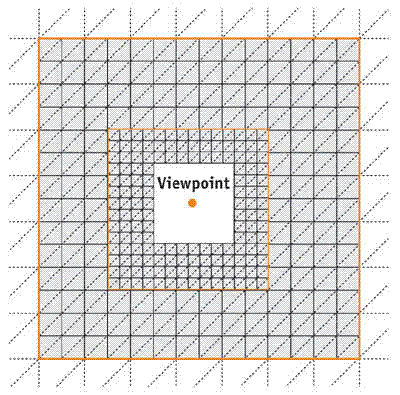
Figure 2-4 Two Successive Clipmap Rings

The choice of grid size n = 2^k -1 has the further advantage that the finer level is never exactly centered with respect to its parent next-coarser level. In other words, it is always offset by 1 grid unit either left or right, as well as either top or bottom (see Figure 2-4), depending on the position of the viewpoint. In fact, it is necessary to allow a finer level to shift while its next-coarser level stays fixed, and therefore the finer level must sometimes be off-center with respect to the next-coarser level. An alternative choice of grid size, such as n = 2^k -3, would provide the possibility for exact centering, but it would still require the handling of off-center cases and thus result in greater overall complexity.

Summary and Improvements

We have presented a GPU implementation of the geometry clipmap framework. The representation of geometry using regular grids allows nearly all computation to proceed on the graphics card, thereby offloading work from the CPU. The system supports interactive flight over a 20-billion-sample grid of the U.S. data set stored in just 355 MB of memory at around 90 frames/sec.

Vertex Textures

Geometry clipmaps use vertex textures in a very special, limited way: the texels are accessed essentially in raster-scan order, and in one-to-one correspondence with vertices. Thus, we can hope for future mechanisms that would allow increased rendering efficiency.

Eliminating Normal Maps

It should be possible to directly compute normals in the pixel shader by accessing four filtered samples of the elevation map. At present, vertex texture lookups require that the elevation maps be stored in 32-bit floating-point images, which do not support efficient bilinear filtering.

Memory-Free Terrain Synthesis

Fractal terrain synthesis is so fast on the GPU that we can consider regenerating the clipmap levels during every frame, thereby saving video memory. We allocate two textures, T 1 and T 2, and toggle between them as follows. Let T 1 initially contain the coarse geometry used to seed the synthesis process. First, we use T 1 as a source texture in the update pixel shader to upsample and synthesize the next-finer level into the destination texture T 2. Second, we use T 1 as a vertex texture to render its clipmap ring. Then, we swap the roles of the two textures and iterate the process until all levels are synthesized and rendered. Initial experiments are extremely promising, with frame rates of about 59 frames/sec using L = 9 levels.

References

Fournier, Alain, Don Fussell, and Loren Carpenter. 1982. "Computer Rendering of Stochastic Models." Communications of the ACM 25(6), June 1982, pp. 371–384.
Gerasimov, Philip, Randima Fernando, and Simon Green. 2004. "Shader Model 3.0: Using Vertex Textures." NVIDIA white paper DA-01373-001_v00, June 2004. Available online at http://developer.nvidia.com/object/using_vertex_textures.html.
Kobbelt, Leif. 1996. "Interpolatory Subdivision on Open Quadrilateral Nets with Arbitrary Topology." In Eurographics 1996, pp. 409–420.
Losasso, Frank, and Hugues Hoppe. 2004. "Geometry Clipmaps: Terrain Rendering Using Nested Regular Grids." ACM Transactions on Graphics (Proceedings of SIGGRAPH 2004) 23(3), pp. 769–776.
Malvar, Henrique. 2000. "Fast Progressive Image Coding without Wavelets." In Data Compression Conference (DCC '00), pp. 243–252.
Tanner, Christopher, Christopher Migdal, and Michael Jones. 1998. "The Clipmap: A Virtual Mipmap." In Computer Graphics (Proceedings of SIGGRAPH 98), pp. 151–158.