Визуализация массивов поверхностей с использованием

управляемых кластерных уровней детализации

Часть 2

Thatcher Ulrich
Oddworld Inhabitants
tu@tulrich.com

Перевод с английского: Лисеенко В.В.

Источник: http://tulrich.com/geekstuff/sig-notes.pdf

11 Первоклассное заполнение

Есть несколько способов исправить трещины между сетками. Один очевидный подход всегда уничтожать края кластеров по некоторой глобальной постоянной геометрической ошибке, независимо от фактической "S" в кластере. К сожалению, это серьезно ограничивает масштабируемость. Лучшие вариации к этому - ограничить отношения соседних кластеров, и всегда уничтожать к регулярному масштабу относительно изображения на крае [6] [9], хотя это и не является оптимальным.

Рисунок 2 - Использование флангов для заполнения трещин. Белый треугольник слева – это трещина между двумя сетками. Фланг (отмечены черным цветом) добавляется к одной из сеток, она распространяется на другие сети и проникает, охватывая трещины.

Другой метод заключается в добавлении фланга вокруг каждого кластера, итак сетки проникают по-немногу. Это должно хорошо работать, но избежать артефактов становится сложнее. В частности, выбор угла и размеров флангов является специальным и зависит от точной геометрии соседа. Правильное текстурирование флангов является сложным.

Еще одним подходом является объединение кластеров со специальными сетками. Они могут быть получены с использованием двух-или трех-уровневой схемы, путем присоединения края интерьера кластера с краем интерьера соседних кластеров. К сожалению, это может быть сложным, поскольку требует явного определения внутри каждого блока, и отношение между специальными сетками и экранно-пространственной ошибкой не ясно.

Рисунок 3 - Использование ленты для заполнения трещины. Вертикальная лента (отмечена черным цветом), которая прекрасно заполняет трещины, была добавлена, путем обмена вершин, смежных с трещиной.

Несколько проще вышеописанных вариаций для создания вертикальной ленты сетки, присоединить ребра между кластерами. Это работает только от края вершины кластера и визуально очень эффективно. Обратите внимание, что вертикальные ленты сетки пребывают в пределах блока, и могут быть затенены с использованием текстуры связанного кластера. Ясно, что это приводит к растяжению вертикальной текстуры над лентой, но отметим, что лента всегда меньше, чем "r" пикселей на экране. При разумных значениях “r", растяжения практически невозможно обнаружить. Этот метод еще довольно сложный, особенно в сочетании с решением анти-выталкивания, описанным ниже, потому что он в тесной зависимости от точной геометрии обоих краев кластеров.

Рисунок 4 - Использование стенки для заполнения трещины. Вертикальная стенка (отмечена черным цветом) была добавлена в один из кластеров, чтобы заполнить трещины, фактически не распространяется на другие кластеры.

Метод заполнения трещин, который я предпочитаю сочетает в себе достоинства флангов и лент. Идея просто создать вертикальную "стенку" по периметру каждой части. Верхняя часть стенки соответствует краю кластера, а дно ничему не соответствует. Требование нижнего края стенки в том, что он находится ниже полной сетки LOD на краю, а также ниже любого возможного упрощенного края. Кроме того, мы хотели бы, чтобы стенка была как можно короче для сохранения скорости заполнения. Как и фланги, стенки автономны от кластера и состоят из простых статических треугольников. Как и ленты, стенки не распространяются на интерьер любого соседнего узла и могут быть текстурированы, просто используя существующую текстуру кластера.

Рисунок 5 - Растяжение текстуры на вертикальных стенках (в выделенной области), "r" был установлен до 35, чтобы проиллюстрировать растяжение. Для более нормальных значений "r" (обычно <5), растяжение текстуры очень трудно увидеть.

12 Отход от выталкивания

Как уже упоминалось выше, мы можем скрыть некрасивые визуальные переходы, когда кластер распадается на дочерние кластеры, или когда дочерние кластеры сливаются в родительский блок. Решение включает в себя применение малого (возможно, 0) морфинга для вертикальной координаты каждой вершины в кластере сетки, с помощью одного параметра равномерного морфинга над целым кластером. Цель морфинга вычисляется следующим образом: для каждой вершины в кластере цели морфинга имеют те же горизонтальные координаты. Вертикальная координата вычисляется путем отбора примеров высот родительского кластера и известных горизонтальных координат.

Во время визуализации, мы будем вычислять морфинг параметров кластера, гарантируя, что параметр морфинга всегда равен 0, когда кластер собирается разделиться, и 1, когда кластер собирается объединиться. Это гарантирует то, что форма кластера на расстоянии, на котором происходит раскол совпадает с формой кусков кластера на бесконечно близком расстоянии после раскола кластера.

Рисунок 6 - 2D иллюстрация избегания выталкивания. Слева линия с двумя вершинами представляющая часть кластера с низкой детализации. В середине, она была заменена линией с тремя вершинами, представляющей дочерний кластер с большей детализацией. Пунктирная линия показывает желаемую истинную форму кластера, но средняя вершина была превращена в соответствии с родительским кластером с более низкой детализацией. На правом, средняя вершина перешла в желаемую позицию.

Перегруппировав нашу ошибку метрики, мы можем непосредственно вычислить такой параметр морфинга как расстояние до кластера.

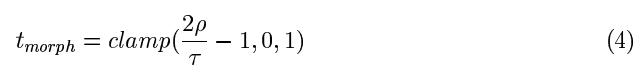
Эта формула дает t_morph = 0 в расстоянии, на котором родительский кусок расщепляется (потому что родительская "S" является двойной "S" ребенка, и ограничивающий родительский объем содержит ребенка). Она производит t_morph = 1 ровно в момент, когда кластер сам разделяется. Это линейно интерполирует t_morph между этими расстояниями, а зритель получает близко к кластеру.

Это позволяет избежать визуальных артефактов, вызванных одновременным выталкиванием многих вершин. В самом деле, это полностью исключает все вершины появляющиеся по всему дереву, заменяя их вместо этого тонким морфингом. Фактический LOD переход на обнаруживается зрителем, когда кластер делится на своих детей. Обратите внимание, что при использовании нашей простой ошибки метрики, морфинг полностью основан на расстоянии точки зрения, которая имеет хорошие свойства, потому что сетка морфируется, когда точки зрения движется. Это еще больше снижает заметность морфинга.

Стоимость данных этой схемы морфинга это добавление цели морфинга или дельта морфинга на вершину. Дельта морфинга может быть предпочтительна, поскольку она может быть квантованной в очень малое количество бит. Дельта морфинга всегда будет меньше, чем "r" пикселей на экране, так что ошибки квантования в пространстве экрана меньше, чем "r" / (2^N), где N - это количество бит, выделяемых для дельта морфинга.

Существует также обработка на лету данных необходимых для настройки вершин. Потому что параметр морфинга однороден по всему кластеру, и вершина данных кластера это линейный массив, который процессор реализует достаточно быстро, чтобы обеспечить загрузку GPU. Программа прямых вершин (вершинные шейдеры) может быть использована вместо этого, для снижения нагрузки на процессор.

13 Текстурирование

Текстурирование для этой LOD-схемы очень просто - в предварительной обработке, мы просто обеспечиваем статическую текстуру для каждого статического кластера. Учитывая знания экранно-пространственной ошибки метрики, используемой во время выполнения, и верхняя граница значения времени "r", наш препроцессор может гарантировать, что прогнозируемый размер тексель во время выполнения не будет превышать 1 тексель на пиксель. Математика выглядит следующим образом: Пусть Dmin будет минимальным геометрическим расстоянием, на котором блок будет отображаться. Из формулы 1, имеем:

где T_s является прогнозируемым размером текселя на экране, и T_g геометрический размер для текселя текстуры кластера. Решая T_g, и подставляя 1 для T_s, мы получаем:

Мы можем использовать эту формулу для T_g, чтобы усилить минимальное разрешение текстур для каждого блока во время предварительной обработки. Заметим, что если мы используем простое 2D-отображения связывания текстурных координат, эта формула не учитывает текстуру растяжения из-за круто наклоненных поверхностей. Мы можем дополнительно вычислить текстуры растяжения, на основе известной геометрии кластера, и принять его во внимание.

14 Сжатие

Кластерная иерархия, заполнения трещин сетки и информация вершин морфинга накладывают существенные накладные расходы на размер хранилища, необходимого для кластера дерева, по сравнению с простой статической сеткой одного и того же объекта или картой высот. Однако есть несколько существенных факторов, которые помогают компенсировать эти затраты.

Предварительный этап в кластерном LOD полностью отбрасывает вершины, которые не являются необходимыми для аппроксимации сетки с точностью до минимального значения "S" (на самом высоком уровне детализации в дереве). Это действует как вид сжатия с потерями на оригинальной карте высот. Плоские области в значительной степени уничтожены. Для типичных реальных DEM моделей, сжатие, как правило, значительно, даже по очень скромным деградациям в форме карты высот.

Другой потенциально полезное свойство кластерного LOD в том, что вершины в отдельных кластерах пространственно локализованы. Кластеры разных размеров в мировых координатах, но благодаря алгоритму LOD, остаются в пределах ограниченных координатами экрана. Если вершины в кластере сжимаются с помощью простой схемы квантования, ошибки квантования будут ограничены в пространстве экрана. Это не очень правильно, при масштабировании к кластеру с высшим уровнем детализации, однако, для разумной глубины дерева (например, до 8 уровней) 8 бит точности должно быть достаточно даже для больших наборов данных.

Принимая во внимание все накладные расходы, эталонную реализацию кластера препроцессор производит файлы данных кластера (геометрии только, не текстуры) в диапазоне от около 25 до 35 байт на единственный выход вершины, в зависимости от данных и предварительной обработки параметров. Для типичных данных DEM и очень скромного сжатия с потерями, это может соответствовать примерно от 5 до 7 байт на образец карты высот в исходных данных. Эти цифры еще не отражают агрессию квантования сжатия, возможности которых упомянуты выше, итак реалистичный минимальный размер данных для кластерного LOD будет меньше.

15 Загрузка кластеров

Все сетки и текстурные данные для каждого блока являются самодостаточными. Это делает его довольно простым к страничному выводу по требованию. Общий подход состоит в запуске отдельный потока, который отвечает за загрузку данных кластера. Визуализируемый псевдокод изменяется следующим образом:

Кроме того загружаемый поток должен свободного храниться, используя данные геометрии узла, когда он не используется в течение некоторого времени.

16 Реализация

Я сделал бесплатную, общую реализацию область алгоритма кластерного LOD, представленную здесь. Он работает на Windows и Linux, и должна быть адаптирована к другим платформам. Я призываю всех, кто заинтересован в использовании и адаптации кода для любых целей. Исправления ошибок и улучшения всегда приветствуются, конечно, и нет никаких ограничений в том, как код может быть использован.

17 Благодарности

Выражаем благодарность жителям Одворда за поддержку презентации этой работы и содействия рабочей среде, где рекомендуются личные исследования. Шон Барретт, Чарльз Блум, Джон Блоу, Марк Дучено, Том Форсайт, Джош Левенберга и Аарон Пфайффер за комментарии, критику и идеи. Тьерри Бергер-Перри и Майк Шева за обеспечение дополнительным кодом, исправлением ошибок, и построить улучшений Linux. Джон Ратклифф, Питер Линдстром, Бен Диское, Кен Масгрейв, Университет Вашингтона и Геологической службы США за предоставление образцов данных.

Литература

[1] C. Bloom. View independent progressive meshes VIPM). World wide web, Jun 000. http://www.cbloom.com/3d/techdocs/vipm.txt

[2] D. Cline and P. K. Egbert. Terrain decimation through quadtree morphing. IEEE Transactions o n Visualization and Computer Graphics, 7(l):62-69, Jan-Mar 2001

[3] W. H. de Boer. Fast terrain rendering using geometrical MIP mapping. World wide web, Oct 2000. http://www.flipcodecom/tutorials/tutgeomipmapsshtml

[4] M. A. Duchaineau, M. Wolinsky, D. E. Sigeti, M. C. Miller, C. Aldrich, and M. B. Mineev-Weinstein. ROAMing terrain: Realtime optimally adapting meshes. In IEEE Visualization '97, pages 8188, 1997.

[5] H. Hoppe. Progressive meshes. In Proceedings SIGGRAPH 96, pages 99108. ACM 1996.

[6] J. Levenberg. Fast view-dependent level-of-detail rendering using cached geometry. Forthcoming, Mar 2002.