Источник: http://hexlet.ru/blog/parallel/91.html
Авторы: Рахим ‘freetonik’

Ускорения параллельных вычислений

Главной целью создания и разроботки многочисленных типов параллельных машин, о которых мы говорили в прошлой статье, это скорость. Суперкомпьютеры и многопроцессорные системы могут и должны делать все быстрее! Давайте постараемся расчитать, насколько быстрее.

Логично подумать, что если один процессор выполняет работу на n секунд, то четыре процессора потратят n/4 секунд. Понятие “фактор ускорения” (“speedup factor”) это отношение времени, которое тратит на выполнение работы один процессор к времени, которое тратит на эту же работу многопроцессорная система.

S(p) = T_s / T_p

Для расчета важно использовать самый оптимальный T_s, то есть лучший из возможных не-параллельных алгоритмов.

Теперь плохие новости: у этого ускорения есть лимит. Называется он Amdahl’s Law (Закон Амдала) и вот его суть: так выглядит какая-либо задача на обычной однопроцессорной системе:


Все время выполнения — знакомое уже нам T_s, состоит из той части, которую можно распределить на несколько процессоров (распараллелить) — (1-f)T_s, и той части, что распараллелить нельзя (серийная) — fT_s.

Как будет выглядеть схема той же задачи для нескольких процессоров?



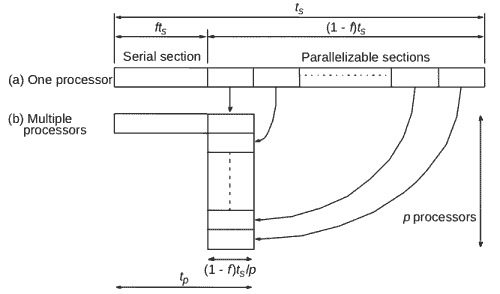
Теперь общее время выполнения Tp состоит из серийного времени и максимального из тех, что мы распределили на несколько процессоров (выполняются они все одновременно, но ждать нужно самого медленного). Для простоты допустим, что все они занимают одинаковое время.

Фактор ускорения расчитывается по формуле:



То есть все зависит от того, какой кусок программы мы сможем распараллелить (f в процентах означает количество серийного кода). Если f=0%, то есть абсолютно весь код распараллелен (чего практически не может быть), то чем больше процессоров мы задействуем, тем быстрее будет выполнена задача, и соотношение будет линейное: хотим в 10 раз быстрее — используем десять процессоров, хотим в миллион раз быстрее — закупаем миллион процессоров. Но вот стоит оставить 5% серийного кода, а 95% распараллелить, то фактор ускорения будет равен 20 и выше никак не прыгнуть. Даже если закупим к тому миллиону еще миллион процессоров, то программа все равно будет выполняться в 20 раз быстрее. Вот как этот грустный факт выглядит на графике с примерами разных процентов f:



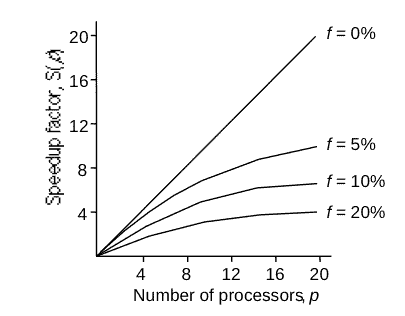
Получается, что самое важное в вопросе эффективности параллельного кода — это хороший дизайн самого алгоритма. Каждая деталь может сильно повлиять на расширяемость: если сейчас алгоритм нормально использует ресурсы четырехядерного процессора, то возможно больше 8 ядер он нормально использовать не сможет, и тогда через год программу нужно будет писать заново — ведь вместо количества транзисторов теперь каждые полгода увеличивается количество ядер!

Чтобы написать хороший параллельный алгоритм, нужно вникнуть в суть проблемы и подумать, как его можно разделить на отдельные независимые (в идеале) части, чтобы все они выполнялись параллельно на разных процессорах. Посмотрим на примере довольно ёмкой задачи умножения матрицы А на вектор b. Результат будет записан в вектор y, который по размеру идентичен вектору b. Чтобы получить первое значение вектора y, нужно умножить первую строку матрицы на вектор b, чтобы получить второе значение y — вторую строку на b, и так далее. Получается, каждый элемент вектора y можно считать независимо от других, то есть параллельно.



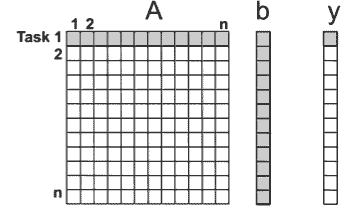
Размер каждой такой задачи один и тот же — все строки A имеют одинаковый размер (пока не касаемся таких деталей, как плотность матрицы — возможно, в ней много нулей, но предположим, что это не сильно влияет на время выполнения). Нет никаких зависимостей между задачами, и все задачи используют один и тот же b.

Вот другой пример — запрос в базу данных:

MODEL = “CIVIC” AND YEAR=2001 AND (COLOR=”GREEN” OR COLOR=”WHITE”);

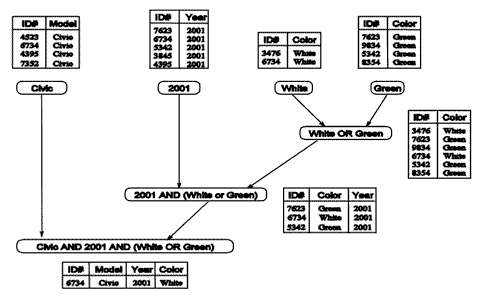
Запрос пытается получить все зеленые или белые Цивики 2001 года из такой базы:



Такую задачу можно разложить на три части: один процессор будет формировать таблицу все Цивиков 2001 года, другой процессор будет формировать таблицу всех белых и зеленых машин (эти два запроса могут идти параллельно), после чего результат join’а этих двух таблиц и будет ответом.



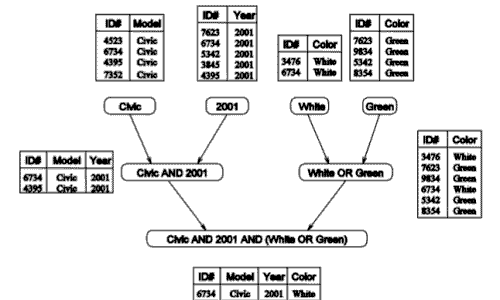
Можно изменить структуру запроса, что может повлиять на параллелизацию



Разделение задачи на части для последующего распределения этих частей на разные процессоры называется декомпозицией. Умножение матрицы на вектор это пример декомпозиции результата задачи: результат (вектор y) был разделен на несколько независимых частей и каждая расчитывалась отдельно от другой. То же самое можно сделать и с перемножением матриц: