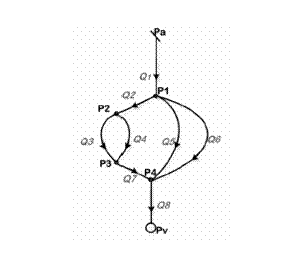
Рисунок 1 - Граф тестового мережного об'єкту
MIMD-паралельний вирішувач рівнянь для мережного
динамічного об’єкту з розподіленими параметрами
Гусєва Г.Б., Молдованова О.В.
Кафедра ЕОМ ДонНТУ
anna-guseva@ukr.net
Gusyeva G.B., Moldovanova O.V. MIMD parallel equation solver for dynamic distributed parameter network objects: The article describes using of one-step two-point block numerical method for simulation of complex dynamic distributed parameters network objects (DDPNO). The approaches to parallelization of equation solver for the DNO simulation are examined in this article. Virtual parallel model of equation solver is developed and necessary steps of its devirtualization are emphasized. The target computing MIMD resource is also briefly represented. The results of experimental researches are also given in this article.
Розвиток чисельних методів для вирішення систем нелінійних диференціальних рівнянь привів до появи широкого спектру програмних пакетів для чисельного аналізу i динамічного моделювання в багатьох галузях, таких як хімічна, біологічна, гірнича справа та інші. При збільшенні розмірності моделюючої системи, кількості її параметрів, що характеризують динамічні процеси, з’являється необхідність в аналізі підходів до розпаралелювання обчислень. Метою розпаралелювання є досягнення ефективного та швидкого вирішення на багатопроцесорних високопродуктивних обчислювальних системах таких складних науково- технічних задач, які неможливо вирішити на машинах фон- неймановського типу. Але на теперішній час існує не так багато чисельних методів інтегрування диференціальних рівнянь, орієнтованих на обчислювальну систему з паралельною архітектурою. Більшість з них мають складну структуру, що приводить до втрати ефективності. Тому питання дослідження нових паралельних чисельних методів, позбавлених вказаних недоліків, є безсумнівно актуальним.
Мережні динамічні об'єкти (МДО) відносяться до класу технічно- складних систем, таких як газо- та водопостачання, шахтні вентиляційні мережі, електричні мережі та ін. Структура складних динамічних систем характеризується нелінійністю характеристик, великою розмірністю та розподіленістю параметрів процесів, тому майже не піддається аналітичному аналізу. Основним методом вирішення задач автоматизації та технологічного проектування є математичне моделювання. Формальний опис МДО складається з двох суттєвих частин [1, 2]: опису топології та опису рівнянь фізичних процесів, що мають місце в гілках та вузлах мережі. З точки зору математичного опису динаміки процесів мережний об'єкт можна поділити на два класи: МДО з зосередженими параметрами (МДОЗП) і МДО з розподіленими параметрами (МДОРП). Для описання МДОРП використовуються еліптичні, параболічні, гіперболічні та спеціальні диференціальні рівняння у часткових похідних.
Для останньої системи рівнянь змінна стану в кожний момент часу – це функція відносно однієї або декількох координат простору. Об'єктом дослідження є шахтна вентиляційна мережа (ШВМ) (рис. 1). Топологія ШВМ представляється у вигляді графа.
Рисунок 1 - Граф тестового мережного об'єкту
Для гілки з індексом і процеси зміни значення потоку повітря Qi та тиску Pi представляються у вигляді наступних рівнянь [1]:
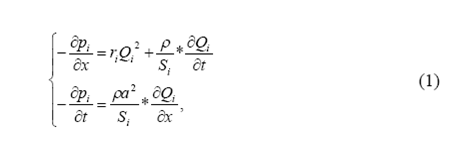
де ri– питомий аеродинамічний опір; а – швидкість звуку в повітрі (330 м/сек.); 
– густина повітря; Si– площа перетину гілки; х – координата вздовж гілки. Наступним кроком є приведення системи рівнянь до вигляду, придатного для чисельного вирішення. Цей крок включає апроксимацію диференціальних рівнянь у часткових похідних за методом прямих та їх розрішення відносно похідних тих змінних, що мають бути визначені [5].
Розглянемо розбивку j-ої гілки ШВМ за методом прямих (рис. 2).
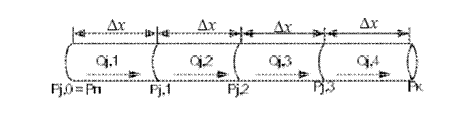
Рисунок 2 - Апроксимація j-ої гілки ШВМ за методом прямих
Тут гілку було розбито на М елементів із постійним кроком дискретизації 
. Граничні умови: Рп = Ратм, Рк= f(Q), де Ратм – атмосферний тиск.
Система рівнянь буде виглядати наступним чином:
де q = 1, 2, … М. Надалі необхідно обрати чисельний метод для розв’язання отриманої після апроксимації системи диференціальних рівнянь.
Блоковим будемо називати метод, при якому для блоку з k точок нові k значень функції обчислюються одночасно. Ця особливість методів, по- перше, узгоджується з архітектурою паралельних обчислювальних систем, а, по-друге, дозволяє обчислювати коефіцієнти різницевих формул не в процесі інтегрування, а на етапі розробки методу, що значно збільшує ефективність обчислень.
Паралельні блокові чисельні методи розв'язують задачу Коші. Для звичайного диференціального рівняння першого порядку задача Коші має наступний вигляд [3, 4]:
Розглянемо рішення задачі Коші k точковим блоковим методом (рис. 3). Множину М точок рівномірної сітки {tm}, m = 1,2,…,M з кроком 
розіб'ємо на блоки, що містять по k точок , 
. У кожному блоці уведемо номер точки i = 0,1,…, k та позначимо через tn,i точку n – го блоку з номером і. Точку tn,0 назвемо початком блоку n, а tn,k – кінцем блоку. Очевидно, що tn,k = tn + tn,0 . При цьому початкова точка до блоку не включається.
Рисунок 3 - Схема розбиття на блоки
Існує два типи блокових методів: однокроковi та багатокроковi блокові методи. Якщо для розрахунку значень у новому блоці використовується тільки остання точка попереднього блоку – мова ведеться про однокроковий блоковий метод (рис. 4).
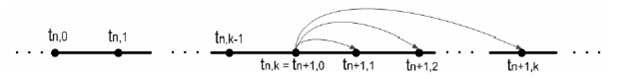
Рисунок 4 - Схема обчислення однокроковим блоковим методом
У загальному випадку рівняння m-крокового k-точкового блокового методу записується у наступному вигляді [3, 4]:
Де:
Надалі будемо досліджувати однокроковий блоковий метод. На рис. 5 представлено шаблон однокрокової k-точкової різницевої схеми.
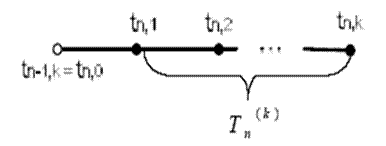
Рисунок 5 - Шаблон однокрокової k-точкової різницевої схеми
Формула для обчислення нових k значень є наступною:
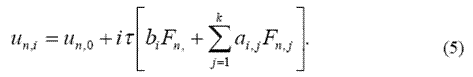
Для визначення коефіцієнтів ai,j та bi треба побудувати інтерполяційний багаточлен Лагранжа Lk(t) із вузлами інтерполяції tn, i,i=0,1,…,k та відповідними до них значеннями Fn,
i = f(tn ,i, un, i) і проінтегрувати у границях (tn, tn+i
). Формули для двоточкового блокового методу при k = 2 будуть мати наступний вигляд:
Оскільки для обчислення наближених значень рішення задачі Коши необхідно вирішити нелінійну систему рівнянь, можна використовувати для цього наступний ітераційний процес:
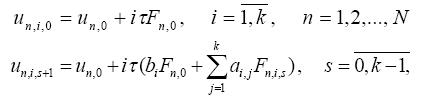
де n – номер блоку, і – номер точки блоку, s – номер ітерації. Метод ітерацій дозволяє проводити обчислення паралельно для кожного вузла блоку. Після виконання k кроків обчислювань локальна помилка у вузлах блоку буде мати порядок О( 
). Таким чином, двоточковий метод має порядок апроксимації О(
) [3, 4].
На основі блокового однокрокового двоточкового методу було розроблено послідовний вирішувач рівнянь для тестової ШВМ [6]. Для встановлення працездатності послідовної імплементації вирішувача рівнянь було проведено чотири групи експериментів (табл. 1).
Результати експериментів підтвердили працездатність послідовного вирішувача рівнянь, заснованого на блоковому однокроковому двоточковому чисельному методі, і можливість його використання для моделювання складних МДО.
Експериментально було визначено, що блоковий метод відзначається кращою збіжністю та точністю обчислень, ніж метод Адамса-Башфорта другого порядку точності.
Таблиця 1. Опис проведених експериментів
Одним із необхідних етапів при розробці паралельного программного забезпечення для моделювання МДОРП є створення паралельної віртуальної моделі об'єкту, що буде являти собою набір взаємопов’язаних паралельно працюючих процесів, кожний з яких займається обчисленням визначеної частини графу дискретизованого мережного об'єкту [5].
Обсяг даних, якими обмінюються віртуальні паралельні процеси, і кількість самих процесів, потрібних для рішення задачі моделювання МДОРП, залежать не тільки від розмірності та складності топології мережного об'єкту, але й від особливостей архітектури наявного паралельного обчислювального ресурсу та способу угруповання й розподілу віртуальних процесів. Процес переходу від віртуальної паралельної MIMD-ЕОМ до цільової, особливостям якої повинна відповідати структура програмного забезпечення, що розроблюється, називається процесом девіртуалізації [5].
Проведені експериментальні дослідження доказали, що блоковий однокроковий двоточковий метод може використовуватися для рішення задач моделювання МДОРП. Крім того, у порівнянні з досить розповсюдженим методом Адамса-Башфорта другого порядку він показує кращі результати у тривалості рішення та має вищу точність обчислень.
Експериментально було визначено, що при розробці паралельної віртуальної моделі вирішувача рівнянь для складних МДО не має сенсу розбивати задачу на такі невеликі обчислювальні ділянки, яких потребують перші два рівні розпаралелювання. Час роботи паралельної задачі збільшується за рахунок великої кількості обмінів між процесорами, при тому що реальний обсяг обчислень на кожний процесор є незначним. Тому була поставлена задача об'єднання або «укрупнення» віртуальних процесів з метою зниження кількості комунікаційних ліній. При розбивці графа МДО, тобто на четвертому рівні, було отримано найвищу ефективність від розпаралелювання.
Крім того, слід відмітити, що при використанні блокувальних двонаправлених та неблокувальних однонаправлених МРІ-функцій, що здійснюють комунікацію між МРІ-процесами, досягається більша ефективність від розпаралелювання задачі моделювання МДО. Таку комбінацію функцій рекомендується використовувати тільки у тих випадках, коли треба здійснити невелику кількість операцій обміну. Хоча двонаправлена функція має вищу швидкість передачі даних, але час виконання паралельної задачі може збільшитися за рахунок очікування завершення обмінів кожної з цих блокувальних функцій.
1. Абрамов Ф.А., Фельдман Л.П., Святный В.А. Моделирование динамических процессов рудничной аэрологии.– К.:Наук.думка, 1981.–284с.
2. Святный В.А. Моделирование аэрогазодинамических процессов и разработка систем управления проветриванием систем шахт. Докт. дисс., Донецьк, ДПИ, 1986.
3. Фельдман Л.П., Петренко А.І., Дмитрієва О.А. Чисельні методи в інформатиці. – К.: Видавнича група ВНV, 2006. – 480с.
4. Дмитриева О.А. Алгоритмические методы повышения эффективности параллельных вычислительных систем при решении многомерных динамических задач: Дис. канд. тех. наук: 05.13.13. – Донецк, 2001.
5. Svjatnyj V., Moldovanova O., Smagin A., Resch M., Keller R.: Rabenseifner. Virtuelle Simulationsmodelle und ein Devirtualisierungsvorgang für die Entwicklung der parallelen Simulatoren von komplexen dynamischen Systemen/ 19. Symposium ASIM 2006, Tagungsband, 2006, S. 416 – 421.
6. Гусєва Г.Б. Магістерська дисертація, ДонНТУ, Донецьк, 2007.
Дата надходження до редакції 03.12.2007 р.