The ProMoT/Diana Simulation Environment
K. Bondareva, O. Milokhov, K. Teplinskiy
National Technical University of Donetsk, Computer Science Faculty
M. Krasnyk, M. Ginkel, A Kienle
Max Planck Institute for Dynamics of Complex Technical Systems
Otto-von-Guericke-University Magdeburg
Source of information : The Vernadsky National Library of Ukraine. Scientific works of Donetsk National Technical University. Series: Problems of modeling and design automation
Abstract
M. Krasnyk, K. Bondareva, O. Milokhov, K. Teplinskiy, M. Ginkel, A. Kienle, The ProMoT/Diana Simulation Environment. This article introduces the object-oriented modeling tool ProMoT and the simulation environment Diana suitable for numerical analysis of problems in chemical engineering and systems biology. The key aspects of this environment are flexible structured models, an efficient modular numerical kernel, and the use of the scripting language Python as a powerful command line interface. The implementation is based on CAPE-OPEN interfaces to allow a modular software design and easy extensions of the system. The contribution discusses the design and implementation rationale of the simulation environment.
Motivation
With the increasing capabilities of modern computers, it appears possible in academia and industry to describe and analyze more complex problems with higher resolutions. To make this possible a good and ”easy to use” modeling tool is required, that allows to create sophisticated models and analyze them with robust and efficient simulation code. Usually engineers have the choice between well known commercial simulation environments, like VisSim, Simulink, DyMoLa, gPROMS, etc. These software packages are well established with considerable libraries in different engineering fields and have own communities. There are also efforts to develop standards for the exchange of models like Modelica or the Systems Biology Markup Language. We want to contribute our modeling and simulation environment ProMoT/Diana (the names stand for ”Process Modeling Tool” and ”Dynamic sImulation And Nonlinear Analysis” tool).
The special characteristics of ProMoT and Diana are, that they build on open source, freely available numerical code, provide sophisticated modeling and simulation capabilities for large models found in process engineering and systems biology, allow to be connected with other tools by common interfaces, allow to be easily extended for new requirements arising in academic research and will be freely available for academic groups. The following sections will discuss the general design of ProMoT and some aspects of the software design of Diana along with a short application example.
Modeling with ProMoT
Model setup
ProMoT is a general modeling tool for the object-oriented development of dynamic equation-based models. Its main fields of application are process engineering and systems biology. ProMoT does not contain a simulation system itself but it has been originally developed as modeling front-end for the simulation environment DIVA [1]. The model description used inside the tool is generic and in essence boils down to a tree of objects containing a symbolic system of ordinary differential and algebraic equations which describe continuous behavior. The models can also contain descriptions of discrete behavior that interact with the continuous equation set. The discrete part is described using the formalism of a deterministic, boolean valued Petri net. This formalism has been chosen for several reasons: i) places and transitions can be easily connected to the continuous model as boolean variables or discrete events respectively; ii) Petri networks are easy to modularize, allowing for encapsulated descriptions of local discrete processes; iii) local discrete parts can act asynchronously but can also be connected to describe the synchronization of events.
These characteristics render Petri networks as a good tool to describe discrete model changes based on physical phenomena as well as programmed controllers for process engineering models [2].
The model description inside ProMoT is quite general and is not limited to work with one specific simulation framework. Therefore the models can be exported for different simulation environments like Matlab, Diva and last but not least for our new simulation environment Diana.
Models in ProMoT can be setup using the modeling language MDL or by aggregation and connection of existing modules in a graphical editor. For more information about this topic see [3, 4]. The structuring follows the multi-level framework of network-theory, which is more extensively described in [2,5]. Based on this framework, several modeling libraries have been implemented for different application fields like e.g. reaction and separation systems with vapour-liquid equilibrium [4], membrane reactors, fuel cells and models in systems biology [3].
When the user has finished the work on the model, the modeling tool allows performing different static tests of the dependency structure of the equation set to detect modeling errors and helps to debug the model. Furthermore the equation structure allows optimizing the equation set for efficient simulation; this is further elaborated in [2]. The derived equation structure is also exported to most of the simulation environments as equation pattern to allow efficient calculations using numeric algorithms and sparse matrix techniques.
Code generation design
Code generation starts with an instantiated and optimized model. Since there are different output formats with own characteristics, the code generation is not implemented in methods of the model but in separate classes that interact with the model in a protocol similar to the strategy design pattern [6]. In this way it becomes easier to maintain multiple output formats without continuously changing all model classes.
In the case of code-generation for Diana, the original structure of the model is not exported, because the simulator only supports equation sets with fixed structure and structured computation would be less efficient for large scale models.
The generated code implements a subclass of the generic abstract model class of Diana. The generic class realizes most functionalities and interfaces for memory allocation, variable access, computation of approximate Jacobian matrices by finite differences and generic methods to evaluate the state and transitions of the Petri network.
The specific model class must realize the specific initialization of the model, the calculation of intermediate variables and residuals. It can also implement some optional functions. If the model has a discrete part it will implement a specifically structured Petri network and the respective trigger functions. If there are a specific requirements on accuracy, e.g. if sensitivity analysis or continuations are desired, the model can implement methods for analytic calculation of Jacobians.
Analytic Jacobians are derived using the symbolic differentiation algorithm implemented in the computer algebra system Maxima. We have implemented some special functions to generate optimized code for Jacobian matrices calculation of iterative equations and for derivatives of higher order.
Numerical analysis with Diana
General design rationale
The generic interfaces for solvers and models in Diana are based on the specifications developed by the CAPE-OPEN community [7]. These interfaces are designed to be used across an inter-process communication interface and they allow exchanging specific models and numeric algorithms without difficult changes of the sources. We use these interfaces wrapped into the Python scripting language as a command line user interface.
The creation of model and solver instances is in general performed in a factory design pattern, where the class for the object is identified by name. This abstraction is useful, because it will allow to get the instances in different ways: i) as a direct python instance ii) as an instance created from a dynamically loaded C++ shared library or iii) as an remote instance published by an external CAPE enabled simulation package. Currently we work with shared libraries.
Dynamic simulation
Dynamic simulation in the Diana environment is performed by a set of numerical differential algebraic solvers. All solvers implement the ICapeNumericDAESolver interface. This allows to use the solver instance as a ”black-box” integrator in Python scripts. The setup of the solver can be changed by a set of parameters: e.g. the relative error tolerance, the type of the internal linear algebra solver, etc. This parameter concept is derived from CAPE-OPEN; parameters have a name and a value, contain also a specification with default value and a documentation text, which makes them self-explanatory. In the same manner adjustments to models take place.
Solvers accept different reporting interfaces to process results of simulation directly. This allows to generate simulation logs or plots of simulation results. In Diana different integration codes have been used, like BDF or Runge-Kutta, this allows to solve different problem types, like systems of stiff ordinary or differential algebraic equations.
Parameter continuation
A continuation superclass has been developed for the Diana nonlinear analysis suite that allows to perform a numerical continuation of the solution for a specified subtask. The superclass realizes a predictor-corrector method with tangent or chord predictor and local or pseudo-arclength parameterization of the corrector. A Newton method with line search algorithm has been used as the corrector method. Continuation subclasses define the specific problem description by specifying residual vector and Jacobi matrix. Parameter continuation is used for the calculation of steady state solution branches and critical boundaries in the parameter space. During continuation the user has the possibility to determine the stability of the steady state. Stability analysis is applied to linearized model near steady state and based on the generalized eigenvalue problem. Such kind of analysis allows to detect events where real eigenvalue or pairs of the complex conjugate eigenvalues cross the imaginary axis.
Two additional continuation subclasses are used to find solution curves with conditions specified by an augmented system. The first augmented system is used for tracking Hopf points with pure imaginary eigenvalues. The second one is used for singularities with zero real eigenvalue. If the model has been generated with support for the calculation of higher order derivatives, it is possible to add supplementary conditional equations to find more complex singularities of the steady state continuation curve. Conditions for limit points, isola points, pitchfork bifurcation points, and winged cusp points have been implemented. More information about methods and applications of the singularity analysis can be found in [8].
Optimization
Numerical optimization is used to solve a variety of problems in process engineering and systems biology. There are currently running projects in our working team that involve model identification and system reengineering, experimental design and optimal control of engineering processes. These problems or optimization tasks mostly use some model of a physical or chemical process, but involve additional specific calculations of objective functions and constraints that cannot be carried out directly within the simulation of the model. Our main goal is to provide a kind of glue software with common interfaces that allows integrating different problem specifications with the different algorithms. The user should be required to program as little as possible, but must be able to customize the calculations for his specific optimization task.
In order to integrate algorithms which can solve different optimization tasks we propose a software architecture, where the optimization task is abstracted to a common interface separate from the algorithm. This interface allows to access optimization variables, to compute the objective function and optional inequality and equality constraints. Optionally also sensitivity matrices can be calculated by the task, but this is only required, if gradient based algorithms should be applied. Different algorithms can be applied to this abstracted interface, and the implementation effort integrate a new algorithm is reduced to a minimum since all model and problem specific calculations are in the responsibility of the optimization task.
There are different preimplemented concrete optimization tasks, which implement the abovementioned interface. On the one hand there are fully preimplemented tasks, e.g., parameter fitting, where simulated time courses of a model are adjusted to measurements from different experiments. In this case the user only configures the optimization task by supplying the model, the measured values and specific parameter sets. On the other hand there is the possibility to implement completely custom objective functions and constraints for an optimization with Python functions. In this way the optimization is highly flexible and the user is able to adjust the calculations very easily. Currently there are a deterministic multiple shooting algorithm and a genetic algorithm implemented [9].
Application example
The application is considered the dynamic simulation of a counter-current fixed-bed reactor with self-sustained oscillations. The model is represented by a system of discretized parabolic partial differential and algebraic equations. For details with a full model description and discussions of the results see [10].
The ProMoT compiler mdl2diana generates C++ source files for the model and uses an external compiler to produce a shared library with the model code. The following Python script realizes a simple dynamic simulation of the reactor model:
The ProMoT/Diana Simulation Environment
import diana, sys
main=diana.GetDianaMain(sys.argv);
mmanger=main.GetModelManager();
model=mmanger.CreateModel(diana.CAPE_CONTINUOUS, "GzfbrIdwt.so");
model.Initialize();
eso=model.GetActiveESO();
epar=eso.GetParameters(); evar=eso.GetStateVariables();
ri=main.CreateReportingInterface("basic");
ri.SetComponentName("data");
print "increase inlet temperatures of both tubes";
epar["t1_ein"].SetValue(600.0); epar["t2_ein"].SetValue(600.0);
print "adjust inlet concentrations";
epar["xa1_ein"].SetValue(0.003); epar["xa2_ein"].SetValue(0.003);
# create solver
sfactory=main.GetSolverFactory();
solver=sfactory.CreateSolver(diana.CAPE_DAE, model, "ida.so");
solver.Initialize();
solpar=solver.GetParameters();
solver.SetReportingInterface(ri);
ri.Add(solpar["T"]);
for i in xrange(epar["n_z"].GetValue()):
ri.Add(evar.ItemByName("t1[%d]"%(i+1)));
solpar["Tout"].SetValue(100); solpar["Tend"].SetValue(1000)
solver.Solve();
print "reduce inlet temperature in order to get oscillations"
epar["t1_ein"].SetValue(300.0); epar["t2_ein"].SetValue(300.0);
solpar["Tend"].SetValue(6000);
solver.Solve();
ri.WriteData("oscil.dat");
The evolution of the temperature profile in the reactor is shown in figure 1.
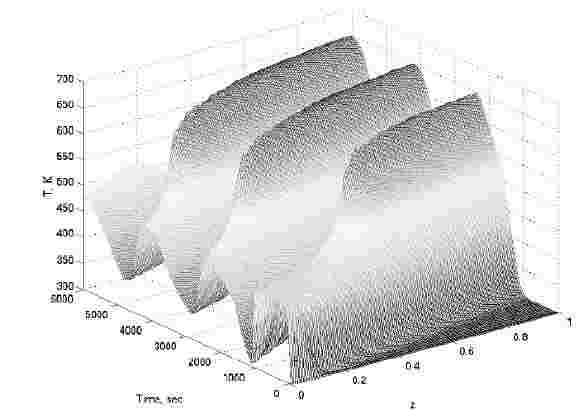
Figure 1. Results of dynamic simulation of the counter-current fixed bed reactor
Conclusion and future plans
ProMoT/Diana is an open-source and extensible modeling and simulation environment for process engineering and systems biology. It allows for object-oriented modeling, model exchange and provides an extensible architecture for numeric model analysis. By the use of Python it allows flexible extensions for users that are not experienced programmers. In the future it is planned to extend the set of available numerical algorithms. Also a network layer will be developed based on CAPE-OPEN that allows to connect Diana with other simulation packages via a CORBA middleware.
References
- 1. K. D. Mohl, A. Spieker, R. Köhler, E. D. Gilles, and M. Zeitz. DIVA - A simulation environment for chemical engineering applications. In ICCS Collect. Vol. Sci. Pap., pp. 8–15. Donetsk State Techn. University, Ukraine, 1997.
- 2. M. Mangold, O. Angeles-Palacios, M. Ginkel, R. Waschler, A. Kienle, and E.D. Gilles. Computer aided modeling of chemical and biological systems - methods, tools, and applications. Industrial & Engineering Chemistry Research, 44(8):2579–2591, 2005.
- 3. M. Ginkel, A. Kremling, T. Nutsch, R. Rehner, and E.D. Gilles. Modular modeling of cellular systems with ProMoT/DIVA. Bioinformatics, 19:1169–1176, 2003
- 4. R. Waschler, O. Angeles-Palacios, M. Ginkel, and A. Kienle. Object-oriented modeling of largescale chemical engineering processes with ProMoT. Mathematical and Computer Modeling of Dynamical Systems, 2005.
- 5. E.D. Gilles. Network theory for chemical processes. Chem. Engng. Technology, 21:121–132, 1998.
- 6. E. Gamma, R. Helm, R. Johnson, and John Vlissides. Design Patterns: Elements Reusable Object-Oriented Software. Addison Wesley, 1995.
- 7. M. Jarke, J. Koeller, W. Marquardt, L. von Wedel, and B. Braunschweig. CAPE-OPEN: Experiences from a standardization effort in chemical industries. Technical report, Lehrstuhl frü Prozesstechnik, RWTH Aachen, 1999.
- 8. M. Krasnyk, M. Ginkel, M. Mangold, and A. Kienle. Numerical analysis of higherorder singularities in complex process models in ProMoT. In PLu.igjaner and A. Espuña, editors, European Symposium on Computer Aided Process Enginienegr - ESCAPE-15, pp. 223–228. Elsevier, 2005.
- 9. K. Teplinskiy, V. Trubarov, and V. Svjatnyj. Optimization problems in the technological-oriented parallel simulation environment. pp. 582–587, Erlangen, 2005. SCS Publishing.
- 10. M. Mangold, F. Klose, E.D. Gilles. Dynamic behavior of a counter-current fixedbed reactor with sustained oscillations. In S. Pierucci, editor, European Symposium on Computer Aided Process Engineering - ESCAPE-10, pp. 205–210. Elsevier, 2000.
Дата надходження до редакції 03.10.2007 р.
