Значительная часть первых двух глав этой книги имела дело с поведением дискретных динамических систем, в частности семьи квадратных картографий. Наблюдались три основных типа поведения: фиксированный, периодический, и хаотический (или эргодический). Первые два вида поведения присутствуют во многих непрерывных динамических системах вида, описанного отличительными уравнениями с точными решениями. В этой главе сравнение будет сделано между самой известной непрерывной периодической системой, гармоническим осциллятором, и самой известной дискретной периодической системой, логистическим уравнением. Учитывая аналогичную природу этих двух систем, должна быть возможность выполнить параллельный анализ простого гармонического генератора и логистического уравнения. От такого исследования новая тема в дискретном динамическом анализе возникнет, а именно, аналог к ведомому гармоническому генератору: что я называю ведомым логистическим уравнением. В процессе, устройство для того, чтобы определить количество поведения повторенных картографий будет введено, образец Ляпунова, с косвенным результатом производства когда-либо более захватывающих изображений.
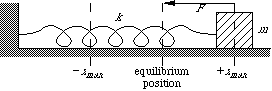
Простой гармонический осциллятор (ПГО) является массой, связанной с некоторым упругим объектом незначительной массы, которая установлена в другом конце и ограничена так, чтобы оно могло переместиться в только одном измерение. Эта упрощенная модель приближает много систем, которые вибрируют или колеблются: кожа барабана, струны гитары, квант механические описания атома, и т.д. Важность этой проблемы, однако, заключается в том, что уравнения подобной формы возникают, когда частица перемещается через любую область, у потенциала которой есть один или более местных минимумов: планетарное и спутниковое движение, классическое описание электрона в орбите вокруг ядра, маятников, и т.д. Подобные уравнения также возникают в исследовании цепочек LCR: тип, используемый в аналоговых коммуникационных устройствах и передаче электроэнергии. (Символы L, C, и R используются для обозначения электрических компонентов индуктивности, емкости, и сопротивления соответственно.)
Когда рассеивающие силы, такие как трение и сопротивление воздуха будут проигнорированы, чистая сила будет непосредственно пропорциональна смещению массы от положения равновесия системы и указывающий в противоположном направлении; условие, известное как закон Хука. Начиная со второго закона Ньютона, мы можем получить второе линейное дифференциальное уравнение, решение которого дает нам смещение массы как функция времени.
| Простой Гармонический Осциллятор |
| |
 |
| |
|
| Fnet = |
ma |
x |
= смещение |
| −kx = |
mẍ |
k |
= константа пружины |
| mẍ + kx = |
0 |
m |
= масса |
| x = |
A cos(ω0t + φ) |
A |
= амплитуда |
| ω0 = √ |
k |
|
 |
| m |
|
φ |
= фаза |
| ω0 |
= естественная частота |
Движение периодическое с частотой, которая зависит от природы массы и упругости объекта (здесь предполагается пружина). Амплитуда "A" и фаза "φ" [фи] является константами, определенными начальным смещением и скоростью системы.
Более реалистическая физическая модель - та, которая включает рассеивающие силы: заглушенный гармонический осциллятор. Ради простоты предположим, что любая рассеивающая сила непосредственно пропорциональна скорости массы и в противоположном направлении. Это - хорошее приближение поведения сопротивления воздуха и производит другое отличительное уравнение с точным решением. Фактически, это - единственный тип рассеивающей силы, для которой у отличительного уравнения движения есть точное решение.
| Затухающий Гармонический Осциллятор |
| |
|
| Fnet = |
ma |
b |
= коэффициент трения |
| −bẋ − kx = |
mẍ |
γ |
= фактор затухания |
| mẍ + bẋ + kx = |
0 |
ω1 |
= частота затухания |
| x = |
A e−γt cos(ω1t + φ) |
|
|
| |
ω0 = √ |
k |
|
γ = |
b |
|
ω1 = √(ω02 − γ2) |
 |
 |
| m |
2m |
|
У нас теперь есть уравнение, которое приводит к различному поведению для различных значений параметра. Когда фактор задержки равняется нолю, система уменьшает до случая простого гармонического осциллятора: длительное колебание в естественной частоте с постоянной амплитудой. Когда фактор затухания больше чем ноль, система может и не колеблется, в зависимости от отношения между фактором затухания "γ" [гамма] и естественной частотой ω0 [омега ноль].
| ω0 > γ |
Система находится под затуханием и показывает переходное поведение, колеблющееся в затухающей частоте с амплитудой, которая распадается по экспоненте. Если мы будем достаточно долго ждать, то система остановится в ее положение равновесия. |
| ω0 = γ |
Критически затухший случай. Система возвратится быстро и гладко к ее положению равновесия. Нет никакого колебательного поведения во все это время. Движение описано полностью показательным распадом. |
| ω0 < γ |
Выше затухшего случая. Решение - теперь сумма двух показательных условий распада, один медленнее, чем другой, и имеет форму |
| |
x = A1exp(−γ1t) + A2exp(−γ2t) где γ1 = γ + √(γ2 − ω02) и γ2 = γ − √(γ2 − ω02) |
| |
Движение приближается к устойчивому состоянию, но более медленно, чем в критически затухающем случае. |
Другая общая механическая неисправность возникает, когда заглушенный гармонический осциллятор ведет некоторая внешняя приложенная сила с временной зависимостью: ведомый гармонический осциллятор. Самый важный случай - случай силы, которая колеблется в синусоидальной манере. Если движущая сила имеет форму
F(t) = F0cos(ωt + φ0)
тогда у дифференциального уравнения есть точное решение.
| Ведомый Гармонический Осциллятор |
| |
|
| Fnet = |
ma |
F0 |
= максимальная движущая сила |
| F(t) − bẋ − kx = |
mẍ |
φ0 |
= движущая фаза |
| mẍ + bẋ + kx = |
F0cos(ωt + φ0) |
ω |
= движущая частота |
| |
| x = Ae−γtcos(ω1t + φ) + |
F0 / m |
sin(ωt + φ0 + β) |
 |
| √[(ω02 − ω2)2 + 4γ2ω2) |
|
| |
| ω0 = √ |
k |
|
γ = |
b |
|
ω1 = √(ω02 − γ2) |
|
β = tan−1[ |
ω02 − ω2 |
] |
 |
 |
 |
| m |
2m |
2γω |
|
У решения есть две части: переходное и устойчивое состояние. Переходная часть, у которой есть то же самое решение как у затухающего гармонического осциллятора, тухнет по экспоненте и зависит от начальных условий. У части устойчивого состояния есть амплитуда, которая остается постоянной и не зависит от начальных условий. Таким образом, без разницы, какими были начальные условия осциллятора, он, в конечном счете, приобретет поведение, которое совершенно зависит от движущей силы.
Амплитуда, которую, в конечном счете, приобретает осциллятор, зависит от отношения движущей частоты к естественной частоте осциллятора и на факторе демпфирования. Она максимальна, когда
(ω02 − ω2)2 + 4γ2ω2
минимальна. Это происходит, когда отношение этих двух частот равно
√(1 + γ2).
Это условие известно как резонанс и результаты в большой амплитуде колебания. Когда движущая частота равняется естественной частоте, амплитуде части устойчивого состояния решения
| F0 / m |
сокращается до |
F0 / m |
 |
 |
| √[(ω02 − ω2)2 + 4γ2ω2] |
2γω |
Поскольку фактор затухания приближается к нолю, амплитуда устойчивого состояния приближается к бесконечности. Это иллюстрирует важность затухания в структурах, восприимчивых к вибрации, таких как висячие мосты и стальные здания. Без затухания структура могла распасться на куски от крошечной внешней силы правильной частоты.
Классическая демонстрация резонанса - инцидент с мостом Тэкома Нарроус. Длинные мосты теперь все разработаны с открытыми распорками поперечного сечения, чтобы рассеять часть силы ветра.
Мы рассмотрели как линейное дифференциальное уравнение второго порядка, простой гармонический осциллятор, может произвести множество поведений. В затухающем гармоническом осцилляторе мы видели показательный распад к положению равновесия с естественной периодичностью как ограничивающий случай. Определяющим фактором, который описал систему, было отношение между естественной частотой и фактором затухания. В ведомом гармоническом осцилляторе мы видели, что быстротечность привела к некоторой периодичности устойчивого состояния. Заключительное поведение системы зависело от отношения между ведущей частотой и естественной частотой (и до меньшей степени фактор затухания). Поведения, описанные выше, также сочтены в первом порядке нелинейными разностными уравнениями; квадратное сопоставление и связанное логистическое уравнение.



