Аннотация
Максименко В.Л., Иванов А.Ю. Исследование автоколебаний при моделировании гармонического осциллятора с использованием комплексов моделирования. Рассмотрены системы блочного моделирования. Исследовано моделирование уравнения гармонического осциллятора. Проведено сравнение моделирующих сред.
Общая постановка проблемы.
Колебательные процессы в технике имеют большое значение. Электромагнитные колебания лежат в основе всех современных электронных средств передачи и обработки информации.
Для облегчения понимания общих закономерностей колебательных процессов целесообразно начинать их изучение с простых и наглядных систем, например, замкнутая цепь, содержащая конденсатор и катушку индуктивности. Изменение во времени физических величин, характеризующих разные колебательные системы, описывается одинаковыми дифференциальными уравнениями.
Исследование компьютерных программ при моделировании разных способов возбуждения колебаний позволяет определить точностные и частотные характеристики программ.
Анализ архитектур моделирующих программ
На данный момент существует множество систем моделирования. Анализ научно-технической литературы показывает, что наиболее популярными являются системы моделирования DyMoLa, Dynast, Multisim, VisSim, МВТУ, MVS, SimuLink[1] Для сравнения при изучения гармонических колебаний были выбраны специализированные системы SimuLink и МВТУ.
Программный комплекс «МВТУ»[3] предназначен для исследования динамики и проектирования самых разнообразных систем и устройств. По своим возможностям он является альтернативой аналогичным зарубежным программным продуктам Simulink, VisSim и др. Удобный редактор структурных схем, обширная библиотека типовых блоков и встроенный язык программирования позволяют реализовывать модели практически любой степени сложности, обеспечивая при этом наглядность их представления. ПК «МВТУ» успешно применяется для проектирования систем автоматического управления, следящих приводов и роботов-манипуляторов, ядерных и тепловых энергетических установок, а также для решения нестационарных краевых задач (теплопроводность, гидродинамика и др.). Он широко используется в учебном процессе, позволяя моделировать различные явления в физике, электротехнике, в динамике машин и механизмов, в астрономии и т.д. Отличительной особенностью комплекса является возможность функционировать в многокомпьютерных моделирующих комплексах, в том числе и в режиме удаленного доступа к технологическим и информационным ресурсам.
ПК «МВТУ» реализует следующие режимы работы: моделирование, оптимизация, анализ, синтез, контроль и управление.
Для отечественных пользователей удобство работы с ПК «МВТУ» обусловлено русскоязычным интерфейсом и наличием обширной документации на русском языке. Учебная и демонстрационная версии ПК «МВТУ» вместе с полной документацией и набором демонстрационных примеров распространяются свободно[1]. В учебной версии есть ограничения на сложность модели: порядок дифференциальных уравнений не выше 30, а число блоков не более 100. В демонстрационной версии таких ограничений нет, но модель нельзя сохранить.
В качестве сравниваемой системы выбрана MATLAB, а точнее toolbox к нему под – Simulink. Этот выбор основан на том, что Simulink, как и МВТУ, является блочным языком программирования. Программа Simulink является приложением к пакету MATLAB. При моделировании с использованием Simulink реализуется принцип визуального программирования, в соответствии с которым, пользователь на экране из библиотеки стандартных блоков создает модель устройства и осуществляет расчеты. При этом, в отличие от классических способов моделирования, пользователю не нужно досконально изучать язык программирования и численные методы математики, а достаточно общих знаний требующихся при работе на компьютере и, естественно, знаний той предметной области, в которой он работает.
Simulink является достаточно самостоятельным инструментом MATLAB и при работе с ним совсем не требуется знать сам MATLAB и остальные его приложения. С другой стороны доступ к функциям MATLAB и другим его инструментам остается открытым и их можно использовать в Simulink. Часть входящих в состав пакетов имеет инструменты, встраиваемые в Simulink (например, LTI-Viewer приложения Control System Toolbox – пакета для разработки систем управления). Имеются также дополнительные библиотеки блоков для разных областей применения (например, Power System Blockset – моделирование электротехнических устройств, Digital Signal Processing Blockset – набор блоков для разработки цифровых устройств и т.д).
При работе с Simulink пользователь имеет возможность модернизировать библиотечные блоки, создавать свои собственные, а также составлять новые библиотеки блоков.
При моделировании пользователь может выбирать метод решения дифференциальных уравнений, а также способ изменения модельного времени (с фиксированным или переменным шагом). В ходе моделирования имеется возможность следить за процессами, происходящими в системе. Для этого используются специальные устройства наблюдения, входящие в состав библиотеки Simulink. Результаты моделирования могут быть представлены в виде графиков или таблиц.
Преимущество Simulink заключается также в том, что он позволяет пополнять библиотеки блоков с помощью подпрограмм написанных как на языке MATLAB, так и на языках С + +, Fortran и Ada.
При сравнении моделирующих программ видно, что их модульная структура практически неизменна:
- графический интерфейс ориентирован на человека и отвечает за представление математической модели в виде, понятном широкому кругу специалистов. Это могут быть блок-схемы, схемы физические принципиальные, гибридные карты состояний и пр.;
- система управления базой данных отвечает за хранение объектов составленной пользователем модели и требуемые трансформации структуры ее хранилища;
- математическое ядро берет на себя основную вычислительную нагрузку, и, в цикле, согласно заданной программе, руководствуясь готовностью аргументов и приоритетностью математических операций, обеспечивает исполнение потоков математических функций.
Разработчики моделирующих программ при создании своих продуктов не достаточно ориентируются на современные технологии модуляризации (COM, CORBA) и предпочитают выполнять реализацию самостоятельно. Все модули могут быть не просто автономными, а уже традиционно считаются независимыми программными продуктами. Наиболее простой и легкий в создании модуль - математическое ядро.
Анализ программ для моделирования динамических процессов
В тестируемой модели для разработки системных программ, в т.ч. реального времени, является модель гармонического осциллятора. Она позволит определить частоту и точные характеристики разрабатываемых программ.
В качестве исследуемой функции возьмем уравнение Ван дер Поля, амплитуда колебаний которого затухает во времени:
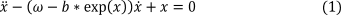
В моделировании для коэффициентов  и b будем использовать следующие значения:
и b будем использовать следующие значения:
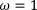

Моделирование дифференциального-алгебраического уравнения Ван-дер-Поля.
В обеих системах моделирования все элементы представлены блоками. На их базе в системах моделирования была построена схема (рис. 1, 2).
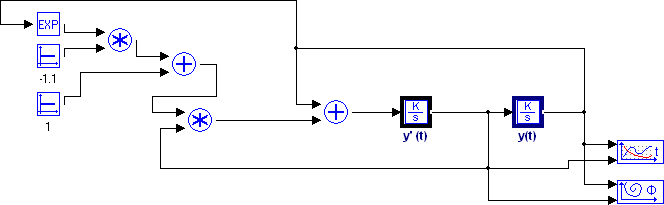
|
Рисунок 1 – Модель уравнения Ван дер Поля в системе МВТУ
|

|
Рисунок 2 – Модель уравнения Ван дер Поля в системе Simulink
|
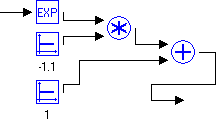
Проведем визуальное сравнение полученных схем. В целом схемы похожи, за исключением фрагмента, отвечающего за вычисление нового значения x ?.
|
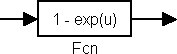
|
|
а)
|
в)
|
Рисунок 3 – Вычисление функции. а) Среда МВТУ; в) Среда Simulink
|
Из рис.3 видно, что в среде Simulink эта запись занимает всего 1 блок Fcn. В этом блоке находится наша функция, которая записана математическим выражением (2).
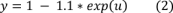
Перейдем к настройкам. Обе системы имеют широкий набор параметров. Но в МВТУ есть небольшой минус. Для замены длительности моделирования каждый раз необходимо заходить в «параметры». В Simulink, в свою очередь, на панель вынесено поле, в котором можно менять значение, не заходя в «настройки».
После построения схемы и настройки процесса моделирования получим фазовый портрет функции и временной график, результаты приведены ниже (рис. 4-7).
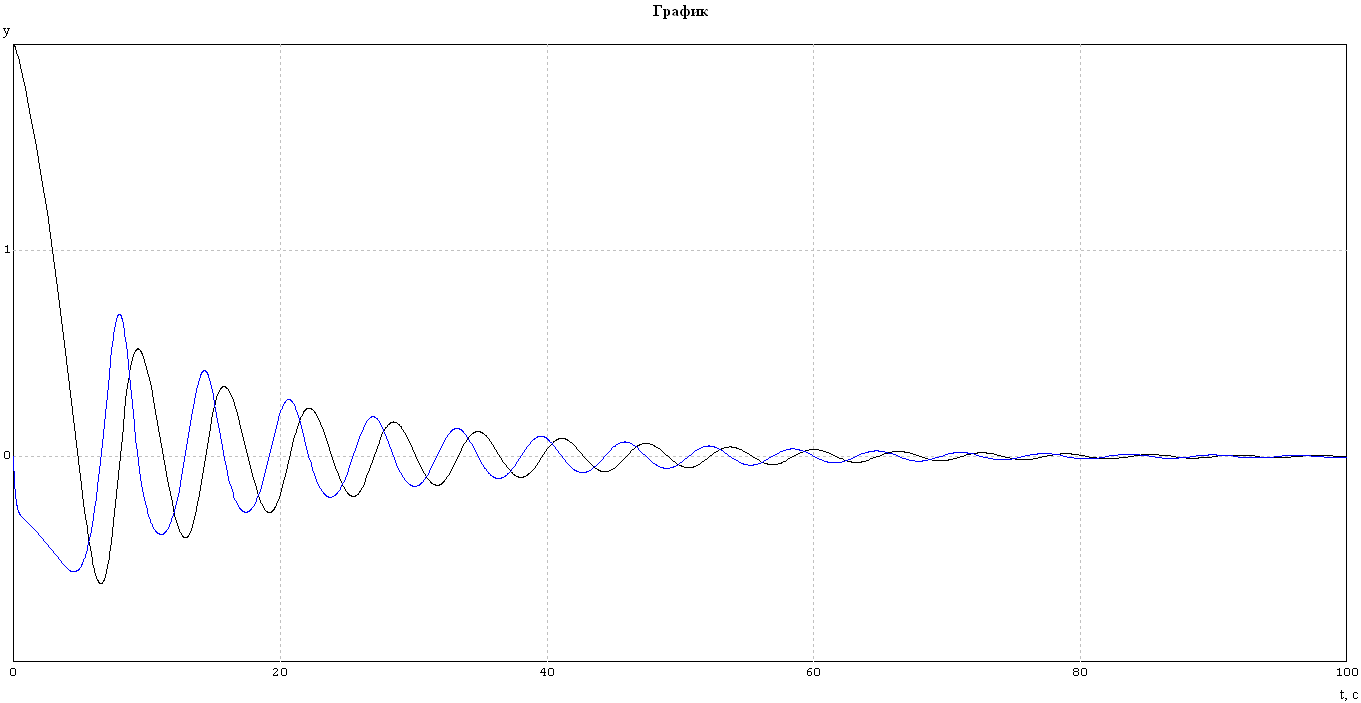
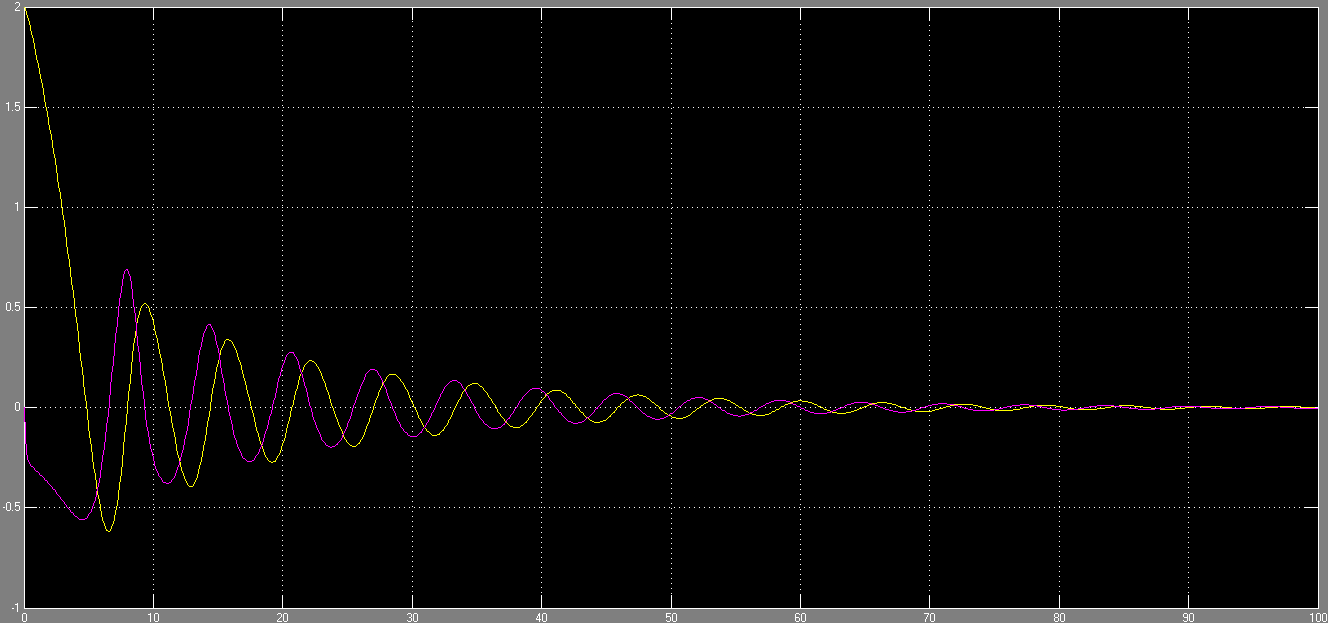
Из рисунков 4,5 и 6,7 видно, что результаты моделирования получились одинаковые.

|
Рисунок 4 – Фазовый портрет в среде МВТУ
|
|
Рисунок 5 - Временной график в среде МВТУ
|

|
Рисунок 6 – Фазовый портрет в среде Simulink
|
|
Рисунок 7 - Временной график в среде Simulink
|
Выводы
В данной работе в системах Simulink и МВТУ было промоделировано уравнение Ван дер Поля с затухающей амплитудой. Выполнены сравнительные характеристики систем моделирования Simulink и МВТУ. Все промоделированные уравнения имеют временные графики.
Так же стоит отметить, что программное обеспечение имеет характеристики, которые необходимо отметить в ходе сравнения:
- потребление ресурсов;
- быстродействие.
По окончанию моделирования МВТУ занимало почти в 2 меньше оперативной памяти. Что касается быстродействия, то SimeLink затратил на моделирование примерно 9 секунд, а МВТУ около 2 секунд. Тесты проводились на компьютере со следующими параметрами:
- ОС – Windows XP x64 edition
- Процессор – AMD Athlon 64 1.6GHz
- ОЗУ – DDR2 4 Гб
Список использованной литературы
1. Model.Exponenta.Ru — учебно-методический сайт о моделировании и исследовании систем, объектов, технических процессов и физических явлений. http://model.exponenta.ru/
2. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. М.: Мир, 1999. 685 с.
3. Сайт разработчиков ПК «МВТУ». http://mvtu.power.bmstu.ru/
4. Shampine L.F., Reichelt M.W. The MATLAB ODE Suite // SIAM J. on Scientific Computing. Vol. 18. 1997. № 1. P. 1-22.
5. Bogacki P., Shampine L.F. A 3(2) pair of Runge-Kutta formulas // Applied Mathematics Letters. Vol. 2. 1989. № 4. P. 321-325.
6. Hosea M.E., Shampine L.F. Analysis and implementation of TRBDF2 // Applied Numerical Mathematics. Vol. 20. 1996. № 1-3. P. 21-37.
7. Скворцов Л. М. Адаптивные методы численного интегрирования в задачах моделирования динамических систем // Изв. РАН. Теория и системы управления. 1999. № 4. С. 72-78.



