|
|
Рассмотрим движения движение цепочки связанных гармонических осцилляторов (рис. 1) под действием вынуждающей силы. Проводимое рассмотрение ограничим случаем, когда сила приложена к т. А колебательной системы, что для достаточно длинных цепочек не приводит, к потере общности получаемых результатов.
|
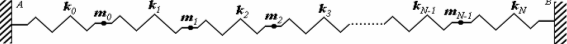
|
| Рис. 1
|
|
Система дифференциальных уравнений, описывающих движение каждого тела системы, имеет следующий вид:
|
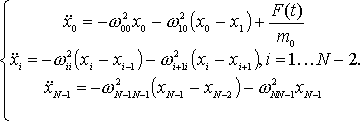
|
(1)
|
|
Решения системы (1) будем искать численно. Решение системы дифференциальных уравнений в пакете MATLAB находится в соответствие со следующим алгоритмом:
- задать вектор-функцию, возвращающую значения первых производных системы ДУ (размерность функции 2N);
- задать вектор, содержащий начальные условия (xi(0),
 i(0), i=1,2,...,N-1); i(0), i=1,2,...,N-1);
- обратиться к одной из функций, возвращающих таблицу, содержащую численное решение системы ДУ, например функции ode45;
- провести визуализацию полученных численных решений.
Описание функции, возвращающей значения первых производных системы ДУ (1), мы разместили в файле Euler2.m, листинг которого приводится ниже.
% листинг файла Euler2.m
function z=euler2(t,x)
% описание функции, возвращающей значения первых производных
global k m A Omega
N=length(m); % число тел колебательной системы
z=zeros(2*N,1);
z(1)=x(2);
z(2)=-(k(1)/m(1))*x(1)-(k(2)/m(1))*(x(1)-x(3))+F(t,A,Omega);
K=3;
for i=2:N-1
z(K)=x(K+1);
z(K+1)=-(k(i)/m(i))*(x(K)-x(K-2))-(k(i+1)/m(i))*(x(K)-x(K+2));
K=K+2;
end;
z(2*N-1)=x(2*N);
z(2*N)=-(k(N)/m(N))*(x(2*N-1)-x(2*N-3))-k(N+1)/m(N)*x(2*N-1);
function f=F(t,A,Omega)
% функция, описывающая внешнюю вынуждающую силу
f=A*sin(Omega*t);
Далее для нахождения и визуализации численного решения системы ДУ (1), описывающих систему, совершающую свободные колебания, необходимо выполнить следующую последовательность команд:
>> clear all;
>> global k m A Omega
>> N=16; % число тел колебательной системы
>> n=1:N;
>> m(n)=1; % задание масс тел
>> i=1:N+1;
>> k(i)=1; % задание жесткостей пружин колебательной системы
>> n=1:2*N;
% начальные условия
>> R0(n)=0;
>> R0(1)=0.5
>> A=0; % амплитуда внешней вынуждающей силы
>> Omega=0.0; % частота внешней вынуждающей силы
>> Tfin=50*pi; %правая граница временной сетки
>> Np=2^13-1; % число узлов временной сетки
>> [T,M]=ode45('euler2',[0:Tfin/Np:Tfin],R0);
>> subplot(4,4,1);plot(T,M(:,1));axis([0 40 -0.5 0.5]);title('n=1');
>> subplot(4,4,5);plot(T,M(:,3));axis([0 40 -0.5 0.5]);title('n=2');
>> subplot(4,4,9);plot(T,M(:,5));axis([0 40 -0.5 0.5]);title('n=3');
>> subplot(4,4,13);plot(T,M(:,7));axis([0 40 -0.5 0.5]);title('n=4');
>> subplot(4,4,2);plot(T,M(:,9));axis([0 40 -0.5 0.5]);title('n=5');
>> subplot(4,4,6);plot(T,M(:,11));axis([0 40 -0.5 0.5]);title('n=6');
>> subplot(4,4,10);plot(T,M(:,13));axis([0 40 -0.5 0.5]);title('n=7');
>> subplot(4,4,14);plot(T,M(:,15));axis([0 40 -0.5 0.5]);title('n=8');
>> subplot(4,4,3);plot(T,M(:,17));axis([0 40 -0.5 0.5]);title('n=9');
>> subplot(4,4,7);plot(T,M(:,19));axis([0 40 -0.5 0.5]);title('n=10');
>> subplot(4,4,11);plot(T,M(:,21));axis([0 40 -0.5 0.5]);title('n=11');
>> subplot(4,4,15);plot(T,M(:,23));axis([0 40 -0.5 0.5]);title('n=12');
>> subplot(4,4,4);plot(T,M(:,25));axis([0 40 -0.5 0.5]);title('n=13');
>> subplot(4,4,8);plot(T,M(:,27));axis([0 40 -0.5 0.5]);title('n=14');
>> subplot(4,4,12);plot(T,M(:,29));axis([0 40 -0.5 0.5]);title('n=15');
>> subplot(4,4,16);plot(T,M(:,31));axis([0 40 -0.5 0.5]);title('n=16');
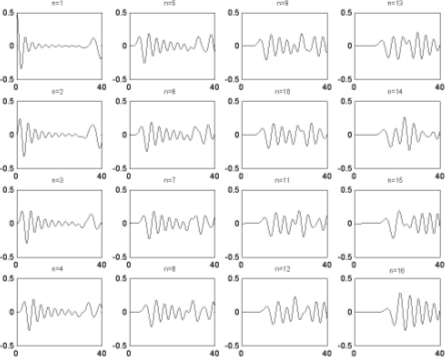
Результат выполнения приведенной выше последовательности команд представлен на рис. 2.
Одной из основных проблем численного решения ДУ и систем ДУ является проблема выбора шага интегрирования , поскольку при достаточно большом шаге интегрирования возникают неустойчивые решения, т.е. решения, погрешность которых начинает возрастать во времени экспоненциально быстро. Один из способов проверки устойчивости метода заключается в контроле величины полной энергии, которая в случае свободных колебаний должна сохраняться, поэтому для проверки правильности выбора шага интегрирования 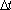 можно использовать следующий алгоритм: можно использовать следующий алгоритм:
- Задать начальные смещения и скорости тел цепочки связанных осцилляторов.
- Задать временной интервал, на котором ищется решение системы ДУ.
- Задать число точек, в которых ищется численное решение системы ДУ.
- Найти решение системы ДУ.
- Вычислить значения энергии системы связанных осцилляторов в каждый момент времени.
- Проанализировать изменение энергии системы во времени на заданном временном интервале и оценить точность выполнения закона сохранения энергии.
- При неудовлетворительной точности решения повторить пп. 3 6.
- При удовлетворительной точности решения перейти к анализу вынужденных колебаний.
|
| Рис. 2. Зависимость мгновенных значений смещения тел колебательной системы от времени
|
Как очевидно, для реализации описанного выше алгоритма необходимо уметь вычислять энергии каждого из тел системы в заданные моменты времени. Для решения данной задачи можно использовать функцию En, описание которой мы сохранили в файле En.m.
% листинг файла En.m
function E=En(N,m,k,M)
K=length(M); % число строк матрицы решений
K1=1;
for j=1:N
for i=1:K
if j>1
if j<N
e(i)=0.5*m(j)*M(i,2*j).^2+...
0.25*k(j)*(M(i,2*j-1)-M(i,2*j-3)).^2+...
0.25*k(j+1)*(M(i,2*j-1)-M(i,2*j+1)).^2;
end;
end;
if j==1
e(i)=0.5*m(1)*M(i,2)^2+0.5*k(1)*M(i,1)^2+…
0.25*k(2)*(M(i,1)-M(i,3))^2;
end;
if j==N
e(i)=0.5*m(N)*M(i,2*N)^2+0.5*k(N+1)*M(i,2*N-1)^2+...
0.25*k(N)*(M(i,2*N-1)-M(i,2*N-3))^2;
end;
end;
en(:,K1)=e';
K1=K1+1;
end;
E=en;
Для вычисления мгновенных значений энергии тел колебательной системы и ее полной энергии необходимо выполнить следующую последовательность команд:
>> clear all;
>> global k m A Omega
>> N=16;
>> n=1:N;
>> m(n)=1;
>> i=1:N+1;
>> k(i)=1;
>> n=1:2*N;
>> R0(n)=0;
>> R0(1)=0.5;
>> A=0.0;
>> Omega=0.0;
>> Tfin=50*pi;
>> Np=2^13-1;
>> [T,M]=ode45('euler2',[0:Tfin/Np:Tfin],R0);
>> E=En(N,m,k,M);
>> plot(T,E(1,:),T,E(8,:),T,E(16
>> for i=1:Np+1
s=E(i,:);
Efull(i)=sum(s);
end;
>> figure(1);plot(T,E(:,1),T,E(:,4),T,E(:,8),T,E(:,12))
>> axis([0 30 0 0.25]);
>> figure(2);plot(T,Efull)
Результаты выполнения приведенной выше последовательности команд представлены на рис. 2, 3.
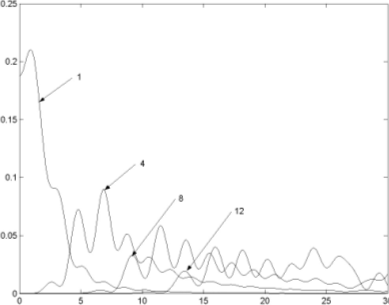
|
| Рис. 2. Мгновенные значения энергий выбранных тел колебательной системы
|
Анализ зависимости мгновенной энергии колебательной системы от времени, представленная на рис. 3, показывает, что полная энергия отклоняется от своего первоначального значения по линейному закону. При этом максимальная величина отклонения, характеризующая точность численного решения, на выбранном временном интервале не превосходит 0.24%.
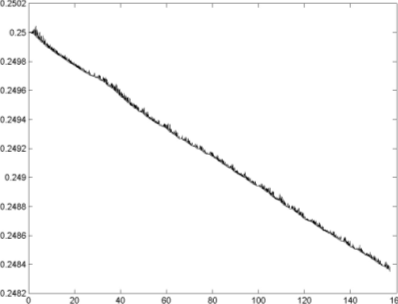
|
| Рис. 3. Зависимость полной энергии системы от времени
|
Литература
- Гетманова Е.Г., Костарев Д.Б. Резонансные явления в системе связанных осцилляторов// Электромагнитные волны и электронные системы. 2009. Т. 6. № 5.
- Коткин Г.Л., Сербо В.Г. Сборник задач по классической механике. М.: Наука, 1977.
- Ландау Л.Д., Лифшиц Е.М. Механика. М.: Наука, 2000.
- Крауфорд Ф. Волны. М.: Наука, 1974.
- Гулд Х., Тобочник Я. Компьютерное моделирование в физике. М.: Мир, 1990. С. 220.
|
|
|



