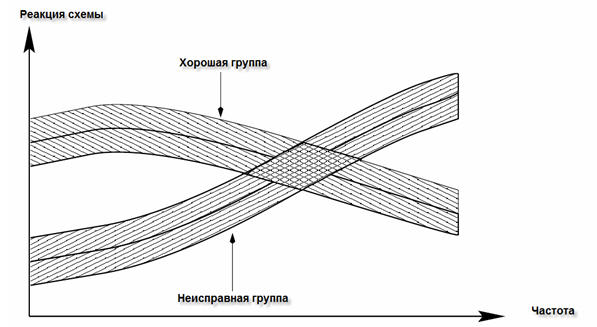
Рисунок 1 - Иллюстрация хорошей и неисправной группы
Источник: Google Академия
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.29.4092
Управляемые неисправности аналоговых и смешанных сигналов тестирования требуют быстрых техник моделирования неисправностей. Проблемой, которая не была эффективно решена данным исследованием, является то, что параметры схем имеют пределы допусков. В этой статье мы предлагаем представить варьирующиеся параметры как интервалы, и представить эффективный алгоритм – базирующийся на анализе интервалов и формуле Хаусхолдера – для определения худшей реакции, связывающей правильную и ошибочную линейную схему с параметрическими вариациями. Наш подход занимает процессорное время сопоставимое с одним номинальным моделированием схемы, и всегда производит правильные и стабильные результаты. Алгоритм был реализован в SPICE3F5. Экспериментальные результаты показывают приемлемую точность.
В последние несколько лет, встроенные схемы с аналоговыми и со смешанными сигналами стали важнее, из-за быстрой сходимости вычислений в бытовой электронике и связи. С ранних 90-х, средний темп роста рынка микросхем со смешанными сигналами составлял от 15% до 20% в год [3]. Все более возрастающий уровень сложности интеграции и сокращение жизненного цикла товаров – микросхем и систем со смешанными сигналами создали множество проблем в разработке и тестировании. Среди них, тестирование работоспособности аналоговых схем, то есть, аналоговое тестирование, является одним из наиболее важных вопросов. Определено, что влияние аналогового тестирования на время выхода на рынок и конечной стоимости схемы становится все более значимым. Моделирование аналоговых неисправностей является ключевым вопросом в аналоговом тестировании, с приложениями выбора теста, анализом покрытия ошибок [22], и дизайном для тестирования [14,27]. Некоторые исследовательские усилия были направлены на разработку стандартных аналоговых или со смешанными сигналами симуляторов, таких как SPICE[7], ELDO [19], и Saber [4] для выполнения моделирования неисправностей. Эта линия исследований преследуется рядом проблем. Во-первых, параметры аналоговых схем связаны с допусками в диапазонах. Только параметрические изменения, которые вынуждают производительность схемы быть за пределами существующих спецификаций, считаются неисправностями. В результате, реакции для работоспособных и неисправных схем связывают в группы, которые называются хорошими(реакция) группами и неисправными(реакция) группами соответственно. Это проиллюстрировано на рис. 1.

Другой относящийся вопрос возникает в моделировании смешанных сигналов. Неизвестные состояния в цифровой части приводят к параметрическим допускам в аналоговой части, которые непосредственно не могут быть обработаны большинством схемных симуляторов. Кроме того, в большинстве обычных схемных симуляторов встречаются численные сложности при моделировании схемы, которая содержит замыкания и обрывы. Проблема усугубляется еще и большим количеством неисправностей, которые должны быть промоделированы. Были предложены методы ускорения моделирования неисправностей линейных аналоговых схем около 20 лет назад [21,23] и недавно [16,25]. Однако, эти методы не обращаются к параметрическим допускам. Насколько нам известно, Pahwa и Rohrer, были первыми, кто эффективно решил моделирование неисправностей линейных схем с параметрическими допусками [18]. Номинальная чувствительность анализа использовалась для оценки параметров в наихудших условиях. Неисправные группы затем аппроксимируются от хорошей группы, и результирующие группы называются группы неисправностей. Тем не менее, основное предположение, что параметр в наихудших условиях остается неизменным даже при неисправности (называется допуском группы неисправности) не имеет места. Как следствие, группа неисправностей может значительно отличаться от неисправной группы. Кроме того, не существует метода проверки, удовлетворяет ли данная схема допуску группы неисправностей.
Наиболее широко используется подход к изменениям параметров модели в методе Монте Карло. С этой техникой моделирование повторяется для случайных комбинаций значений, выбранных из диапазона каждого параметра. К сожалению, точное определение границ поведения схемы требуют большого количества моделирований, для того чтобы быть эффективным. Метод становится предельно дорогой для моделирования неисправностей, начиная с момента, когда метод Монте Карло требует повторений случайно выбранного процесса для каждой неисправности. Были предложены улучшения для уменьшения времени моделирования, используя индуктивный анализ ошибки и поведенческое моделирование [6]. Однако, не существует систематических методов для извлечения поведенческих (неисправность) моделей из моделей транзисторного уровня(неисправность). Недавно, Spinks и Bell предложили использование метода Монте Карло для оценки параметров в худшем случае, и затем аппроксимировали неисправные реакции, выполняя моделирование на неисправных схемах и используя те же параметры в худшем случае [22]. Этот метод страдает от того же самого недостатка, как и подход групп неисправностей вследствие выхода параметров из зоны допустимых значений. В этой статье мы представляем быстрый, правильный и консервативный подход для моделирования неисправностей в частотной области линейных аналоговых схем и систем с изменениями параметров. Большой класс схем и систем, широко используемых в видео и обработке изображений, обработке цифровых сигналов, контроле, коммуникациях и многих других приложениях попадают в эту категорию. Далее, недавние исследования показали, что неисправности которые изменяют рабочую точку транзисторной аналоговой схемы могут быть легко обнаружены недорогим DC тестированием или контролем тока электропитания, тогда как большинство сложных для обнаружения неисправностей это те, которые причиняют отклонения в производительности[5].
Именно на этот класс линеаризовавших аналоговых схем нацелено наше исследование. Эта работа детализирует наш подход и представляет аналог опытного образца программы моделирующей неисправности, использующий предложенную технику. Интервал базирующийся на структуре обращения с изменениями параметров представлен в разделе 2. В Разделе 3, используя эту структуру, уравнения схемы сформулированы через Обобщенную MNA формулировку (GNA) рассматриваются как ряд линейных уравнений интервала, и аналоговых ошибок смоделированных как изменения интервалов. Вычисление количества хороших групп для решения набора линейных уравнений интервалов. Недавний алгоритм с этой целью приведен в разделе 4. Раздел 5 показывает, как группы ошибок могут быть получены с очень незначительной вычислительной стоимостью от хорошей группы используя Householder’s формулы. Выполнение и экспериментальные результаты описаны в Разделе 6. Раздел 7 завершает статью.
Границы, основанные на интервалах были представлены для моделирования неисправностей линейных аналоговых схем в частотной области и систем с изменяемыми параметрами. Наш подход имеет несколько основных черт которые отличают его от предыдущих подходов.
Наш метод очень быстрый, и сравним с регулярным номинальным моделированием схемы. Предположим, что есть m-пробных моделирований методом Монте Карло для n неисправностей, предложенный метод моделирования неисправностей(используя формулу Householder) получает теоретическое ускорение O(mn) сравнивая с методом Монте Карло.
Наш метод точен и консервативен. Неисправные группы вычисленные нашим методом всегда содержат точные неисправности групп. Это свойство обеспечивает правильность и надежность использования нашего метода моделирования неисправностей в выборе тестов, анализ покрытия неисправностей и дизайн для теста. Далее, если диапазоны допусков параметров относительно узкие, наш метод вводит очень узкие ограничения. Для тех неисправностей, которые вносят большие изменения в производительности схемы, мы отмечаем что они могут быть легко обнаружены недорогим DC тестированием и контролем за силой тока(не требуется AC тестирование).
С того момента, как моделирование неисправностей выполнено по формуле Householder’s, множество особенных проблем связанных с прямым использованием обычных моделирующих неисправности пакетов – не существует.
Так как моделирование неисправностей происходит на уровне схемы, нет отображения неисправностей на поведенческом уровне, как того требуют ЧЕРНОВИКИ [16], или поведенческое моделирование неисправностей [6,8], которое должно быть. Это обеспечивает покрытие ошибок неизменным.