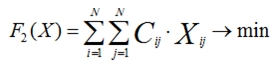УДК 004.023

ИСПОЛЬЗОВАНИЕ АЛГОРИТМА МУРАВЬИНОЙ КОЛОНИИ ДЛЯ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНОГО МАРШРУТА ДОСТАВКИ ГРУЗОВ

Мурзин Б.П., Светличная В.А

Донецкий национальный технический университет

кафедра автоматизированных систем управления

e-mail: bogdan.murzin@gmail.com

Аннотация:

Мурзин Б.П., Светличная В.А. Использование алгоритма муравьиной колонии для определения оптимального маршрута доставки грузов. В данной статье рассмотрено применение алгоритма муравьиной колонии для оптимального распределения товаров между автомобилями и построение оптимальных маршрутов для каждого из них. Предложен алгоритм с использованием нескольких муравьиных колоний.

Введение

На сегодняшний день грузоперевозки являются неотъемлемой частью жизнедеятельности людей. Грузы можно перевозить в любое место, независимо от их объёма и габаритов. Вариантов грузоперевозки предоставляется достаточно. Автоматизация системы построения маршрутов является необходимостью для предприятия при его росте. Внедрение такой системы является экономически выгодным решением, так как это ускоряет процесс работы диспетчера, минимизирует влияние человеческого фактора, ведет к сокращению простоя автомобилей под загрузкой и разгрузкой, эффективному использованию подвижного состава.

Общая постановка проблемы

Задача решается в условиях центрального склада фармацевтической компании. За данным складом закреплена сеть аптек, на которые ежедневно выполняется поставка лекарственных и сопутствующих средств, в соответствии с составленным заказом. Заказ в каждой аптеке формируется каждое утро и высылается на склад, следовательно, задача составления плана маршрута для автомобилей решается каждый день. Система должна учитывать ограниченную грузоподъемность каждого транспортного средства, а так же факт несовместимости перевозки различных групп товаров в одном кузове. Иногда заказ от аптеки может не поступать, тогда данная аптека исключается из маршрутного листа и необходимо произвести перерасчет маршрута. В связи с этим нужно использовать методы, способные быстро решать поставленную задачу и динамично подстраиваться под ее условия.

С помощью технологии геоинформационной системы (ГИС) предоставляется карта автомобильных дорог, на которой указаны пункты, соответствующие аптекам. Складу приписан парк автотранспорта, характеризующийся количеством автомобилей определенного типа и их массо-габаритными параметрами. Заявки от потребителей, являющиеся входной информацией, поступают на склад из торговой системы. Матрица взаимных расстояний между объектами развоза, также поступающая на вход системы, рассчитывается средствами ГИС.

Решение поставленной задачи развоза товаров осуществляется в два этапа. На первом этапе решается задача разбиения региона на компактные зоны обслуживания - направления (группирование объектов-получателей для каждого маршрута). Эту задачу будем называть задачей кластеризации. На втором этапе решается задача нахождения оптимального по расстоянию порядка объезда получателей для каждого маршрута (маршрутизация).

При решении задачи необходимо учитывать реалии и ограничения, с которыми перевозчики сталкиваются на практике. Существующая региональная дистрибьюторская сеть такой компании характеризуется, как правило, разветвленной сетью автодорог разного качества, сотнями объектов развоза, большим разбросом расстояний между поставщиками и получателями (от единиц до сотен километров), небольшими объемами складских помещений у получателей товара, ограниченными возможностями транспортного парка. Таким образом, разработка эффективных маршрутов и проектов планов перевозок способствует своевременному и бесперебойному выполнению поставок продукции и эффективному взаимодействию поставщиков и получателей.

В данной работе рассмотрен метод решения задачи маршрутизации транспортных грузоперевозок с использованием алгоритма муравьиной колонии. Объектом оптимизации данного алгоритма является массив маршрутов объезда точек заказчиков парком грузовых автомобилей с фиксированной грузоподъемностью. Сеть дорог представлена в виде взвешенного графа, узлами которого являются координаты аптек.

Муравьиный алгоритм — один из эффективных полиномиальных алгоритмов для нахождения приближённых решений задачи маршрутизации. Суть подхода заключается в анализе и использовании модели поведения муравьёв, ищущих пути от колонии к источнику питания и представляет собой метаэвристическую оптимизацию. В реальном мире, муравьи (первоначально) ходят в случайном порядке и по нахождению продовольствия возвращаются в свою колонию, прокладывая феромонами тропы. Если другие муравьи находят такие тропы, они, вероятнее всего, пойдут по ним. Вместо того, чтобы отслеживать цепочку, они укрепляют её при возвращении, если в конечном итоге находят источник питания. Со временем феромонная тропа начинает испаряться, тем самым уменьшая свою привлекательную силу. Чем больше времени требуется для прохождения пути до цели и обратно, тем сильнее испарится феромонная тропа. На коротком пути, для сравнения, прохождение будет более быстрым и как следствие, плотность феромонов остаётся высокой. Испарение феромонов так же имеет свойство избегания, стремления к локально-оптимальному решению. Если бы феромоны не испарялись, то путь, выбранный первым, был бы самым привлекательным. В этом случае, исследования пространственных решений были бы ограниченными. Таким образом, когда один муравей находит (например, короткий) путь от колонии до источника пищи, другие муравьи, скорее всего пойдут по этому пути, и положительные отзывы в конечном итоге приводят всех муравьёв к одному, кратчайшему, пути.

В данной статье рассмотрен алгоритм с применением двух типов муравьёв для оптимизации двух целевых функций и нахождения оптимального решения.

Решение задачи

В условиях данной задачи в роли муравья выступает автомобиль, который начиная движение со склада должен пройти по всем указанным точкам, ребром является дорожная сеть между двумя аптеками, а вес ребра определяет расстояние между ними.

Моделирование поведения муравьёв связано с распределением феромона на тропе - ребре графа. При этом вероятность включения ребра в маршрут отдельного муравья пропорциональна количеству феромона на этом ребре, а количество откладываемого феромона пропорционально длине маршрута. Чем короче маршрут, тем больше феромона будет отложено на его рёбрах, следовательно, большее количество муравьёв будет включать его в синтез собственных маршрутов. Моделирование такого подхода, использующего только положительную обратную связь, приводит к преждевременной сходимости - большинство муравьёв двигается по локально оптимальному маршруту. Избежать этого можно, моделируя отрицательную обратную связь в виде испарения феромона. При этом если феромон испаряется быстро, то это приводит к потере памяти колонии и забыванию хороших решений, с другой стороны, большое время испарения может привести к получению устойчивого локального оптимального решения.

Целевая функция является составной, т.е. состоит из двух частей: числа автомобилей (1), необходимых для выполнения задачи и общего времени в пути (2). Минимизация количества поездок является более привилегированной, чем минимизация времени.

F_­1(v) = v> min (1)

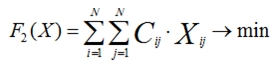(2)

где С_ij – матрица расстояний между точками, X_ij – матрица переходов, v – количество автомобилей.

Основная идея алгоритма – это использование двух типов муравьев, один минимизирует количество автомобилей для выполнения доставки, а второй – время в пути. Первый тип связывает точки доставки с автомобилем (кластеризация), а далее другой тип муравьев определяет оптимальный маршрут минимизируя общую длину маршрута.

План алгоритма состоит в следующем:

- инициализация троп феромона и параметров, создавая начальное решение;

- улучшение решения каждого муравья, пока оно возможно:

- использование локального поиска;

- использование двух следующих схем для локального поиска: вставка/обмен точек, обмен подпутей;

- обновление элитных муравьев;

- если не произошло изменений в элитных муравьях и решениях за последние 10 итераций, то начать сначала, иначе – обновить тропы;

- вернуть лучшее решение.

В рамках данной статьи будет рассмотрен первый шаг, который включает создание начального решения и описание процесс реинициализации.

Тропы проинициализированы используя начальное решение, процедура которого состоит из двух стадий. В первой клиенты случайным образом связываются один за другим с автомобилями с заданным количеством (v), пренебрегая грузоподъемностью. На второй стадии создается маршрут для каждого автомобиля, итеративно добавляя связанных клиентов. Начальное решение играет важную роль в метаэвристических алгоритмах, но в алгоритмах муравьиной колонии его влияние не так велико, поэтому для инициализации не будет использована трудоемкая процедура.

Мы используем два типа муравьев: автомобильные и маршрутные. Мощность тропы автомобильного муравья представляет вероятность для клиента i, что он будет обслужен автомобилем k. Мощность тропы маршрутного муравья является вероятностью посещения клиента j сразу после клиента i. Пусть L – значение целевой функции (т.е. общая длина маршрута) в начальном решении. Изначально будет установлено , при i=1..n, j=1..k, ilj. На втором шаге мощность тропы будет переинициализирована 5 раз. Используется значение целевой функции с наилучшим значением L_best, l1_ik и l2_ij устанавливаются равными 1/ L_best.

Создание решения муравьём

Связывание точек с автомобилями с учетом того, что грузоподъемность автомобиля не будет превышена. Пусть n – количество клиентов, l - множество еще не обслуженных клиентов, C_k – множество клиентов обслуживаемых автомобилем k, v – количество автомобилей, Q – грузоподъемность каждого автомобиля, AC_k – доступная грузоподъемность автомобиля k.

Приведенная ниже процедура представляет шаги для связывания точек с автомобилями:

- инициализация множеств и установление грузоподъемности l={1,2,…,n}, C_k=0, AC_k=Q, k=1..v;

- случайный выбор еще не привязанного клиента i и назначение его автомобилю, удаление клиента i из множества l;

- пусть l – количество допустимых автомобилей. Автомобиль доступен для связывания с клиентом i, если грузоподъемность AC_k более или равна спросу клиента. Автомобиль который будет обслуживать клиента i определяется по правилу 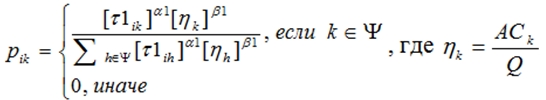(3):

(3)

Здесь l_k - локальная видимость, определяет привлекательность клиента для данного автомобиля. Параметры l1, l1 отражают относительное влияние мощности тропы и локальной видимости. Когда автомобиль выбран, значение AC_k обновляется, а клиент добавляется в множество C_k;

- если l=0, то алгоритм заканчивается, иначе – возвращаемся на шаг выбора.

Существует вероятность получения невыполнимого решения на шаге 3 из-за ограниченной грузоподъемности автомобиля. В частности во время привязывания последнего клиента может выйти так, что ни один автомобиль не сможет обслужить клиента, т.е. l=0. В этом случае шаги 1-4 повторяются где клиенты из l упорядочены по убыванию спроса, пока не будет получено допустимое решение.

Создание маршрута для каждого автомобиля

После того, как точки связаны с автомобилями, происходит решение задачи коммивояжера для каждого автомобиля. Муравей начинает движение со склада и последовательно строит решение путем выбора следующего клиента j из множества доступных клиентов, Re. Привлекательность посещения клиента j сразу после клиента i определяется как l_ij=[ l2_ij]^l2[s(i,j)]^l2. Параметр l2 представляет влияние мощности тропы, а l2 – сохранение текущего значения. Вероятность перехода от клиента i к клиенту j определяется по формуле 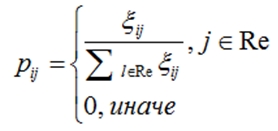(4):

(4)

Действие продолжается пока не будет найден маршрут, а потом повторяется для остальных автомобилей.

Выводы

В результате проведения исследования была рассмотрена задача маршрутизации транспорта с использованием мульти-колониальных муравьиных систем (MACS-VRP) которая использует одну муравьиную колонию с двумя типами муравьёв и феромона, а так же задача маршрутизации с учетом грузоподъемности (CVRP). Разработан алгоритм, позволяющий для заданного парка грузовых автомобилей произвести кластеризацию клиентских точек и проложить маршруты минимизируя их общую протяженность.

Литература

1. Yuvraj Gajpal , Abad P.L. Multi-ant colony system for a vehicle routing problem: European Journal of Operational Research, 2008.l16с.

2. D. Angus, C. Woodward Multiple objective ant colony optimization: Springer Science, 2008.l17с.

3. A.E. Rizzoli, F. Oliverio Ant Colony Optimization for vehicle routing problems: Istituto Dalle Molle di Studi sull’Intelligenza Artilciale, 2009.-50с.

4. Ines A. Ant Colony Optimization for Multi-objective Optimization Problems: National School of Computer Sciences, 2010.l8c.