В данной статье рассмотрен алгоритм с применением двух типов муравьёв для оптимизации двух целевых функций и нахождения оптимального решения.

Целевая функция является составной, т.е. состоит из двух частей: числа автомобилей, необходимых для выполнения задачи и общего времени в пути. Минимизация количества поездок является более привилегированной, чем минимизация времени.

Основная идея алгоритма – это использование двух типов муравьев, один минимизирует количество автомобилей для выполнения доставки, а второйя – время в пути. Первый тип связывают точки доставки с автомобилем (кластеризация), а далее другой тип муравьев определяет оптимальный маршрут минимизируя общую длину маршрута.

План алгоритма состоит в следующем:

Шаг 1. Инициализация троп феромона и параметров, создавая начальное решение, установление счетчика count=1.

Шаг 2. Улучшение каждого решения муравья, пока оно возможно:

1. Использование локального поиска.

2. Использование двух следующих схема для локального поиска:

a. Вставка/обмен клиентов,

b. Обмен подпутей.

3. Обновление элитных муравьев.

4. Если не произошло изменений в элитных муравьях и решениях за последние 10 итераций, то увеличить count на 1, иначе – обновить тропы.

Шаг 3. Вернуть лучшее решение.

1. Начальное решение и реинициализация троп.

Тропы проинициализированы используя начальное решение, процедура которого состоит из двух стадий. В первой клиенты случайным образом связываются один за другим с v автомобилями, пренебрегая грузоподъемностью. На второй стадии маршрут создается для каждого автомобиля, итеративно добавляя связанных клиентов. Начальное решение играет важную роль в метаэвристических алгоритмах, но в алгоритмах муравьиной колонии его влияние не так велико, поэтому для инициализации не будет использована трудоемкая процедура.

Мы используем два типа муравьев: автомобильные и маршрутные. Мощность тропы автомобильного муравья представляет вероятность для клиента i, что он будет обслужен автомобилем k. Мощность тропы маршрутного муравья является вероятностью посещения клиента j сразу после клиента i. Пусть L – значение целевой функции(т.е. общая длина маршрута) в начальном решении. Изначально будет установлено , при i=1..n, j=1..k, ilj. На втором шаге мощность тропы будет переинициализирована 5 раз. Используется значение целевой функции с наилучшим значением L_best, l1_ik и l1_ij устанавливаются равными 1/ L_best.

2. Создание решения муравьём.

2.1. Связывание клиентов с автомобилями с учетом того, что грузоподъемность автомобиля не будет превышена.

Пусть

n – количество клиентов

l - множество еще не обслуженных клиентов

C_k – множество клиентов обслуживаемых автомобилем k

v – количество автомобилей

Q – грузоподъемность каждого автомобиля

AC_k – доступная грузоподъемность автомобиля k

Приведенная ниже процедура представляет шаги для связывания клиентов с автомобилями:

1. Инициализация множеств и установление грузоподъемности

l={1,2,…,n}, C_k=0, AC_k=Q, k=1..v

2. Случайный выбор еще не привязанного клиента i и назначение его автомобилю, удаление клиента i из множества l.

3. Пусть l – количество допустимых автомобилей. Автомобиль доступен для связывания с клиентом i, если грузоподъемность AC_k более или равно спроса клиента. Автомобиль который будет обслуживать клиента i определяется по правилу:

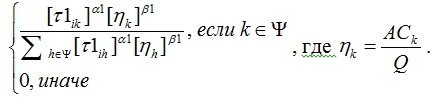
Здесь l_k - локальная видимость, определяет привлекательность клиента для данного автомобиля. Параметры l1, l1отражают относительное влияние мощности тропы и локальной видимости. Когда автомобиль выбран, значение AC_k обновляется, а клиент добавляется в множество C_k.

4. Если l=0, то алгоритм заканчивается, иначе – возвращаемся на шаг 2.

Существует вероятность получения невыполнимого решения на шаге 3 из-за ограниченной грузоподъемности автомобиля. В частности во время привязывания последнего клиента может выйти так, что ни один автомобиль не сможет обслужить клиента, т.е. l=0. В этом случае шаги 1-4 повторяются где клиенты из l упорядочены по убыванию спроса, пока не будет получено допустимое решение.

2.2. Создание маршрута для каждого автомобиля

После того, как клиенты связаны с автомобилями, происходит решение задачи коммивояжера для каждого автомобиля. Муравей начинает движение со склада и последовательно строит решение путем выбора следующего клиента j из множества доступных клиентов, Re. Изначально Re. Привлекательность посещения клиента j сразу после клиента i определяется как l_ij=[ l2_ij]^l2[s(i,j)]^l2. Параметр l2 представляет влияние мощности тропы, а l2 – сохранение текущего значения. Вероятность перехода от клиента i к клиенту j определяется по формуле:

Действие продолжается пока не будет найден маршрут, а потом повторяется для остальных автомобилей.

3. Локальный поиск

После создания решения муравьем оно улучшается локальным поиском. Для этого мы воспользуемся методом 2-opt, а так же методы вставки/обмена клиентов и обмена подпутей. Последние два используются итеративно пока не улучшат решение. Лучшее решение вставки/обмена будет использовано как начальное в методе обмена подпутей, а на следующей итерации для метода вставки/обмена начальным будет лучшее решение обмена подпутей. Так продолжается, пока эти действия не улучшат решение. Экспериментально определено, что решение находится после 3-4 итераций.

3.1. Локальный поиск 2-opt

Данный вид локального поиска является известным в задаче коммивояжера и сводится к удалению двух рёбер из тура и вставке двух новых рёбер, не нарушающих корректности решения (в случае 2-opt вставляемые рёбра определены однозначно). Тур считается локальным минимумом, если в нём не существует ни одной пары рёбер, замена которых привела бы к улучшению решения. Таким образом, и размер окрестности, и сложность эвристики составляют O(m²), где m — это число кластеров.

3.2. Вставка/обмен клиента

1. Операция вставки: Клиент i удаляется с его позиции и вставляется во все маршруты(включая исходный). Грузоподъемность проверяется перед вставкой клиента в маршрут. По условию задачи каждый автомобиль должен обслужить как минимум одного клиента. Исходя из этого, вставка клиента осуществляется только когда клиентов на маршруте более одного.

2. Операция обмена: В этой операции клиент i (из маршрута p) сдвигается на другой маршрут q, а клиент j маршрута q сдвигается на маршрут p. Клиенты вставляются на лучшие места других маршрутов.

Для оптимизации перед операцией вставки/обмена определим некоторое число e, которое будет определять количество соседей клиента i, N_e(i) будет содержать e ближайших соседей (по расстоянию). Операция обмена между клиентами i и j выполняется только в случае, если как минимум один из e соседей клиента i обслуживается маршрутом q и как минимум один из соседей клиента j обслуживается маршрутом p. Кроме того, вставка клиента i на маршрут q выполняется только тогда, когда e соседей клиента i обслуживаются маршрутом q.

План локального поиска:

1. Инициализация l ={1..n}

2. Случайный выбор клиента, определение клиента i маршрута p для оценки и удаление его из множества l.

3. Выполнение вставки клиента i для определения лучшей позиции вставки и оценки общей длины маршрута результирующего решения.

4. Рассмотрение обмена клиента i с каждым клиентом j. Обмен должен удовлетворять условиям грузоподъемности. Определение лучшего клиента для обмена j и соответствующего решения после выполнения обмена.

5. Выбор лучшего решения на шагах 3 и 4 и сохранение, если оно является лучше текущего решения.

6. Если l=0, то окончить поиск, иначе вернуться к шагу 2.

Операция вставки имеет сложность O(n²). Операция обмена рассматривает обмен одного клиента с каждым клиентом другого маршрута, следовательно, всего n*(n-n/v) возможных пар обмена.

3.3. Операция обмена подпутей

Операция обмена/вставки определяет сдвиг заданного клиента на другой маршрут. Операция обмена подпутей может сдвигать более одного клиента на другой маршрут. Пусть S={R₁, R₂,…, R_p,…, R_q,…, R_v-1,R_v} является решением задачи. Схема обмена подпутей берет пути R_p, R_q и переопределяет их в Rl_p, Rl_q для создания нового решения S={R₁, R₂,…, Rl_p,…, Rl_q,…, R_v-1,R_v}. Рассмотрим подпуть (e,…,f) принадлежащий маршруту R_p и подпуть (g,…,h) принадлежащий маршруту R_q. Новый маршрут Rl_p получен заменой (e,…,f) на (h,…,g) или на обритный (h,…,g). Аналогично получается маршрут Rl_q. Так же используется критерий соседства, обмен подпути (e,…,f) на (g,…,h), происходит только если клиент f находится среди 15 ближайших соседей клиента g.

Каждый возможный подпуть маршрутов R_p , R_q доступен для обмена и лучшая пара подпутей выбирается для создания Rl_p, Rl_q. Пусть l_i представляет непосредственного предшественника i-го клиента, а l_i – преемника, тогда общая длина пути вычисляется следующим образом:

cost(Sl)=cost(S)-c(l_e,e)-c(f, l_f)-c(l_g,g)- c(h, l_h)+

min{(c(l_e,g)+c(h, l_f)),(c(l_e,h)+ c(g,l_f))}+min{(c(l_g,e)+c(f, l_h)),(c(l_g,f)+ c(e, l_h))}.

Всего получается v*(v-1) комбинаций автомобилей для обмена подпутей. Предполагая, что n клиентов обслужены v автомобилями, всего будет n/v*(n/v-1)/2 подпутей в маршруте. Сложность метода равна O(v²)*O(n²/v²) *O(n²/v²)=O(n⁴/v²)

4. Обновление элитных муравьев

Было использовано l элитных муравьев которые отличаются от остальных. Они обновляются путем сравнения существующего и текущего решений. Если текущее решение лучше существующего, то оно сохраняется на место существующего.

5. Обновление мощности троп

Мощность автомобильных и маршрутных троп обновляется используя элитных муравьев. Автомобильные тропы обновляются по следующему правилу:

i=1..n; k=1..v, где

Здесь l – стойкость феромона, L^l-длина пути в решении найденном l-м элитным муравьем, L^*-длина пути в лучшем решении.

Аналогично происходит изменение феромона l2_ij.