Данная статья носит реферативный характер,содержание в значительной мере основано на материалах,размещённых некогда в журнале Exponenta Pro .Их автор, С .Штовба, любезно дал согласие на использование и развернутое цитирование своих результатов.

1. Введение

2. Биологические принципы поведения муравьиной колонии

3. Муравьиные алгоритмы

Немного из истории создания муравьиных алгоритмов

Концепция муравьиных алгоритмов

Обобщённый алгоритм

Этапы решения задачи при помощи муравьиных алгоритмов

4. Применение муравьиных алгоритмов для задачи коммивояжёра

Муравьиный алгоритм для задачи коммивояжёра в псевдокоде

5. Области применения и возможные модификации

6. Достоинства и недостатки муравьиных алгоритмов

Достоинства

Недостатки

7. Источники

1.Введение

В последние годы интенсивно разрабатывается научное направление с названием «Природные вычисления» (Natural Computing),объединяющее математические методы, в которых заложены принципы природных механизмов принятия решений. Эти механизмы обеспечивают эффективную адаптацию флоры и фауны к окружающей среде на протяжении нескольких миллионов лет.

Среди так называемых "Soft computing techniques", разработанных за последние десять лет для трудно решаемых задач дискретной оптимизации, числятся

 Генетические алгоритмы (GAs)
Основываются на естественном отборе и генетике

 Муравьиные алгоритмы (Ant Colony Optimization - ACO, Ant Systems - AS)
Моделируют поведение муравейника

Имитация самоорганизации муравьиной колонии составляет основу муравьиных алгоритмов оптимизации. Колония муравьев может рассматриваться как многоагентная система, в которой каждый агент (муравей) функционирует автономно по очень простым правилам. В противовес почти примитивному поведению агентов, поведение всей системы получается на удивление разумным.

Муравьиные алгоритмы серьезно исследуются европейскими учеными с середины 90-х годов. На сегодняшний день уже получены хорошие результаты для оптимизации таких сложных комбинаторных задач, как задача коммивояжера, задача оптимизации маршрутов грузовиков, задача раскраски графа, квадратичная задача о назначениях, задача оптимизации сетевых графиков, задача календарного планирования и многие другие. Особенно эффективны муравьиные алгоритмы при динамической оптимизации процессов в распределенных нестационарных системах, например, трафиков в телекоммуникационных сетях.

2.Биологические принципы поведения муравьиной колонии

Муравьи относятся к социальным насекомым, образующим коллективы. Коллективная система способна решать сложные динамические задачи по выполнению совместной работы, которая не могла бы выполняться каждым элементом системы в отдельности в разнообразных средах без внешнего управления, контроля или координации. В таких случаях говорят о роевом интеллекте (Swarm intelligence), как о замысловатых способах кооперативного поведения, то есть стратегии выживания.

Одним из подтверждений оптимальности поведения муравьиных колоний является тот факт, что сеть гнёзд суперколоний близка к минимальному остовному дереву графа их муравейников.

Основу поведения муравьиной колонии составляет самоорганизация, обеспечивающая достижения общих целей колонии на основе низкоуровневого взаимодействия. Колония не имеет централизованного управления, и её особенностями являются обмен локальной информацией только между отдельными особями (прямой обмен - пища, визуальные и химические контакты) и наличие непрямого обмена, который и используется в муравьиных алгоритмах. Таким образом, в общем случае рассматриваются слепые муравьи, не способные чувствовать близость пищи.

Непрямой обмен - стигмержи (stigmergy), представляет собой разнесённое во времени взаимодействие, при котором одна особь изменяет некоторую область окружающей среды, а другие используют эту информацию позже, когда в неё попадают. Биологи установили, что такое отложенное взаимодействие происходит через специальное химическое вещество - феромон (pheromone), секрет специальных желёз, откладываемый при перемещении муравья. Концентрация феромона на пути определяет предпочтительность движения по нему.

Адаптивность поведения реализуется испарением феромона, который в природе воспринимается муравьями в течение нескольких суток. Мы можем провести некоторую аналогию между распределением феромона в окружающем колонию пространстве, и «глобальной» памятью муравейника, носящей динамический характер.

3.Муравьиные алгоритмы

Муравьиные алгоритмы представляют собой вероятностную жадную эвристику, где вероятности устанавливаются, исходя из информации о качестве решения, полученной из предыдущих решений. Они могут использоваться как для статических, так и для динамических комбинаторных оптимизационных задач. Сходимость гарантирована, то есть в любом случае мы получим оптимальное решение, однако скорость сходимости неизвестна.

3.1. Немного из истории создания муравьиных алгоритмов

Началось всё с изучения поведения реальных муравьёв. Эксперименты с Argentine ants, проводимые Госсом в 1989 и Денеборгом в 1990 году послужили отправной точкой для дальнейшего исследования роевого интеллекта. Исследования применения полученных знаний для дискретной математики начались в начале 90-х годов XX века, автором идеи является Марко Дориго из Университета Брюсселя, Бельгия. Именно он впервые сумел формализовать поведение муравьёв и применить стратегию их поведения для решения задачи о кратчайших путях. Позже при участии Гамбарделлы, Тайлларда и Ди Каро были разработаны и многие другие подходы к решению сложных оптимизационных задач при помощью муравьиных алгоритмов. На сегодняшний день эти методы являются весьма конкурентоспособными по сравнению с другими эвристиками и для некоторых задач дают наилучшие на сегодняшний день результаты.

3.2. Концепция муравьиных алгоритмов

Идея муравьиного алгоритма - моделирование поведения муравьёв, связанного с их способностью быстро находить кратчайший путь от муравейника к источнику пищи и адаптироваться к изменяющимся условиям, находя новый кратчайший путь. При своём движении муравей метит путь феромоном, и эта информация используется другими муравьями для выбора пути. Это элементарное правило поведения и определяет способность муравьёв находить новый путь, если старый оказывается недоступным.

Рассмотрим случай, показанный на рисунке, когда на оптимальном доселе пути возникает преграда. В этом случае необходимо определение нового оптимального пути. Дойдя до преграды, муравьи с равной вероятностью будут обходить её справа и слева. То же самое будет происходить и на обратной стороне преграды. Однако, те муравьи, которые случайно выберут кратчайший путь, будут быстрее его проходить, и за несколько передвижений он будет более обогащён феромоном. Поскольку движение муравьёв определяется концентрацией феромона, то следующие будут предпочитать именно этот путь, продолжая обогащать его феромоном до тех пор, пока этот путь по какой-либо причине не станет недоступен.

Очевидная положительная обратная связь быстро приведёт к тому, что кратчайший путь станет единственным маршрутом движения большинства муравьёв. Моделирование испарения феромона - отрицательной обратной связи - гарантирует нам, что найденное локально оптимальное решение не будет единственным - муравьи будут искать и другие пути. Если мы моделируем процесс такого поведения на некотором графе, рёбра которого представляют собой возможные пути перемещения муравьёв, в течение определённого времени, то наиболее обогащённый феромоном путь по рёбрам этого графа и будет являться решением задачи, полученным с помощью муравьиного алгоритма.

3.3. Обобщённый алгоритм

Любой муравьиный алгоритм, независимо от модификаций, представим в следующем виде •Пока (условия выхода не выполнены)

1. Создаём муравьёв

2. Ищем решения

3. Обновляем феромон

4. Дополнительные действия {опционально}

Теперь рассмотрим каждый шаг в цикле более подробно

1. Создаём муравьёв
   • Стартовая точка, куда помещается муравей, зависит от ограничений, накладываемых условиями задачи. Потому что для каждой задачи способ размещение муравьёв является определяющим. Либо все они помещаются в одну точку, либо в разные с повторениями, либо без повторений.
   • На этом же этапе задаётся начальный уровень феромона. Он инициализируется небольшим положительным числом для того, чтобы на начальном шаге вероятности перехода в следующую вершину не были нулевыми.

2. Ищем решения
   • Вероятность перехода из вершины i в вершину j определяется по следующей формуле

   

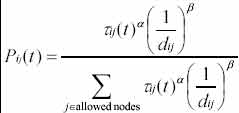
   Где ꚍij

   - уровень феромона, d - эвристическое расстояние, α,β - константные параметры.

3. 
   При α=0 выбор ближайшего города наиболее вероятен, то есть алгоритм становится жадным.
   При β=0 выбор происходит только на основании феромона, что приводит к субоптимальным решениям. Поэтому необходим компромисс между этими величинами, который находится экспериментально.

4. Обновляем феромон
   • Уровень феромона обновляется в соответствии с приведённой формулой
   

   
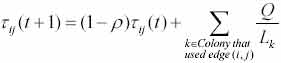
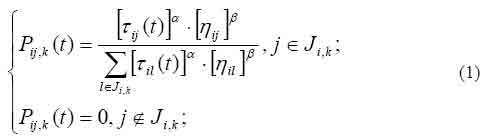   Где ρ - интенсивность испарения, L(t) - цена текущего решения для k-ого муравья, а Q - параметр, имеющий значение порядка цены оптимального решения, то есть - феромон, откладываемый k -ым муравьём, использующим ребро (i,j).

5. Дополнительные действия
   • Обычно здесь используется алгоритм локального поиска, однако он может также появиться и после поиска всех решений.

3.4. Этапы решения задачи при помощи муравьиных алгоритмов

Для того чтобы построить подходящий муравьиный алгоритм для решения какой-либо задачи, нужно

1. Представить задачу в виде набора компонент и переходов или набором неориентированных взвешенных графов, на которых муравьи могут строить решения

2. Определить значение следа феромона

3. Определить эвристику поведения муравья, когда строим решение

4. Если возможно, то реализовать эффективный локальный поиск

5. Выбрать специфический ACO алгоритм и применить для решения задачи

6. Настроить параметр ACO алгоритма

Также определяющими являются

-Количество муравьёв

-Баланс между изучением и использованием

-Сочетание с жадными эвристиками или локальным поиском

-Момент, когда обновляется феромон

4. Применение муравьиных алгоритмов для задачи коммивояжёра

Задача формулируется как задача поиска минимального по стоимости замкнутого маршрута по всем вершинам без повторений на полном взвешенном графе с n вершинами. Содержательно вершины графа являются городами, которые должен посетить коммивояжёр, а веса рёбер отражают расстояния (длины) или стоимости проезда. Эта задача является NP-трудной, и точный переборный алгоритм её решения имеет факториальную сложность.

Моделирование поведения муравьёв связано с распределением феромона на тропе - ребре графа в задаче коммивояжёра. При этом вероятность включения ребра в маршрут отдельного муравья пропорциональна количеству феромона на этом ребре, а количество откладываемого феромона пропорционально длине маршрута. Чем короче маршрут, тем больше феромона будет отложено на его рёбрах, следовательно, большее количество муравьёв будет включать его в синтез собственных маршрутов. Моделирование такого подхода, использующего только положительную обратную связь, приводит к преждевременной сходимости - большинство муравьёв двигается по локально оптимальному маршруту. Избежать этого можно, моделируя отрицательную обратную связь в виде испарения феромона. При этом если феромон испаряется быстро, то это приводит к потере памяти колонии и забыванию хороших решений, с другой стороны, большое время испарения может привести к получению устойчивого локального оптимального решения.

Теперь с учётом особенностей задачи коммивояжёра, мы можем описать локальные правила поведения муравьёв при выборе пути.

1. Муравьи имеют собственную "память". Поскольку каждый город может быть посещён только один раз, то у каждого муравья есть список уже посещённых городов - список запретов. Обозначим через J_ik список городов, которые необходимо посетить муравью k, находящемуся в городе i.

2. Муравьи обладают "зрением" - видимость есть эвристическое желание посетить город j, если муравей находится в городе i. Будем считать, что видимость обратно пропорциональна расстоянию между городами η_ij=1/D_ij.

3. Муравьи обладают "обонянием" - они могут улавливать след феромона, подтверждающий желание посетить город j из города i на основании опыта других муравьёв. Количество феромона на ребре (i,j) в момент времени t обозначим через τ_ij(t) .

4. На этом основании мы можем сформулировать вероятностно-пропорциональное правило, определяющее вероятность перехода k-ого муравья из города i в город j:
   

   
   Где α,β - параметры, задающие веса следа феромона. При α=0 алгоритм вырождается до жадного алгоритма (будет выбран ближайший город). Заметим, что выбор города является вероятностным, правило (1) лишь определяет ширину зоны города j; в общую зону всех городов J_ik бросается случайное число, которое и определяет выбор муравья. Правило (1) не изменяется в ходе алгоритма, но у двух разных муравьёв значение вероятности перехода будут отличаться, т.к. они имеют разный список разрешённых городов.

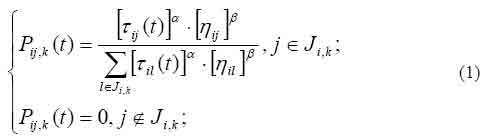
5. Пройдя ребро (i,j), муравей откладывает на нём некоторое количество феромона, которое должно быть связано с оптимальностью сделанного выбора. Пусть T_k(t) есть маршрут, пройденный муравьём k к моменту времени t, L_k(t) - длина этого маршрута, а Q - параметр, имеющий значение порядка длины оптимального пути. Тогда откладываемое количество феромона может быть задано в виде
   

   
   Правила внешней среды определяют, в первую очередь, испарение феромона. Пусть p=[0,1] есть коэффициент испарения, тогда правило испарения имеет вид
   
   где m - количество муравьёв в колонии.

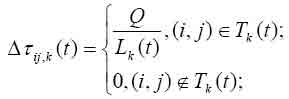
В начале алгоритма количества феромона на рёбрах принимается равным небольшому положительному числу. Общее количество муравьёв остаётся постоянным и равным количеству городов, каждый муравей начинает маршрут из своего города.

Дополнительная модификация алгоритма может состоять в ведении так называемых "элитных" муравьёв, которые усиливают рёбра наилучшего маршрута, найденного с начала работы алгоритма. Обозначим через T* наилучший текущий маршрут, через L* - его длину. Тогда если в колонии есть e элитных муравьёв, то рёбра маршрута получат дополнительное количество феромона

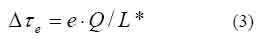
4.1. Муравьиный алгоритм для задачи коммивояжёра в псевдокоде

1. Ввод матрицы расстояний D

2. Инициализация параметров алгоритма - α,β,e,Q

3. Инициализация рёбер - присвоение видимости η_ij и начальной концентрации феромона

4. Размещение муравьёв в случайно выбранные города без совпадений

5. Выбор начального кратчайшего маршрута и определение L* //Основной цикл

6. Цикл по времени жизни колонии t=1,t_max

7. Цикл по всем муравьям k=1,m

8. Построить маршрут T_k(t) по правилу (1) и рассчитать длину L_k(t)

9. конец цикла по муравьям

10. Проверка всех L_k(t) на лучшее решение по сравнению с L*

11. В случае если решение лучше, обновить L* и T*

12. Цикл по всем рёбрам графа

13. Обновить следы феромона на ребре по правилам (2) и (3)

14. конец цикла по рёбрам

15. конец цикла по времени

16. Вывести кратчайший маршрут T* и его длину L*

Сложность данного алгоритма, как несложно заметить, зависит от времени жизни колонии (t_max) городов (n) и количества муравьёв в колонии (m).

5. Области применения и возможные модификации

Поскольку в основе муравьиного алгоритма лежит моделирование передвижения муравьёв по некоторым путям, то такой подход может стать эффективным способом поиска рациональных решений для задач оптимизации, допускающих графовую интерпретацию. Ряд экспериментов показывает, что эффективность муравьиных алгоритмов растёт с ростом размерности решаемых задач оптимизации. Хорошие результаты получаются для нестационарных систем с изменяемыми во времени параметрами, например, для расчётов телекоммуникационных и компьютерных сетей. В Интернете можно найти описание применения муравьиного алгоритма для разработки оптимальной структуры съёмочных сетей GPS в рамках создания высокоточных геодезических и съёмочных технологий. В настоящее время на основе применения муравьиных алгоритмов получены хорошие результаты для таких сложных оптимизационных задач, как задача коммивояжёра, транспортная задача, задача календарного планирования, задача раскраски графа, квадратичная задача о назначениях, задача оптимизации сетевых трафиков и ряд других.

Качество получаемых решений во многом зависит от настроечных параметров в вероятностно- пропорциональном правиле выбора пути на основе текущего количества феромона и от параметров правил откладывания и испарения феромона. Возможно, что динамическая адаптационная настройка этих параметров может способствовать получению лучших решений. Немаловажную роль играет и начальное распределение феромона, а также выбор условно оптимального решения на шаге инициализации.

Перспективными путями улучшения муравьиных алгоритмов являются различные адаптации параметров с использованием базы нечётких правил и их гибридизация, например, с генетическими алгоритмами. Как вариант, такая гибридизация может состоять в обмене через определённые промежутки времени текущими наилучшими решениями.

6. Достоинства и недостатки муравьиных алгоритмов

6.1. Достоинства:

 Для TSP (Traveling Salesman Problem) сравнительно эффективны
o Для небольшого количества узлов TSP может быть решена полным перебором
o Для большого количества узлов TSP вычислительно сложна (NP-трудная) - экспоненциальное время сходимости

 Работают лучше, чем другие глобальные оптимизации для TSP (нейронные сети, генетические алгоритмы)

 Сравнение с GAs (Genetic Algorithms):
o Опираются на память обо всей колонии вместо памяти только о предыдущем поколении
o Меньше подвержены неоптимальным начальным решениям (из-за случайного выбора пути и памяти колонии)

 Могут использоваться в динамических приложениях (адаптируются к изменениям, скажем, расстояний)

 Применялись к множеству различных задач
o Routing
o TSP (Traveling Salesman Problem)
o Vehicle Routing
o Sequential Ordering
o Machine Learning
o Classification Rules
o Bayesian networks
o Fuzzy systems
o Network Routing
o Connection oriented network routing
o Connection network routing
o Optical network routing
o Scheduling
o Job Shop
o Open Shop
o Flow Shop
o Total tardiness (weighted/non- weighted)
o Project Scheduling
o Group Shop
o Subset
o Multi-Knapsack
o Max Independent Set
o Redundancy Allocation
o Set Covering
o Weight Constrained Graph Tree partition
o Arc-weighted L cardinality tree
o Maximum Clique
o Assignment
o QAP (Quadratic Assignment Problem)
o Graph Coloring
o Generalized Assignment
o Frequency Assignment
o University Course Time Scheduling
o Other
o Shortest Common Sequence
o Constraint Satisfaction
o 2D-HP protein folding
o Bin Packing

6.2. Недостатки:

 Теоретический анализ затруднён: o В результате последовательности случайных (не независимых) решений
o Распределение вероятностей меняется при итерациях
o Исследование больше экспериментальное, нежели теоретическое

 Сходимость гарантируется, но время сходимости не определено

 Обычно необходимо применение дополнительных методов таких, как локальный поиск

 Сильно зависят от настроечных параметров, которые подбираются только исходя из экспериментов

7. Источники

1. Штовба С.Д. Муравьиные алгоритмы // Exponenta Pro. Математика в приложениях, 2003, №4, с.70-75.

2. МакКоннелл Дж. Основы современных алгоритмов. - М.: Техносфера, 2004. - 368 с.

3. Thompson, Jonathan. Ant Colony Optimization. //

4. www.orsoc.org.uk/region/regional/swords/swords.ppt

5. Barker T. and Von Haartman M. Ant Colony Optimization. //

6. courses.washington.edu/inde510/510/Ant Colony Optimization3.ppt

7. www.cosc.brocku.ca/Offerings/3P71/Lectures/ACO.ppt