ОБ ОДНОМ «МУРАВЬИНОМ» АЛГОРИТМЕ
А.А. Кажаров, В.М.Курейчик
Источник: www.raai.org/cai-08/files/cai-08_paper_144.doc
В этой работе рассматривается решение классической NP-трудной задачи о коммивояжере на основе муравьиных алгоритмов. Данная задача без каких-либо изменений в ее интерпретации решается для проектирования СБИС. В основе идеи этого алгоритма лежит моделирование поведения муравьев. Колония представляет собой систему с очень простыми правилами автономного поведения особей. Несмотря на примитивность поведения каждого муравья, поведение всей колонии оказывается достаточно разумным. Предложены и исследованы различные модификации. В ходе проделанной работы была разработан алгоритм, реализующий описанную модель поведения муравьев с модификациями. Экспериментальные исследования доказали эффективность муравьиных алгоритмов с модификациями по сравнению со стандартными муравьиным и генетическим алгоритмами.
Введение
В этой работе рассматривалось решение классической NP-трудной задачи о коммивояжере на основе муравьиных алгоритмов (МА). Данный класс алгоритмов разрабатывался в рамках научного направления, которое можно назвать «природные вычисления» [1]. Исследования в этой области начались в середине 90-х годов XX века, автором идеи является Марко Дориго из Университета Брюсселя, Бельгия [2, 3, 4]. В основе этой идеи лежит моделирование поведения колонии муравьев. В ходе проделанной работы были реализованы и исследованы предложенные модификации МА. На различных бенчмарках для задачи о коммивояжере получены маршруты, лучшие известных.
1. Постановка задачи коммивояжера
Как известно, задача о коммивояжере относится к NP-трудным. Она заключается в нахождении кратчайшего гамильтонова цикла в графе. Без каких-либо изменений в постановке она используется для проектирования СБИС.
Более строго постановка задачи звучит следующим образом: дан граф G=(X,U), где |X| = n – множество вершин (города), |U| = m – множество ребер. Дана матрица чисел D(i, j), где 1 ? i, j ? n, представляющих собой стоимость ребра между вершинами xi, xj. Требуется найти перестановку ? из элементов множества X, такую, что значение целевая функция (ЦФ) равно:
2. Муравьиный алгоритм
2.1. Общие положения
Как было сказано выше, основная идея данного алгоритма является моделирование поведения муравьев, коллективной адаптации. Колония представляет собой систему с очень простыми правилами автономного поведения особей. Однако, несмотря на примитивность поведения каждого отдельного муравья, поведение всей колонии оказывается достаточно разумным [5]. Таким образом, основой поведения муравьиной колонии служит низкоуровневое взаимодействие, благодаря которому, в целом, колония представляет собой разумную многоагентную систему. Взаимодействие определяется через химическое вещество – феромона, откладываемого муравьями на пройденном пути. При выборе направления движения муравей исходит не только из желания пройти кратчайший путь, но и из опыта других муравьев, информацию о котором получаем через уровень феромонов ребрах. С течением времени происходит процесс испарения феромонов, которое является отрицательной обратной связью.
2.2. Свойства муравья
1. Каждый муравей обладает собственной «памятью», в котором будет храниться список городов Ji,k, которые необходимо посетить муравью k, который находится в городе i.
2. Муравьи обладают «зрением», обратно пропорциональный длине ребра:
?ij = 1/Dij.
3. Каждый муравей способен улавливать след феромона, которое будет определять желание муравья пройти по данному ребру. Уровень феромона в момент времени t на ребре Dij будет соответствовать ?ij(t).
4. Вероятность перехода муравья из вершины i в вершину j будет определяться следующим соотношением:
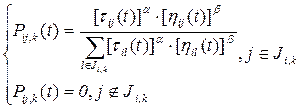 , (1)
, (1)
где ?, ? – эмпирические коэффициенты [6]. Нетрудно заметить, что данное выражение имеет эффект «колеса рулетки». Количество откладываемого феромона:
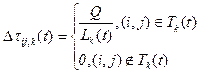 , (2)
, (2)
где Q – параметр, имеющий значение порядка длины оптимального пути, Lk(t) – длина маршрута Tk(t). Испарение феромона определяется следующим выражением:
![]() , (3)
, (3)
где m – количество муравьев, p – коэффициент испарения (0 ? p ? 1).
3. Модификации МА
3.1. «Элитные» муравьи
Элитой называются муравьи, чьи маршруты лучше остальных. Разработана следующая модификация, основанная на знаниях об «элитных» муравьях. Данная модификация не учитывает количества элитных муравьев. Выражение (2) для элиты принимает вид:
![]() , (4)
, (4)
где Ae – «авторитет» элитных муравьев. Таким образом, мы можем регулировать влияние «элитных» муравьев с помощью коэффициента Ae. Оптимальное значение Ae, в основном, будет зависеть от размерности графа, численности колонии, времени жизни. Его значение во многом определяет скорость сходимости. Это очень важно, поскольку в реальных ситуациях чаще всего приходится балансировать между качеством решения и временем работы.
3.2. Начальное расположение колонии
В простом МА принято считать, что в каждой вершине изначально находится по одному муравью. В данной работе представлены следующие стратегии начального расположения:
1. «Одеяло» – реализация стандартного размещения муравьев, в каждой вершине находиться по одному муравью. Тогда сложность данного алгоритма выражается следующей зависимостью – O(t*n3), поскольку n=m;
2. «Дробовик» – случайное распределение муравьев на вершины графа, причем необязательно, чтобы численности колонии и вершин совпадали;
3. «Фокусировка» – вся колония находится в одной вершине;
4. «Блуждающая колония» – в каждый момент времени, т.е. на каждой итерации, вся колония перемещается в случайно выбранную вершину.
Отметим, что названия первых трех заимствованы из названий стратегий формирования начальной популяции в генетических алгоритмах (ГА), также относящихся к классу алгоритмов «природных вычислений» [7]. В ходе проделанных экспериментальных исследований было выяснено, что сходимость МА и качество решения сильно зависят от начального расположения колонии.
3.3. Шаблоны
Технология выделения шаблонов давно применяется в ГА. Шаблонами, иначе схемами, называются фрагменты решений. В ГА шаблоны формируются согласно форме представления структуры хромосомы. Например, ***1*110* или 0***0***** – схемы, где * означает, что на этой позиции может находиться любой элемент [7].
В данной работе исследовалась возможность применения шаблонов в МА. В отличие от ГА здесь мы будем рассматривать лишь одну единственную схему для маршрутов всех муравьев. Актуальность формирования схемы объясняется большими временными затратами на сложные математические вычисления при нахождении вероятностей перехода из одной вершины в другие как видно из (1). Сложность алгоритма нахождения следующей вершины – O(n*k), где n – число вершин, а k – некоторый коэффициент больший 1. Это объясняется, как было указано выше, такими сложными математическими операциями, как возведение вещественного числа в степень. Имея же шаблон, мы получаем следующую вершину за O(1).
Кодировка шаблона следующая. Пусть имеется вектор B размерностью n, где n – число вершин в графе. Тогда Bi будет содержать номер вершины, в которую необходимо перейти из вершины i. Таким образом, исследуемый шаблон представляет собой набор «строительных» блоков [7]. Рассмотрим следующий пример:
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Bi |
7 |
6 |
* |
* |
* |
3 |
* |
На основе B мы можем составить следующие «строительные» блоки: (1-7), (2-6-3). Таким образом, попадая в вершину 2, муравей без лишних предвычислений переходит в вершину 6, а затем в 3. Из 7, соответственно, в 1.
Разработаны следующие стратегии формирования шаблона:
1. Статический шаблон – формирование шаблона перед началом работы МА на основе знаний о длинах ребер. Пусть заранее задано число фиксированных ребер: 1?Es?n, где n – число вершин. Тогда шаблон заполняем информацией об Es ребрах минимальной длины. При Es = n сводится к алгоритму «ближайшего соседа».
2. Динамический шаблон – формирование шаблона по ходу работы МА. Шаблон заполняется информацией о Es ребрах, на которых отложено наибольшее количество феромонов.
3.4. Выпрямление
Данная модификация связана с использованием частичного перебора в полученном решении. Для этого случайно выбирается часть решения, который будет являться маршрутом заданной длины l (количество вершин). Рассмотрим на следующем примере.
|
Позиции |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Вершины |
1 |
6 |
9 |
3 |
7 |
8 |
4 |
2 |
10 |
5 |
1 |
Пусть l = 5, а выбранный маршрут представляется как часть решения с 4 позиции по 8:
|
3 |
7 |
8 |
4 |
2 |
Далее, используя алгоритм перебора на основе метода «ветвей и границ» [8], получаем кратчайший маршрут на заданном множестве вершин. Таким образом, возникает эффект «выпрямления» на участке решения. Конечное решение представляет собой маршрут:
|
Позиции |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Вершины |
1 |
6 |
9 |
3 |
8 |
4 |
7 |
2 |
10 |
5 |
1 |
В МА «выпрямление» выступает в качестве интеллектуального блока (назовем его «выпрямитель») или черного ящика, на входе которого подается подграф с исходным множеством вершин и отношениями между ними (весами ребер), а на выходе получаем кратчайший обход этих вершин. На рис. 1 отображен рассмотренный выше пример. Жирными линиями выделены ребра, входящие в подграф («область выпрямления»).
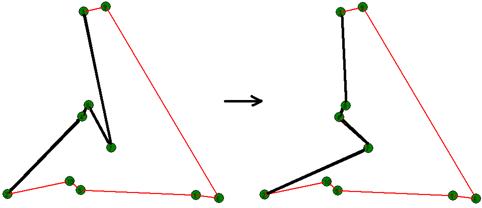
а) до выпрямления б) после выпрямления
Рис. 1. Пример использования выпрямления
Определим влияние «выпрямителей» на ВСА всего алгоритма. Псевдокод модифицированного МА имеет следующий вид:
1. Ввод матрицы расстояний D
2. Инициализация параметров алгоритма - ?, ?, Q, Ae, l
3. Инициализация ребер – присвоение видимости ?ij и начальной концентрации феромона
4. Модифицированная стратегия начального размещения муравьев
5. Выбор начального кратчайшего маршрута T* и определение L*
6. Цикл по времени жизни колонии t=1,tmax
7. Цикл по всем муравьям k=1,m
8. Построить маршрут T на основе (1) и шаблона и рассчитать длину L
9. Промежуточное выпрямление T и пересчет L
10. Если L < L*, то L*=L и T*=T
11. конец цикла по муравьям
12. Цикл по всем ребрам графа
13. Обновить следы феромона на ребре на основе (3)
14. конец цикла по ребрам
15. Формирование шаблона
16. Обновить следы феромона «элиты» на основе (4)
17. конец цикла по времени
18. Дополнительное выпрямление T* и пересчет L*
19. Вывести кратчайший маршрут T* и его длину L*
Отсюда видно, что ВСА как O(t*(m*(n2+l!)) или O(t*m*n2+ t*m*l!). Тогда ВСА модифицированного МА будет выше стандартного в K раз, где
![]() . (5)
. (5)
Т.е. при n=100, l=8-9 ВСА согласно (5) увеличится в среднем лишь в 2 раза. Выражение (5) является верхней оценкой относительного увеличения ВСА, так как используется не полный перебор, а перебор на основе метода «ветвей и границ». Таким образом, использование частичного перебора в не требует больших временных затрат, но значительно улучшает решения муравьев, получаемые на начальной стадии адаптации. Выражение (5) подтверждено экспериментальными исследованиями. Выделены два вида «выпрямления»: промежуточное и дополнительное. Промежуточное «выпрямление» подробно рассмотрено выше. Он применяется к промежуточным решениям, получаемыми муравьями в течение времени жизни колонии. Дополнительное «выпрямление» применяется после окончания времени жизни колонии и применяется лишь к лучшему решению T*. Однако, в отличие от промежуточного «выпрямления» здесь «выпрямитель» применяется неоднократно к разным участкам маршрута. Выбор участков маршрута может быть как произвольным, так и выборочным на основе какого-то алгоритма или закономерности. В данной работе предлагается выбирать участки решения, начиная с первой позиции до n-l с шагом l/2. Для предыдущего примера такими участками будут:
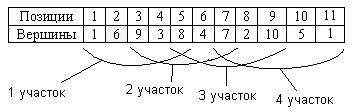
Рис.2. Выбор участков маршрута для дополнительного «выпрямления»
Для дополнительного «выпрямителя» можно индивидуально выбирать значение l* – длины участка перебора. А значит, имеет смысл применять несколько видов «выпрямителей».
4. Экспериментальные исследования
Для проведения исследований была создана программа в интегральной среде разработки Borland C++ Builder 6.0. Экспериментальные исследования проводились со стандартными бенчмарками – графы с 30, 50, 75 и 98 вершинами. Все рассматриваемые графы полносвязные, поэтому задаются только координаты вершин, а веса ребер определяются как декартово расстояние между вершинами:
![]() .
.
На рис. 3 показан графический интерфейс отображения процесса работы алгоритма.
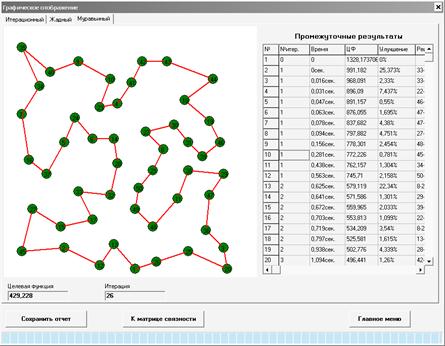
Рис. 3. Отображение процесса работы алгоритма
Результаты сравнивались с известными наилучшими решениями, которые были получены с использованием модифицированного генетического алгоритма[9]. Приведем сравнения полученных решений на некоторых бенчмарках. Слева показаны существующие результаты, справа – полученные.
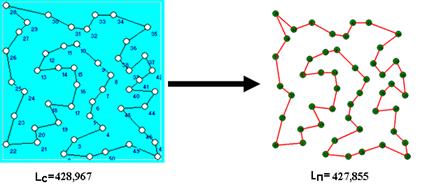
Рис. 4. Бенчмарка с 50 вершинами

Рис. 5. Бенчмарка с 75 вершинами
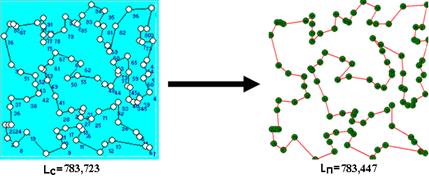
Рис. 6. Бенчмарка с 98 вершинами
5. Заключение
В ходе проделанной работы была разработан алгоритм, реализующий описанную модель поведения муравьев. Полученные результаты позволяют судить об оптимальном выборе параметров при решении задачи о коммивояжере с различными начальными данными. Преимущество модифицированного МА перед ГА и стандартным МА при решении этой задачи подтверждено экспериментальными исследованиями.
Литература
1. Штовба С.Д. Муравьиные алгоритмы. 2003г.
2. Bonavear F., Dorigo M. Swarm Intelligence: from Natural to Artificial Systems. Oxford university Press. 1999.
3. Corne D., Dorigo M., Glover F. New Ideas in Optimization. McGrav-Hill. 1999.
4. http://iridia.ulb.ac.be/dorigo/ACO/ACO.html.
5. МакКоннелл Дж. Основы современных алгоритмов. – М.: Техносфера, 2004г.
6. Кирсанов М. Н. Графы в Maple.Задачи, алгоритмы, программы. – М: ФИЗМАТЛИТ, 2007г.
7. Гладков Л.А., Курейчик В.М., Курейчик В.В. Генетические алгоритмы. – Ростов-на-Дону: ООО «Ростиздат», 2004г.
8. Гладков Л.А., Курейчик В.М., Курейчик В.В. Основы теории алгоритмов: Учебное пособие по курсу «Математическая логика и теория алгоритмов». – Таганрог: изд-во ТРТУ, 2002г.
9. Victor M. Kureichick, Victor V. Miagkikh, Alexander P. Topchy. Genetic Algorithm for Solution of the Traveling Salesman Problem with New Features against Premature Convergence.