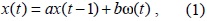
Источник информации: http://www.nbuv.gov.ua/portal/natural/ovp/2008_2009/opt_10/opt10-08.pdf
Фильтрация временных рядов остается одним из актуальных приложений теории управления.
Анализ связанных с этим направлением многочисленных публикаций показывает, что к настоящему
времени существует большое число методов фильтрации, в том числе адаптивных, отличающихся
типами оцениваемых сигналов, присутствующих помех, прогнозирующих или настраиваемых моделей,
критериями и алгоритмами оценивания [1]. Однако во многих случаях получаемые оценки расходятся с
действительными значениями элементов оцениваемых рядов, особенно в условиях априорной
неопределенности о вероятностных распределениях возмущений. Поэтому проблема создания просто
реализуемых адаптивных фильтров с удовлетворительной сходимостью к действительным значениям
оцениваемых величин по-прежнему актуальна.
Целью статьи является адаптивная фильтрация временных рядов в виде результатов текущих
наблюдений за местоположением морского дрифтера, моделируемых в виде динамической системы
первого порядка.
В рассматриваемом случае динамика отклонений реальных значений координат (широты и
долготы в градусах) морского дрифтера от средних значений (рисунок 1), как показал предварительный
анализ данных, описывается уравнением авторегрессии первого порядка
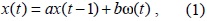
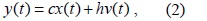
 конечны, но их значения неизвестны.
конечны, но их значения неизвестны.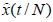 . Первый индекс указывает на момент оценивания,
второй – на количество используемых наблюдений. При N = t используем упрощенное обозначение
. Первый индекс указывает на момент оценивания,
второй – на количество используемых наблюдений. При N = t используем упрощенное обозначение 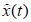 вместо
вместо 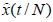 .
.

При известных характеристиках шумов оценка состояния системы (1), (2) в момент t+1 по
наблюдениям y(t),...,y(1), минимизирующая квадратичный критерий, задается рекуррентными
соотношениями, составляющими оптимальный алгоритм оценивания (фильтр Калмана).
При неизвестных (частично или полностью) ковариационных функциях сообщения или шумов,
как в рассматриваемом случае, фильтр Калмана становится неработоспособным. В этих условиях для
оценивания координат местоположения дрифтера можно воспользоваться методами адаптивной
фильтрации. В отличие от традиционных фильтров адаптивные фильтры предполагают обратную связь.
Входной сигнал фильтруется или взвешивается для получения сигнала, который затем сравнивается с
полезным, стандартным или обучающим сигналом для определения ошибки. Ошибка, в свою очередь,
используется для корректировки весовых коэффициентов фильтра с целью постепенной минимизации
ошибки. Другими словами, параметры фильтра подстраиваются таким образом, чтобы обеспечить
близкое к оптимальному качество оценивания.
Для оценки состояния системы (1),(2) применим схему адаптивной фильтрации [2], предполагая,
что x(t) характеризуется плотностью вероятности g(t), а искомая оценка 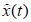 – плотностью вероятности
f(x;y) . Информационное расхождение Кульбака между неизвестной плотностью вероятности и его
оценкой определяется соотношением [3]
– плотностью вероятности
f(x;y) . Информационное расхождение Кульбака между неизвестной плотностью вероятности и его
оценкой определяется соотношением [3]
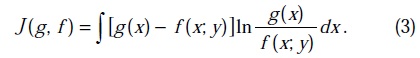

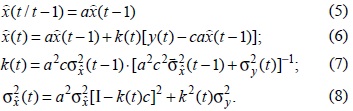
Здесь через  обозначена априорная оценка x(t), через
обозначена априорная оценка x(t), через 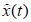 – апостериорная в отличие от
оптимальных оценок
– апостериорная в отличие от
оптимальных оценок 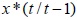 и
и 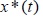 , получаемых с использованием фильтра Калмана. В уравнения
(7), (8) вместо неизвестных дисперсий шумов
, получаемых с использованием фильтра Калмана. В уравнения
(7), (8) вместо неизвестных дисперсий шумов 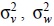 входят дисперсия
входят дисперсия  оценки состояния
оценки состояния 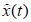 и дисперсия
и дисперсия  наблюдаемой случайной последовательности y(t).
наблюдаемой случайной последовательности y(t).
Подстановка в выражения (7), (8) выборочных дисперсий 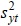 и
и 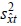 вместо дисперсий
вместо дисперсий  и
и  ,
соответственно, позволяет найти выражения для коэффициента усиления фильтра
,
соответственно, позволяет найти выражения для коэффициента усиления фильтра

и дисперсии оценки

Фильтр для системы (1),(2), описываемый выражениями (5), (6) и (9), (10) реализован с
использованием прикладного программного обеспечения RATS (ESTIMA) [5].
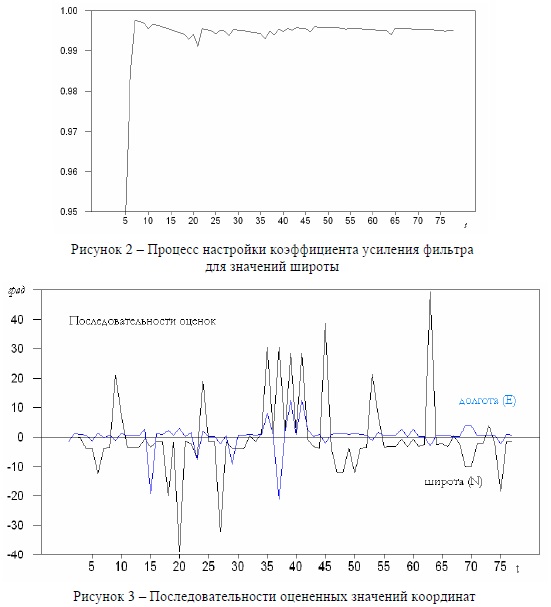
Для анализируемой системы коэффициент усиления адаптивного фильтра k(t) настраивается
достаточно быстро и приблизительно с 10 измерения устанавливается на уровне 0,9379 (рисунок 2) (для
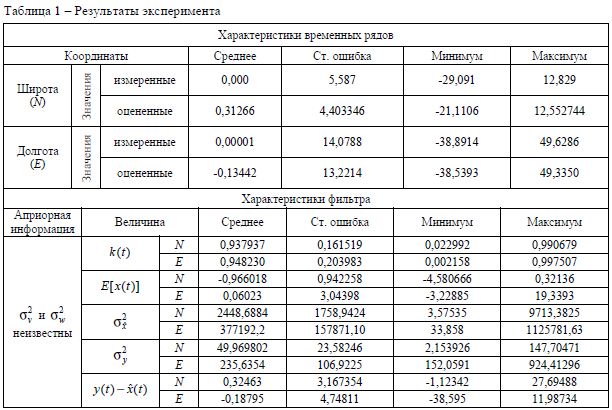
широты) и на уровне 0,996 (для долготы). На графиках, изображенных на рисунке 3, представлена
последовательность оцененных значений координат, на рисунке 4 – последовательности ошибок
оценивания. Анализ ошибок оценивания показал, что они статистически независимы и распределены по
нормальному закону с нулевым средним. Результаты экспериментальных исследований приведены в
таблице 1.

Сформированный алгоритм позволяет решать задачу фильтрации в темпе поступления измерений
по каналу космической связи. Результаты эксперимента демонстрируют его быструю сходимость к
действительным значениям оцениваемых величин.
Будущие исследования могут быть связаны с оцениванием случайных последовательностей с
малым значением дисперсии и разработкой программного обеспечения для исследования многомерных
систем большой размерности.
Библиографический список
1. Балакришнан А.В. Теория фильтрации Калмана / А.В. Балакришнан. — М.: Мир, 1988. — 168 с.
2. Первухина Е.Л. Использование информационной меры в процедурах оценки дискретных
стохастических систем при неизвестных ковариациях шумов / Е.Л. Первухина // Известия РАЕН. Сер.
Математика, математическое моделирование, информатика и управление. — 1999. — Т. 3. — № 3. —
С. 100–106.
3. Кульбак С. Теория информации и статистика / С. Кульбак. — М.: Наука, 1967. — 408 c.
4. Pervukhina E. Adaptive time series filters obtained by minimization of the Kullback-Leibler
divergence criterion / E. Pervukhina, J.-F. Emmenegger // International Journal of Applied Mathematics. —
2005. — V. 17. — N 1. — P. 69–89.
5. Doan T.A. RATS Software Package, User’s Manual, Version 6.0. / T.A. Doan. — Illinois: ESTIMA,
2005. — 364 p.