Цифровая фильтрация временных рядов

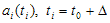
Источник информации: http://www.financenature.com/articles/14-data-processing/11-digital-filtration.html

    Принятые сокращения
    КУ - коэффициент усиления
    ПФ - передаточная функция
    ДВР - дискретный временной ряд
    ЦФ - цифровой фильтр

    Определение проблемы
    Временной ряд - это упорядоченная по времени последовательность одной или нескольких переменных. Временной ряд может описываться непрерывным или дискретным образом.

    Все процессы, протекающие в природе, непрерывны. Трудно себе представить, чтобы, к примеру, погода менялась скачкообразно. Для того, чтобы записать непрерывный временной ряд, необходимо выбрать достаточный период дискретизации - равные промежутки времени, через которые замеряются показатели временного ряда. При этом временной ряд может быть представлен в виде ряда членов a₀, a₁, ..., a_N:

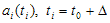
     здесь:

     Δ - период дискретизации, t₀ - время начала измерений ряда;

    В каждой конкретной задаче требуется выбрать одновременно необходимый достаточный период дискретизации данных. Слишком малый период приведет к избыточному количеству данных, слишком крупный - к потере информации.

    Реальные временные ряды всегда содержат в себе полезную информацию и шум. Шумом назовем некоторую составляющую каждого члена временного ряда, не несущую информационной нагрузки. В контексте прогноза погоды шумом можно назвать незначительные колебания температуры вокруг устойчивого среднего значения, вызванные окружающей средой.

    Самый наглядный пример шума - аналоговая радиопередача или телепередача. Из-за множества природных и техногенных факторов сигнал с радио- или телестанции (осмысленная передача) смешивается с шумом, который представляет одну лишь помеху для зрителя. Если шума в радиосигнале больше, чем передачи - слова диктора становится невозможно разобрать, или они вообще тонут за стеной треска. Однако, если шума немного - слова можно разобрать совершенно точно.

    В данной статье как пример финансового временного ряда я буду рассматривать курсы валютной пары EUR/USD на рынке Forex.

    Качественное отличие потока котировок от радиопередачи - невозможность напрямую отличить полезный сигнал от шума (детерминировать шум). Можно лишь сделать некоторые допущения о природе и значении шума, на которые в дальнейшем и опираться.

    Таким образом, важной целью цифровой фильтрации временных рядов является детерминирование предполагаемого уровня шума. Исходя из найденного уровня, становится возможным делать дальнейшие выводы и предположения о характере некоторого периода временного ряда (например, используя биржевые термины, делать предположение о факте тренда или бокового движения).  Перейдем теперь к конкретной теории.

    Цифровым фильтром называется фильтр, принимающий на входе цифровой (дискретный) сигнал и усиливающийего согласно частотной характеристике. Не углубляясь в теорию фильтров, приведу несколько фактов, позволяющих лучше понять принцип действия такого фильтра.

    1) фильтр призван ослаблять определенный диапазон частот сигналов

    Слово "фильтрация" в данном случае означает "ослабление". Частотная характеристика фильтра определяет, насколько и какие именно частоты он ослабляет. Вариант частотной функции фильтра высоких частот представлен на следующем рисунке:

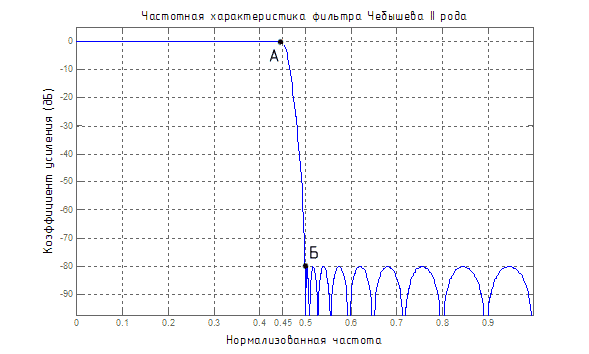
    Из графика видно, что до 0,45 нормализованной частоты (точка А) сигнал не усиливается (остается на прежнем уровне), а к уровню частоты 0,5 (точка Б) его ослабление составляет -80 дБ, то есть 10⁴ раз (20 дБ соответствуют усилению в 10¹ раз, -20 дБ - ослаблению в 10¹ раз). Колебания коэффициента усиления после уровня частоты 0,5 в данном случае значения не имеют из-за своей малости (менее 0,0001 от исходного сигнала).

     2) диапазон обрабатываемых фильтром частот ограничен

    Фильтр способен обрабатывать составляющие сигнала с частотой не выше половины частоты дискретизации (доказательство этого факта следует из теоремы Котельникова). На практике следует ужесточать это ограничение в полтора-два раза.

    На этом месте я считаю нужным напомнить практический смысл фильтра при работе с временным рядом цен. Фильтрация высокочастотной составляющей позволяет исключить из расчета постоянные и незначительные колебания цены - а ведь это и есть пресловутый шум!

    Предположим, мы хотим проанализировать движение цены за неделю с периодом дискретизации 1 минута, и притом не брать во внимание мелкие внутридневные колебания. Похоже, с этой задачей превосходно справится фильтр высоких частот, настроенный на ослабление частот выше внутридневных колебаний (например, колебаний с периодом 30 минут и меньше). В этом случае частота ослабления должна составить 1/(30*60) = 1/1800 Гц.

    При торговле для сглаживания линии цены чаще всего используется метод скользящей средней N-го периода. При этом текущее значение сигнала после фильтрации равно усредненному значению цен в N предшествующих точках временного ряда (v[-1], v[-2], ..., v[-N]). Скользящая средняя не создает при своем расчете абсолютно никаких сложностей, но и, однако, не несет в своем обозначении конкретной информации о фильтруемых частотах.

    Функция скользящей средней линии M-го порядка может быть записана в виде простейшего разностного уравнения:

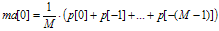
     Это разностное уравнение соответствует следующей передаточной функции:

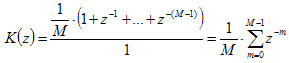
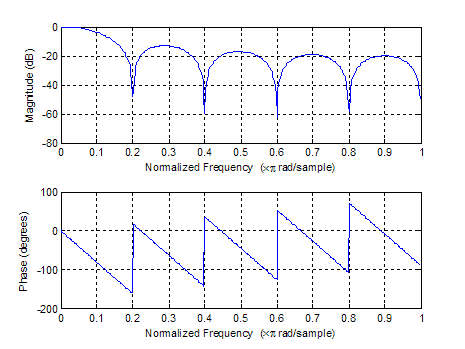
    При нулевой частоте колебаний (постоянный сигнал) КУ равен единице (0 дБ).

    При стремлении частоты колебаний к единице (период колебания - одна дискрета, то есть частота колебаний максимальна) КУ имеет пики усиления, стремящиеся к 0,1 (-20 дБ) и минимумы усиления, стремящиеся к 0,001 (-60 дБ).

    Очевидной, рабочей частотой такого фильтра следует считать частоту, на которой происходит ослабление сигнала на 3 дБ (в 1,4 раза). MA10 соответствует нормализованной частоте ~0,088 Гц, или ~11,25 дискрет. Таким образом, граничный фильтруемый период колебаний составляет 11 периодов дискретизации. При этом десятикратное ослабление применяется уже к колебаниям с периодом менее 5,5 дискрет.

    Ниже приведена зависимость граничной частоты фильтрации в зависимости от периода средней скользящей:

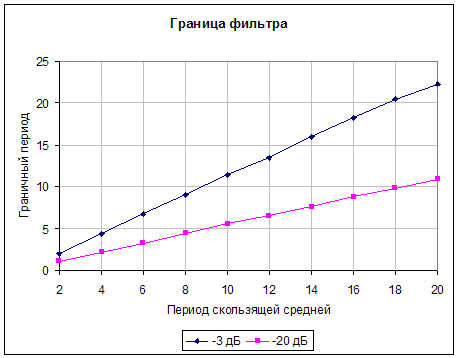
    Функции границы по уровням ослабления -3 дБ и -20 дБ прямолинейны и имеют вид:

 

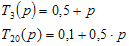
    Я уверен, что Вы уже догадались, зачем это все нужно. Исследователь должен представлять себе, как именно он обрабатывает данные - и какую их часть он намеренно теряет. Замечу, что мы считаем использование фильтров для торговли отличным признаком непрофессионализма. Фильтры предназначены для первичной обработки данных и детерминирования составляющих сигнала; попытки делать что-то большее подобны стрельбе вслепую.

    Итак, весь вопрос в осмысленном использовании настраиваемого фильтра (например, фильтра Чебышева). Сравните первый и второй рисунки - там отчетливо видны четыре ключевые особенности настраиваемого фильтра:

    1) коэффициент усиления до границы фильтрации равен единице, то есть фильтрующие свойства не проявляются

    2) диапазон частот между точками А и Б может быть весьма малым

    3) максимум коэффициента усиления в зоне фильтрации может быть настроен практически на нулевой уровень

    4) уровень пульсаций в зоне фильтрации может быть ничтожно мал

    С точки зрения программирования, реализация ЦФ предельно проста. Сообразно синтезированной передаточной функции фильтра (удобным Вам способом) строится разностное уравнение, которое представляет собой функцию нескольких переменных.

    Каждый раз, работая со скользящим средним, люди неосознанно работают с цифровым фильтром - но осуществляют эмпирический подбор коэффициентов фильтра, а не его настройку. И кто же кем управляет в таком случае? Перефразируя известную фразу, "или вы управляете фильтрами, или фильтры управляют вами".

    Итак, подошло время демонстрации./p>

    Колебания цены EUR/USD за 100 минут. Период дискретизации 1 минута.

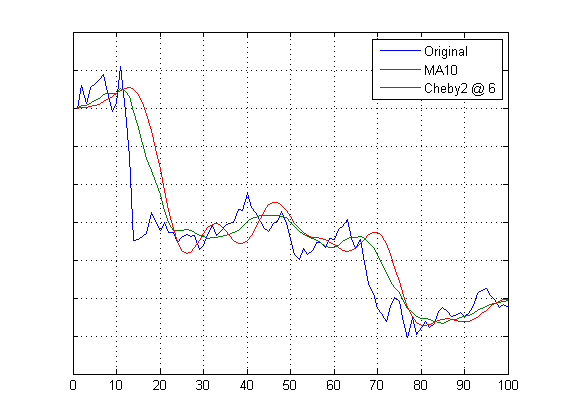
    Синяя линия - исходные колебания, зеленая - МА10, красная - результат воздействия фильтра Чебышева. Фильтр Чебышева настроен на фильтрацию частот, начиная с граничной частоты среза МА10 по уровню -20 дБ (период колебаний <6 периодов дискретизации) и уровень рабочего усиления в диапазоне фильтрации -40 дБ (1/100). Колебания красной линии показывают, что плавный спад ЧХ МА10 ослабляет ряд колебаний с периодами в диапазоне 12..6 периодов дискретизации.

    Возвращаясь к вопросам детерминирования уровня шума, становится возможным простейшими средствами проводить осмысленный анализ спектрального состава сигнала.

    У нас есть ряд мыслей о практическом использовании фильтрации и знаний о спектральном составе, и мы надеемся их представить на суд общественности.