Источник:
    http://cact.csuohio.edu/index.php?option=com_docman&task=doc_download&gid=151&Itemid=70

Zhiqiang Gao, Thomas A. Trautzsch and James G. Dawson

Устойчивая самонастраивающаяся система управления на основе нечеткой логики для регулирования температуры в производственных процессах

Перевод с английского Роик В.С.

Аннотация

Была разработана система управления замкнутого цикла, включающая нечеткую логику, для класса промышленных проблем управления, связанных с температурой. Была предложена уникальная структура контроллера нечеткой логики с эффективной реализацией и маленькой базой правил, которая может быть легко реализована в уже существующих промышленных контроллерах. Данная структура показала потенциал FLC как в программном моделировании, так и при промышленной установке. Он включает компенсацию за термические изменения в системе, которая имеет дело с неизвестными и переменными задержками, работу при совсем разных температурных точках без перенастройки и т.д. Это достигается за счет реализации в FLC классической стратегии управления и механизма адаптации, для компенсации динамических изменений в системе. Предложенный FLC был применен к двум различным температурным процессам, при этом, производительность и улучшения устойчивости наблюдались в обоих случаях. Кроме того исследована устойчивость FLC , и установлена защита.

I. Введение

В то время как современная теория управления оказала скромное влияние на практику, управление при помощи нечеткой логики быстро завоевывало популярность среди практикующих инженеров. Эта увеличенная популярность может быть приписана факту, что нечеткая логика обеспечивает мощный механизм, который позволяет инженерам включать рассуждения человека в алгоритм управления. В противоположность современной теории управления, проектирование на основе нечеткой логики не базируется на математической модели процесса. Разработанный контроллер, использующий нечеткую логику, реализует человеческие рассуждения, которые могут быть запрограммированы на языке нечеткой логики (функции принадлежности, правила и интерпретация правила).

Промышленные интересы к нечеткому управлению, как засвидетельствовали многие публикации в литературе по тематике управления, создали понимание ее увеличивающейся важности академическим сообществом. Быстрое увеличение вычислительных мощностей современной цифровой технологии управления делают FLC жизнеспособным и привлекательным во многих отраслевых секторах. Самонастраивающийся модель, основанная на нечеткой логике была исследована многими исследователями применительно к различным проблемам. Результатами, о которых сообщают в литературе, обычно являются специфические и не легко переносимые приложения. Сложность алгоритма управления и отсутствие интуиции в настройках ограничивает сферу применения приложений для многих предлагаемых методов.

В этой статье мы концентрируемся на управлении при помощи нечеткой логики как на эффективной альтернативе существующему пропорциональному-интегралпроизводному (PID) методу, который широко используется в отрасли. Контроллер, включая самонастраивающийся алгоритм, должен быть прост для понимания и реализации для практикующих инженеров. Рассмотрим универсальное температурный метод управления, показанный на рисунке 1.

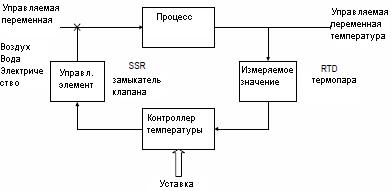
Рис. 1 Типичная производственная проблема управления температурой

Температура измеряется подходящим датчиком, такими как термопары, резистивные тепловые устройства (RTDs), терморезисторы, и т.д. и преобразовывается в сигнал, приемлемый для контроллера. Контроллер сравнивает температурный сигнал с требуемой установленной точкой температуры и приводит в действие элемент управления. Элемент управления изменяет регулируемую переменную, чтобы изменить количество тепла, добавляемого или взятого от процесса. Цель контроллера состоит в том, чтобы отрегулировать температуру настолько близко насколько возможно к установленной точке.

Для того, чтобы протестировать новые алгоритмы управления, основанные на нечеткой логике, в данном исследовании использовались два процесса температурного регулирования. Один использует горячую и холодную воду в качестве регулируемой переменной, и клапана как элемент управления, другой использует электричество как источник питания к нагревателю, приводимому в действие твердотельным реле (SSR). Новые алгоритмы были протестированы экстенсивно и на моделировании и на аппаратных тестах.

A. Обоснование

В настоящий момент, классическое PID (Пропорционально-интегрально- производное) управление широко используется вместе с его вручную настроенными коэффициентами усиления, основанными на количестве тепла и установленных точках температуры. Оборудование с большими теплоемкостями требует различные усиления PID в отличии от оборудования с небольшими теплоемкостями. Кроме того, работа оборудования по широким диапазонам температур (от 140º до 500º) требует, чтобы различные усиления на нижнем и на более высоком уровне диапазона температуры избегали проскакивания и колебания. Это необходимо, так как даже краткое температурное проскакивание, например, может инициировать аварийные сигналы, неприятности и дорогостоящие остановки контролируемого процесса. Обычно, настройка PID-констант для управления температурой большого процесса является дорогостоящей и трудоёмкой. Задача усложняется, когда иногда вводятся неправильные PID-константы из-за нехватки понимания процесса управления температурой.

Трудность при таких проблемах состоит в переменных временных задержках, которые существуют во многих подобных системах. Изменения в производстве, разработка нового продукта и физические ограничения помещают температурный датчик RTD в различные местоположения, вызывая переменные задержки (потерю времени) в системе.

Также известно, что PID-контроллеры показывают низкую эффективность, когда используются в системах, которые содержат неизвестную нелинейность, такие как мертвые зоны насыщения и гистерезис. Далее подразумевается, что многие процессы управления температурой являются нелинейными. Равные инкременты ввода тепла, например, не обязательно производят равные инкременты в повышении температуры во многих процессах - типичное явление нелинейных систем.

Сложность этих проблем и трудностей состоит в реализации стандартных контроллеров; для устранения изменений в настройке PID нам необходимо исследовать интеллектуальные методики управления, такие как нечеткая логика как решение проблемы управления системами, в которых должны быть рассмотрены время задержки, нелинейности, и ручные настройки процедур.

B. Проблема временных задержек и существующие решения

Чтобы изучить проблему управления температурой классическими методиками, рассмотрим упрощенную блок-схему рисунка 2, которая используется вместо рисунка 1, где C(s) - контроллер и G(s)e-sτ - оборудование с чистой временной задержкой τ.

Рис. 2 Система управления температурой замкнутого цикла

Было разработано много схем компенсаций задержки и прогноза, и/или улучшено с модификациями, как показано в [7-12]. Производительность устройства прогнозирующего управления Смита (SPC) была экспериментально изучена в [8]. Данное исследование показывает, что система хорошо работает, если модель процесса точна, но производительность быстро уменьшается вместе с погрешностью в параметрах процесса и задержкой. Ясно, что прогнозирующая компенсация Смита для неизвестной или переменной задержки больше не является жизнеспособным методом.

В литературе недавно появилось несколько методов разработки модели управления для систем с изменением задержек, например, оценочныйй и самонастраивающийся метод, предложенный Brone и Harris [10], переменный структурный контроллер Shu и Yan [11], а также описание модели адаптивного подхода Liu и Wang [12].

Для систем с большими временными задержками большинство подходов к проектированию использует механизм прогноза в качестве части контроллера, чтобы моделировать процесс для данных системных параметров и временных задержек.

В хорошо известном прогнозирующем устройстве Смита [7], выход контроллера подается через модели процесса с задержкой, и процесс без задержки, соответственно. Различие выходных сигналов добавлено к фактическому выводу оборудования и затем выведено к контроллеру, таким образом, позволяя контроллеру действовать на прогноз вывода оборудования.

Использование этого известного метода компенсации задержки даже на простом оборудовании первого порядка в контроллере PID промышленного стандарта, таком как одноцикличный контроллер Bailey’s Infi-90 все еще нелегкая задача. Должны быть определены параметры прогнозирующего устройства, включая усиление оборудования, временную константу, и задержку, в дополнение к трем параметрам PID. Эти шесть параметров используются в прогнозирующей настройке компенсатора и операционной сложности даже на самом простом оборудовании. Дополнительная сложность прогнозирующего устройства Смита - основная причина, из-за которой отрасль все еще использует непрогнозирующий PI или PID-управление для настраиваемых методов использования задержки, таких как метод Зиглер-Николса.

C. Управление при помощи нечеткой логики

Нечеткое управление - привлекательная альтернатива стандартным способам управления, при которых системы следуют за некоторой общей рабочей характеристикой, детальное понимание процесса неизвестно, или традиционные модели систем становятся чрезмерно сложными [6]. Возможность качественного получения атрибутов системы управления на основе наблюдаемых явлений - основная функция нечеткого управления. Эти аспекты нечеткого управления демонстрировались в различной исследовательской литературе, см. [13-15,18,19], и в коммерческих продукты от поставщиков таких как Reliance Electric and Omron. Возможность нечеткой логики получать системную динамику качественно, и выполнять эту качественную идею в реальном времени - привлекательная функция для систем управления температурой.

Конечно, у нечеткой логики управления есть свои собственные ограничения. Аналитическое исследование нечеткой логики все еще запаздывает по сравнению с ее реализацией; много работы все еще впереди, особенно в области устойчивости и анализа эффективности. Кроме того, модель нечеткого управления, как решение практических задач, является проблемозависимой, и адаптация существующего контроллера нечеткой логики к различной проблеме управления не является прямой. Доступные средства проектирования, такие как Fuzzy Toolbox, предоставленная Mathworks Inc., обычно требуют дальнейших улучшений прежде, чем они станут приемлемыми для инженеров управления. В этой статье исследуется обоснованность нечеткого управления, как альтернативного подхода в приложениях управления температурой.

II. Модель управления на основе нечеткой логики

FLC, разработанный здесь, имеет два входа и один выход. Два входа - отклонение от установленной ошибки e (k), и коэффициент ошибок, Δe (k). FLC реализован в форме дискретного времени, используя нулевой порядок удерживания, как показано в рисунке 3a. Функциональная структура нечеткого контроллера показана на рисунке 3b.

A. Фаззификация/Дефаззификация

Фаззификация и дефаззификация включают отображение нечетких переменных, представляющих интерес, для «четких» чисел, используемых системой управления. Фаззификация преобразовывает числовое значение для ошибки, e (k), или коэффициента ошибки, Δe (k), в лингвистическое значение такое как «положительное большое» со степенью принадлежности. Дефаззификация берет нечеткий вывод правил и генерирует «четкое» числовое значение, используемое в качестве управляющий вход для оборудования.

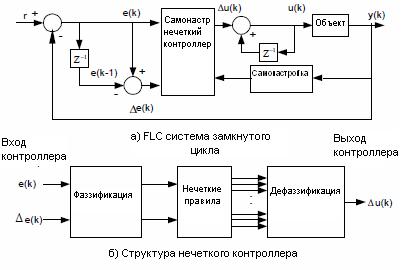
Рис. 3 Система управления, основанная на нечеткой логике

Функции принадлежности FLC определены по диапазону из входных и выходных значений переменных и лингвистически описывают универсум переменной, как показано на рисунке 4. Треугольная входная принадлежность функционирует для лингвистических переменных «нуль», «малый», «средний», и «большой», настройка их принадлежности центрирует значения в 0, 0.2, 0.35, и 0.6, соответственно. Универсум для e и для Δe может быть нормализован от-1 до 1 в случае необходимости. Левая и правая половина треугольной принадлежности функционирует для каждой выбранной лингвистической метки, чтобы предоставить перекрытие принадлежности смежными функциями принадлежности. Прямая линия вывода функций принадлежности функционирует для меток «нуль», «маленький», «средний», и «большой», определена как показано в рисунке 4 с конечными точками 10, 30, 70, и 100 % максимума вывода, соответственно. Обе входные и выходные переменные функции принадлежности симметричны относительно источника.

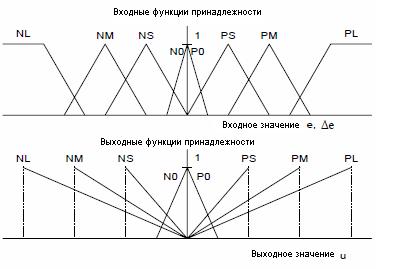
Рис. 4 Нечеткие функции принадлежности

Выбор числа функций принадлежности и их начальных значений основан на знании процесса и интуиции. Основная идея состоит в том, чтобы определить разделы по области работы оборудования, которые соответственно представят переменные процесса.

Как только входные переменные фаззифицированы и проходят нечеткую базу правил, которая описана ниже, тогда выход правил агрегируется и дефаззифицируетя. Агрегация результатов нечетких правил логически суммирует все выходные нечеткие множества. Затем, генерируется сигнал числового программного управления. Типичная формула для этой цели - так называемый центроидный метод [6], в котором управляющий сигнал вычисляется следующим образом:

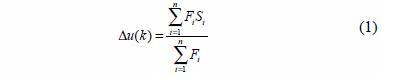
где Fi - степень принадлежности, и S - одноэлементная позиция функции принадлежности. Этот метод используется в нашем исследовании моделирования в разделе III. Для промышленной реализации, показанной в разделе V, однако, используется метод дефаззификации наименьшего максимума (SOM), где управляющий сигнал получен как:

Это потому, что SOM дефаззификация менее интенсивна в вычислительном отношении чем центроидное вычисление.

B. Разработка правил

Наша стратегия разработки правил для систем с задержкой должна отрегулировать полный коэффициент усиления по петле, чтобы достигнуть требуемого ответного шага. Вывод FLC основан на текущем вводе, e (k) и Δe (k), без знаний предыдущих входных и выходных данных или любой формы модели прогнозирующего устройства. Основная идея состоит в том, что, если FLC не разработан со специальными знаниями математической модели оборудования, то он не будет зависеть от этого. Правила, разработанные в этой статье, в состоянии компенсировать изменение задержек в реальном времени, настраивая выходные функции принадлежности FLC, основанные на работе системы.

Правила FLC разработаны на основе понимания того, как стандартный контроллер работает на систему с фиксированной задержкой. Правила разделены на два уровня: первый уровень правил FLC подражает действиям простого контроллера PID при фиксированной и известной задержке задержке; второй уровень правил имеет дело с проблемой, когда задержка является неизвестной и переменной.

В разработке правил первого уровня рассмотрено оборудование первого порядка, G(s)e-sτ, где G(s)=a/(s+a). При проектировании PID сделаны следующие предположения:

• задержка τ известна;
• время повышения, tτ, или эквивалентное время известно, расположение поля известно;
• tτ значительно меньше чем τ;
• интервал выборки – T_s

Стандартный контроллер типа PI в инкрементной форме задается:

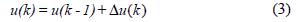
где Δu (k) =f (e, Δe) вычислен алгоритмом PI дискретного времени. Этот алгоритм управления был применен к оборудованию первого порядка с задержкой. Начальная настройка параметров PI была выполнена при использовании метода Зиглер-Николса. Полученный ответный шаг имеет приблизительно 20%-ое проскакивание для фиксированной задержки.

Затем был установлен управляющий нечеткий закон где Δu (k) =F (e, Δe), выход FLC для kth интервала выборки, заменяет f (e, Δe) в инкрементном контроллере, описанном в (3). Были разработаны правила и функции принадлежности FLC , используя интуитивное понимание того, что контроллер PI делает при фиксированной задержке в системе первого порядка. Они обобщали то, что PI-контроллер делает для каждой комбинации e и Δe в 12 правилах как показано в таблице 1.

Таблица 1 Правила управления FLC

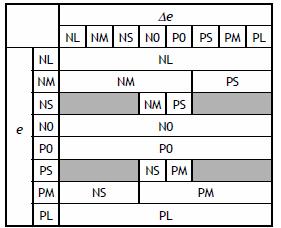
Выход из каждого правила может быть обработан как нечеткий одиночный элемент. Управляющее действие FLC - комбинация вывода каждого правила, используя средневзвешенную величину метода дефаззификации и может быть рассмотрен как центр тяжести нечеткого множества выходных одиночных элементов.

C. Настройка функций принадлежности в стадии проектирования

С тех пор пока есть немного установленного теоретического руководства, настройка правил и функций членства в стадии проектирования - в значительной степени представляет итеративный процесс, основанный на интуиции. Функции принадлежности были настроены по критериям устойчивости, таких как время повышения, проскакивание, и установившаяся ошибка, полученных позже из IV раздела, основанных на наблюдениях за работой системы.

Число функций принадлежности может изменяться, чтобы обеспечить необходимое разрешение. Отметим, что число правил может вырасти по экспоненте в зависимости от числа входного увеличения функций принадлежности. Входная принадлежность функционирует для e и Δe генерирует 64 комбинации, которые могут быть сгруппированы в двенадцать областей, соответствующих каждому правилу в таблице 1.

Центр и наклоны входных функций принадлежности в каждой области скорректированы так, чтобы соответствующее правило обеспечило соответствующее действие управления. В случае, если, когда два или больше правила запущены одновременно, доминирующее правило, правило, соответствующее высокому классу членства, настраивается в первую очередь. Изменение выходной функции принадлежности корректирует содействие правил относительно выходного универсума. После того, как входная настройка правила принадлежности завершена, выполняется подстройка выходных функций принадлежности, чтобы достигнуть требуемой производительности.

Хотя этот FLC создан при условии, что задержка фиксирована и известна, единственный элемент контроллера, который является функцией задержки, является универсумом для вывода. Ниже показано, что FLC может выполнять некоторую корректировку и создавать дополнительные правила, для адаптации к неизвестной природе или изменению в задержке.

D. Самонастройка

Структура FLC, представленная выше, может быть непосредственно изменена, чтобы компенсировать изменения в динамике оборудования и переменных задержках, добавляя второй уровень самонастройки правил к FLC. В случае изменения задержки, усиление FLC должно быть скорректировано, чтобы сместить эффекты изменений в задержке. Было замечено, что максимальное действие усиления или управления обратно пропорционально задержке. Поэтому, если задержка увеличивается, мы должны уменьшить усиление FLC, чтобы уменьшить действие управления, и наоборот. Основываясь на этом отношении, работа системы может контролироваться вторым уровнем правил, который адаптирует выходные функции принадлежности первого уровня правил, улучшая производительность нечеткого контроллера.

Будем считать выходную функцию принадлежности настроенной для номинальной задержки. Когда истинная системная задержка больше чем номинальная задержка, действие управления, определенное номинальной задержкой, заставляет выход управления быть слишком большим для истинной системы. Это условие эффективно увеличивает усиление контроллера, и как различие между истиной и номинальная задержка становится большой, могут возникнуть проблемы устойчивости системы. Наоборот, когда истинная задержка меньше чем номинальная задержка, усиление контроллера будет слишком маленьким, и система становится «вялой».

Выходные функции принадлежности (см. рисунок 4) FLC определены с точки зрения максимального действия управления. Жизнеспособный механизм, чтобы компенсировать переменную задержку должен скорректировать размер действия управления под предположением, что число правил управления остается фиксированным, и лингвистическая стратегия управления допустима для различных значений задержки. Эти условия разумны для данных известных параметров оборудования; разработанная стратегия управления основана на использовании оборудования с задержкой.

Чтобы скорректировать FLC в реальном времени для систем с изменением задержки, был добавлен второй уровень из шести правил как механизм адаптации, чтобы изменить выходную функцию принадлежности, используемую первыми правилами уровня с масштабным коэффициентом. Это эффективно изменяет выходной универсум управления FLC (то есть, максимальное действие управления), основанный на производительности системы. Эти правила корректируют выход FLC, основанный на времени повышения и проскакивании. Проскакивание контролируется и классифицируется как большое (L), среднее (M), и маленькое (S). Замечено что изменения в проскакивании показывает изменения в задержке. Более длинная задержка приводит к большему проскакиванию. Такие эффекты могут быть облегчены, посредством уменьшения выходного масштабного коэффициента соответственно. Повышение времени работы классифицировано как Очень Медленное (VS), среднее, Медленное (MS), и Немного Медленное (SS), а увеличение выходного масштабного коэффициента может помочь ускорить ответ.

Стратегия проектирования второго уровня правил основана на двух различных аспектах отслеживания производительности, то есть, время повышения и проскакивание, вычисленное от (e, Δe). Правила второго уровня перечислены в таблице 2. Они контролируют ответ оборудования и уменьшают или увеличивают выходной универсум контроллера FLC. Определены нечеткие функции принадлежности, используя конфигурацию принадлежности, подобную стратегии управления в рисунке 3. Правила корректировки выполняют два действия; они уменьшают усиление FLC, когда оборудование значительно промахивается по требуемому ответу, и увеличение усиления, когда повышение времени работы является медленным.

Примечание: В этом разделе представлена уникальная нечеткая система управления. Хотя PI-контроллер используется в качестве направляющей линии для настройки FLC, то ни в коем случае не ограничивает его возможность выполнения более сложных задач. Подобные подходы могут быть использованы для настройки FLC, который подражает более сложным контроллерам.

Особое значение здесь уделяется работе с неизвестной динамикой и различными проблемами с временными задержками, с которыми мы имели трудности при использовании аналитических подходов. В частности, способность к самонастройке, продемонстрированная в предложенной модели FLC, хоть и ограничена узким классом проблем с большими изменениями уставок, показывает потенциал объединения интеллекта человека с управляющей стратегией.

Таблица 2 Выходное регулирование FLC

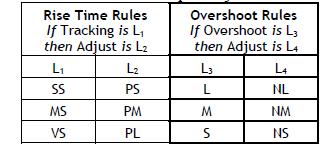
III. Программное моделирование

Спроектированный выше FLC был смоделирован для управления температурой в резервуаре с жидкостью, показанного на рис. 5. Температура резервуара с текучей средой с постоянной скоростью потока на входе и на выходе контролируется за счет подстройки температуры приходящего потока. Температура приходящего потока задается смесительным клапаном, который регулирует соотношение холодной и горячей жидкости от транспортной линии до резервуара. Расстояние между смесительным клапаном и транспортной линией, из которой жидкость вытекает в резервуар, показывает классическую транспортную задержку в трубопроводах. Температура/давление жидкостей также будет влиять на задержку.

Рис. 5 Управление температурой в резервуаре

Функция для проблемы температурного контроля резервуара с жидкостью на рис.5 выглядит следующим образом:

где Т_е = температура в резервуаре, Т_ес = температура на выходе смесительного клапана; τ = временная задержка транспортировки по трубопроводу, a = m/M, m = скорость потока жидкости, и М = масса жидкости в резервуаре.

А. Результаты моделирования

FLC применялся для оборудования, описанного в выражении (4) с а=1. При условии, что горячий и холодный приток поступает в смесительный клапан при постоянном давлении, временная задержка транспортировки также будет постоянной. Наоборот, если давление горячего и холодного притока непостоянно, транспортная задержка будет также различаться. Различные аспекты временных задержек данной системы исследованы в следующих моделирующих испытаниях.

Рис. 6 Сравнение PID, SPC и FLC

Результаты моделирования получены с помощью 18 правил FLC, 12 правил первого слоя таблицы 1, которые обеспечивают управленческую стратегию, и 6 правил второго слоя таблицы 2, которые подстраивали управляющую выходную функцию принадлежности универсума рассуждений, основанного на работе системы. Для сравнительных целей графики моделирования содержат обычный PID контроллер, прогнозирующее управление Смита (SPC), и нечеткий алгоритм. PID, SPC и FLC были настроены для оборудования с 10-секундной временной задержкой, с откликом, показанным наверху рисунка 6. Как ожидалось, у SPC был самый быстрый отклик при наличии точной модели оборудования и известной временной задержки, но PID и FLC обеспечивают хорошую производительность при увеличении времени и проскакивании и недостаточности предсказывающего алгоритма. Середина и конец рисунка 6 показывают, как реагируют контроллеры на увеличение временной задержки, использованной для настройки контроллеров. FLC алгоритм быстрее адаптируется к более длинным временным задержкам и предоставляет устойчивый отклик, в то время, как PID контроллер приводит систему в неустойчивое состояние, а SPC колебается вокруг окончательного значения до тех пор, пока не сгенерируется ошибка несоответствия с параметром временной задержки, используемом в модели оборудования.

Исходя из моделирования, ясно, что SPC предоставляет лучший отлик с точными моделями оборудования и задержками. В присутствии неизвестной или возможной изменяющейся временной задержки, предложенная модель FLC показывает существенное улучшение производительности и сохранение стабильности по сравнению со стандартными методами SPC и PID. Отметим, что здесь предполагается, что задержка неизвестна и изменчива во времени. Если это не тот случай, тогда может быть использован «адаптивный» PID с предсказательным устройством Смита, где задержка оценивается в режиме on-line, как было отмечено анонимным рецензентом.

Выводы:

В отличие от нечетких контроллеров с сотнями или даже тысячами правил, используемых в компьютерных системах, уникальный FLC, используя малое количество правил и простую реализацию, предлагает решение класса проблем, связанных с управлением температурой при неизвестной динамике или переменных временных задержках, так часто встречающихся в промышленности. Дополнительно, используемые на данный момент промышленные контроллеры могут быть легко запрограммированы при помощи FLC. FLC был впервые промоделирован для проблемы управления температурой в жидкостном резервуаре с довольно обещающими результатами.

Литература:

1. James Dawson, "Fuzzy Logic Control of Linear Systems with Variable Time Delay," M.S. Thesis, Cleveland State University, June 1994.

2. Thomas A. Trauztch, “Self-Tuning Temperature Control Using Fuzzy Logic, M.S. Thesis, Department of Electrical Engineering, Cleveland State University, June 1996

3. David J. Elliott, "Fuzzy Logic Positional Servo Motor Control Development Platform", M.S. Thesis, Department of Electrical Engineering, Cleveland State University, June 1997.

4. Wilfred Nonnenmacher, Fuzzy Logic Position Control of a Servo Motor, M.S. Thesis, Department of Electrical Engineering, Cleveland State University, April 1997.

5. Nitin Dhayagude, Zhiqiang Gao and Fouad Mrad, "Fuzzy Logic Control of Automated Screw Fastening", Journal Robotics and Computer Aided Manufacturing, Vol. 12, No.3 pp. 235-242, 1996

6. K. Passino and S. Yurkovich, Fuzzy Control, , Addison-Wesley, 1998.

7. O.J.M. Smith, "A Controller to Overcome Dead Time" ISA Journal, No. 2,28, February 1959.

8. P.S. Buckly, "Automatic Control of Processes with Dead Time," Proc. IFAC World Congress, Moscow, 1960, p33-40.

9. J.E. Marshall, "Control of Time Delay Systems," Stevenage, UK; NY P. Peregrinus, c1979.

10. Q. Brone, and S. Harris, "Varying Time Delay Estimation and Self-Tuning Control," Proceedings of the 1991 American Controls Conference, v2, p1740-1741.

11. K. Shu, and J. Yan, "Robust Stability of Uncertain Time Delay Systems and its Stabilization by Variable Structure Control," Int. Journal of Control, 1993, v57 n1, p237-246.

12. G.P. Liu, and H. Wang, "Adaptive Controller for Continuous-Time Systems with Unknown Varying Time Delay," 1991 Int. Conf. of Cont. IEE Conf. Pub. v2, n332, p1084-1088.

13. C.C. Lee, "Fuzzy Logic in Control Systems: Fuzzy Logic Controller -- Parts 1 & 2 " IEEE Trans. on Sys. Man, and Cybernetics, Vol 20, No.2, pp404-435 March/April 1990.

14. P.J. King, and E.H. Mamdani, "The Application of Fuzzy Control Systems to Industrial Processes," Automatica, v11, p235-242, 1977.

15. S. Chiu, S. Chand, D. Moore, and A. Chaudhary, "Fuzzy Logic for Control of Roll and Moment for a Flexible Wing Aircraft", IEEE Cont, Sys. Mag. Vol. 11,No. 4, ’91, pp42-48.

16. J.A. Bernard, "Use of a Rule-Based System for Process Control", IEEE Cont. Sys. Mag. pp3-13, October 1988.

17. J. Litt, "An Expert System to Perform On-Line Controller Tuning", IEEE Cont. Sys. Mag, pp18-23, April 1991.

18. S. Tzafestas, and N. Papanikolopoulos, "Incremental Fuzzy Expert PID Control," IEEE Trans. on Industrial Electronics, Vol. 37, pp365-371, October 1990.

19. P. Oliveria, P. Lima, and J. Sentierio, "Fuzzy Supervision of Direct Controllers," Proc. 5th IEEE International Symposium on Intelligent Control, pp638-643, 1990.

20. Pekka Isomursu, Tapio Rauma, "Self-tuning fuzzy logic controller for temperature control of superheated steam", IEEE International Conference on Fuzzy Systems v 3 1994 p.1560-1563.

21. Yongmei Wang, Douglas J. Birdwell, "Nonlinear PIDtype controller utilizing fuzzy logic" Proc IEEE IFAC Jt Symp Comput Aided Control Syst Des 1994 p.89-94.

22. Kam-Wing Li, Burhan Turksen; Kenneth Smith, “FPGA implementation of a self-tuned fuzzy controller” Biennial Conference of the North American Fuzzy Information Processing Society - NAFIPS 1996 p.285-288.

23. Seok-Yong Oh, Dong-Jo Park, “Self-tuning fuzzy controller with variable universe of discourse”, Proceedings of the IEEE International Conference on Systems, Man and Cybernetics v 3 1995 p.2628-2632.

24. J. Slotine, W. Li, "Applied Nonlinear Control," Prentice Hall, Englewood Cliffs, NJ, 1991.

25. R.R. Mohler, "Nonlinear Systems: Volume I, Dynamics and Control," Prentice Hall, Englewood Cliffs, NJ, 1991.