Squarified Treemaps

Mark Bruls, Kees Huizing, and Jarke J. van Wijk

Eindhoven University of Technology

---

Source of information: http://www.win.tue.nl/~vanwijk/stm.pdf

---

Abstract.

An extension to the treemap method for the visualization of hierarchi- cal information, such as directory structures and organization structures, is pre- sented. The standard treemap method often gives thin, elongated rectangles. As a result, rectangles are difficult to compare and to select. A new method is presented to generate lay-outs in which the rectangles approximate squares. To strenghten the visualization of the structure, shaded frames are used around groups of related nodes.

1 Introduction

Hierarchical structures of information are everywhere: directory structures, organization structures, family trees, catalogues, computer programs, and so on. Small hierarchical structures are effective to locate information, but the content and organization of large structures is harder to grasp. We present a new visualization method for large hierarchi- cal structures: Squarified Treemaps. The method is based on Treemaps, developed by Shneiderman and Johnson [9, 6]. Treemaps are efficient and compact displays, which are particularly effective to show the size of the final elements in the structure. In a previous paper [10] we introduced Cushion Treemaps, which provide shading as an extra cue to emphasize the hierarchical structure. In this paper we attack another problem of stan- dard treemaps: the emergence of thin, elongated rectangles. We propose a new method to subdivide rectangular areas, such that the resulting subrectangles have a lower aspect ratio. These rectangles use space more efficiently, are easier to point at in interactive en- vironments, and are easier to estimate with respect to size. Because the resulting struc- tures are somewhat harder to grasp, we also introduce an improved method to visualize nested structures. A variant on nested treemaps is presented, where the rectangular en- closures have been replaced by shaded frames. The combination of these two methods leads to displays of hierarchical structures that are efficient and easy to understand.

In section 2 we discuss existing methods to visualize hierarchical structures. The new method for improved subdivision is presented in section 3. The shaded frames are de- scribed in section 4. Finally, we discuss the results in section 5.

2 Background

Many methods exist to browse through and to display hierarchical information struc- tures, or, for short, trees. File browsers are the best known example. Usually a listing ofthe files and directories is used, where the levels in the hierarchy are shown by means of indentation. The number of files and directories that can be shown simultaneously is limited, which is no problem if one knows what to search for. However, if we want to get an overview, or want to answer a more global question, such as: ”Why is my disk full?”, scrolling, and opening and closing of subdirectories have to be used intensively. During this process it is hard to form a mental image of the overall structure [3].

Many techniques have been proposed to visualize such structures more effectively. An important category are node and link diagrams (fig. 1(a)). Elements are shown as nodes, relations are shown as links from parent to child nodes. Sophisticated techniques have been presented to improve the efficiency and aesthetic qualities of such diagrams, both in 2D and in 3D [7, 5, 1, 2, 8]. Such diagrams are very effective for small trees, but usually fall short when more than a couple of hundred elements have to be visualized si- multaneously. The main reason for this limitation is simply that node and link diagrams use the display space inefficiently: Most of the pixels are used as background. Treemaps

[9, 6] were developed to remedy this problem. The full display space is used to visualize the contents of the tree. Here we present an overview of the concept, an in depth treat- ment is given in the original references. Figure 1(b) shows an example. Each node (as shown in the tree diagram) has a name (a letter) and an associated size (a number). The size of leaves may represent for instance the size of individual files, the size of non-leaf nodes is the sum of the sizes of its children. The treemap is constructed via recursive subdivision of the initial rectangle. The size of each sub-rectangle corresponds to the size of the node. The direction of subdivision alternates per level: first horizontally, next vertically, etcetera. As a result, the initial rectangle is partitioned into smaller rectangles, such that the size of each rectangle reflects the size of the leaf. The structure of the tree is also reflected in the treemap, as a result of its construction. Color and annotation can be used to give extra information about the leaves.

Treemaps are very effective when size is the most important feature to be displayed. Figure 2(a) shows an overview of a file system: 1400 files are shown and one can effort- lessly determine which are the largest ones.

However, treemaps have limitations [4]. One problem is that treemaps often fall short to visualize the structure of the tree. The worst case is a balanced tree, where each parent

has the same number of children and each leaf has the same size. The treemap degener- ates here into a regular grid. As an example, figure 2(b) shows an (artificial) organization chart, modeled after the structure of our university. Six levels in the hierarchy are shown, the final 3060 rectangles denote individual employees. In a previous paper [10] we have shown how shading can be employed to improve the perception of structure.

In this paper we study another problem of treemaps. In both examples thin, elon- gated rectangles emerge as a result of the straightforward subdivision technique of stan- dard treemaps. All children on a level are treated the same, hence the presentation of a small file is degraded when compared to its larger siblings (think of a large Unix home directory with a small .cshrc in the top level). The presentation of all nodes and leaves as more square-like rectangles has several advantages:

– display space is used more efficiently. The number of pixels to be used for the border is proportional to its circumference. For rectangles this number is minimal if a square is used;

– square items are easier to detect and point at, thin rectangles clutter up and give rise to aliasing errors;

– comparison of the size of rectangles is easier when their aspect ratios are similar;

– the accuracy of the presentation is improved. A rectangle with a prescribed width of, say, 300 pixels, can only present sizes in coarse steps.

These advantages inspired us to study alternative subdivision techniques, where the aim is to use rectangles that are nearly square for the nodes and leaves. In a late stage of the writing of this paper we found that we are not exceptional in this interest. The concept of squarification has been applied independently of our work for a very clear and effective visualization of a stock market [11].

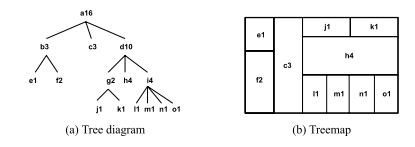
3 Squarification

How can we tesselate a rectangle recursively into rectangles, such that their aspect-ratios (e.g. max( height = width ; width = height )) approach 1 as close as possible? The number ofall possible tesselations is very large. This problem falls in the category of NP-hard prob- lems. However, for our application we do not need the optimal solution, a good solution that can be computed in short time is required.

We have experimented with many different algorithms. In this section we present a method that (empirically) turned out to give the best results. The key idea is based on two notions. First, we do not consider the subdivision for all levels simultaneously. This leads to an explosion in computation time. Instead, we strive to produce square-like rect- angles for a set of siblings, given the rectangle where they have to fit in, and apply the same method recursively. The startpoint for a next level will then be a square-like rect- angle, which gives good opportunities for a good subdivision. Second, we replace the straigthforward subdivision process for a set of siblings of the standard treemap tech- nique (width or height is given, rectangle is subdivided in one direction) by a process that is similar to the hierarchical subdivision process of the standard treemap.

We present our method first with an example, followed by a description of the com- plete algorithm.

3.1 Example

Suppose we have a rectangle with width 6 and height 4, and furthermore suppose that this rectangle must be subdivided in seven rectangles with areas 6, 6, 4, 3, 2, 2, and 1 (figure 3). The standard treemap algorithm uses a simple approach: The rectangle is subdivided either horizontally or vertically. Thin rectangles emerge, with aspect ratios of 16 and 36, respectively.

The first step of our algorithm is to split the initial rectangle. We choose for a hori- zontal subdivision, because the original rectangle is wider than high. We next fill the left half. First we add a single rectangle (figure 4). The aspect ratio of this first rectangle is 8/3. Next we add a second rectangle, above the first. The aspect ratios improve to 3/2. However, if we add the next (area 4) above these original rectangles, the aspect ratio of this rectangle is 4/1. Therefore, we decide that we have reached an optimum for the left half in step two, and start processing the right half.

The initial subdivision we choose here is vertical, because the rectangle is higher than wide. In step 4 we add the rectangle with area 4, followed by the rectangle with area 3 in step 5. The aspect ratio decreases. Addition of the next (area 2) however does not improve the result, so we accept the result of step 5, and start to fill the right top partition.

These steps are repeated until all rectangles have been processed. Again, an optimal result can not be guaranteed, and counterexamples can be set up. The order in which the rectangles are processed is important. We found that a decreasing order usually gives the best results. The initially large rectangle is then filled in first with the larger subrectan- gles.

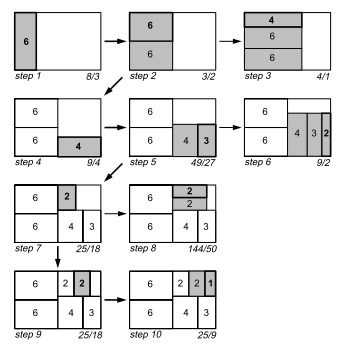
3.2 Algorithm

Following the example, we present our algorithm for the layout of the children in one rectangle as a recursive procedure squarify. This procedure lays out the rectangles in horizontal and vertical rows. When a rectangle is processed, a decision is made between two alternatives. Either the rectangle is added to the current row, or the current row is fixed and a new row is started in the remaining subrectangle. This decision depends only on whether adding a rectangle to the row will improve the layout of the current row or not.

We assume a datatype Rectangle that contains the layout during the computation and is global to the procedure squarify. It supports a function width() that gives the length of the shortest side of the remaining subrectangle in which the current row is placed and a function layoutrow() that adds a new row of children to the rectangle. To keep the de- scription simple, we use some list notation: ++ is concatenation of lists, [x] is the list containing element x , and [] is the empty list. The input of squarify() is basically a list of real numbers, representing the areas of the children to be laid out. The list row con-tains the rectangles that is currently being laid out. The function worst() gives the highest aspect ratio of a list of rectangles, given the length of the side along which they are to be laid out. This function is further discussed below.

Let a list of areas R be given and let s be their total sum. Then the function worst is defined by:

Since one term is increasing in r and the other is decreasing, this is equal to

where r + and r , are the maximum and minimum of R . Hence, the current maximum and minimum of the row that is being laid out.

Applying this algorithm to the data sets of figure 2 results in figure 5. This shows clearly that the algorithm is succesful in the sense that the rectangles are far less elon- gated and that the black areas with cluttered rectangles have disappeared. However, they also show that the hierarchical structure is far less obvious than with the standard treemap algorithm. The alternating directions scheme aids in providing the viewer with direct cues on the structure, whereas with a less regular scheme these visual cues disappear. When the sizes vary strongly (figure 5(a)), a subtle cue is provided. From the lower-left corner to the upper-right corner the size of the rectangles decreases, which shows more or less which child-nodes have the same parent. However, when the leaves have the same size (figure 5(b)), this cue is not present.

One way to improve the visualization of the structure is to use cushions (figure 6). However, the global structure is still not obvious, for instance in figure 6(b) it is hard to detect the seven nodes at the highest level. Hence, we have studied additional methods to emphasize the structure.

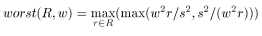
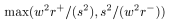
4 Frames

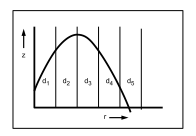
Nesting was introduced by Shneiderman and Johnson [9, 6] to strengthen the visualiza- tion of structure. Each rectangle that represents a non-leaf node is provided with a border to show that its children have the same parent. An example for a binary tree is shown in

figure 7(a). This method has some disadvantages. Extra screen-space is used, and fur- thermore, it gives rise to maze-like images, which can be puzzling for the viewer.

However, the second disadvantage can be remedied in a similar way as for the visual- ization of the nodes. We fill in the borders with grey-shades, based on a simple geometric model (figure 8). The width d l in pixels of a border of level l , with l = 1... n is given by:

where w is the width of the root level border, and f a factor that can be used to decrease the width for lower level borders. For the profile of the border we use a parabola:

where z l (r ) is the height of the profile for level l , r is the distance from the outside of the border for this level, and a and b are two coefficients that control the shape of the parabola.

Figure 7(b) shows the result for the binary tree. In this (exaggerated) example we used w = 8 , f = 1 , a = , 1 , and b = 16 , which gives a parabola with its top shifted to the interior. Figure 7(c) gives the profile of the frames for this example. Applications of a similar profile are shown in figure 9. This gives the following effects:

– nested borders appear as solid frames;

– the depth of each node in the tree is visualized directly via the height of the frame that surrounds it;

– neighbouring first level boundaries, such as the boundary between node 4 and 5, get an indent, because of the shift of the parabola;

– neighbouring second level boundaries, such as the boundary between node 2 and 3, have a smooth top;

– lower level boundaries have a sharp top.

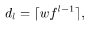
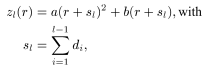
5 Discussion

We have presented two extensions to the standard treemaps. First, we have shown how rectangles can be forced to be more square. This gives rectangles that are easier to com-

pare, to point at, and that can represent sizes more accurately. Second, we have shown how frames can be used to improve the perception of structure. However, both methods have their limitations. With squarification, the relative ordering of siblings is lost and im- ages tend to be less regular, with less standard patterns, than standard treemaps. When structure of the tree is important and ordering in the data is not, the methods presented here will be very useful.

References

1. A. Bruggemann-Klein and D. Wood. Drawing trees nicely with tex. Electronic Publishing, 2(2):101–115, 1989.

2. S.K. Card, G.G. Robertson, and J.D. Mackinlay. The information visualizer, an information workspace. In Proc. of ACM CHI’91, Conference on Human Factors in Computing Systems, pages 181–188, 1991.

3. R. Chimera, K. Wolman, and B. Shneiderman. Evaluation of three interfaces for browsing hierarchical tables of contents. Technical Report Technical Report CAR-TR-539, CS-TR- 2620, University of Maryland, February 1991.

4. S.G. Eick. Visualization and interaction techniques. In CHI97 Tutorial notes on Information Visualization. ACM SIGCHI, March 1997.5. G.W. Furnas. Generalized fisheye views. In Proc. of ACM CHI’86, Conference on Human Factors in computing systems, pages 16–23, 1986.

6. B. Johnson and B. Shneiderman. Treemaps: a space-filling approach to the visualization of hierarchical information structures. In Proc. of the 2nd International IEEE Visualization Con- ference, pages 284–291, October 1991.

7. D.E. Knuth. Fundamental algorithms, art of computer programming, volume 1. Addison- Wesley, Reading, MA, 1973.

8. G.G. Robertson, J.D. Mackinlay, and S.K. Card. Cone trees: animated 3d visualizations of hierarchical information. In Proc. of ACM CHI’91, Conference on Human Factors in Com- puting Systems, pages 189–194, 1991.

9. B. Shneiderman. Tree visualization with tree-maps: a 2d space-filling approach. ACM Trans- actions on Graphics, 11(1):92–99, September 1992.

10. J.J. van Wijk and H. van de Wetering. Cushion treemaps - visualization of hierarchical infor- mation. In G. Wills and D. Keim, editors, Proceedings 1999 IEEE Symposium on Information Visualization (InfoVis’99), pages 73–78, October 1999.

11. M. Wattenberg. Map of the Market. http://smartmoney.com/marketmap/, Smart- Money.com, 1998.