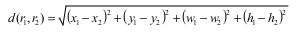Ordered and Quantum Treemaps:
Making Effective Use of 2D Space
to Display Hierarchies
Benjamin B. Bederson and Ben Shneiderman
University of Maryland
Source of information: http://hcil.cs.umd.edu/trs/2001-18/2001-18.pdf
Abstract
Treemaps, a space-filling method of visualizing large hierarchical data sets, are receiving
increasing attention. Several algorithms have been proposed to create more useful displays by
controlling the aspect ratios of the rectangles that make up a treemap. While these algorithms do
improve visibility of small items in a single layout, they introduce instability over time in the
display of dynamically changing data, fail to preserve order of the underlying data, and create
layouts that are difficult to visually search. In addition, continuous treemap algorithms are not
suitable for displaying quantum-sized objects within them, such as images.
This paper introduces several new treemap algorithms, which address these shortcomings. In
addition, we show a new application of these treemaps, using them to present groups of images.
The ordered treemap algorithms ensure that items near each other in the given order will be near
each other in the treemap layout. Using experimental evidence from Monte Carlo trials, we show
that compared to other layout algorithms ordered treemaps are more stable while maintaining
relatively favorable aspect ratios of the constituent rectangles. A second test set uses stock
market data. The quantum treemap algorithms modify the layout of the continuous treemap
algorithms to generate rectangles that are integral multiples of an input object size. The quantum
treemap algorithm has been applied to PhotoMesa, an application that supports browsing of large
numbers of images.
Introduction
Treemaps are a space-filling visualization method capable of representing large hierarchical
collections of quantitative data [9]. A treemap (Figure 1) works by dividing the display area into
a nested sequence of rectangles whose areas correspond to an attribute of the data set, effectively
combining aspects of a Venn diagram and a pie chart. Originally designed to visualize files on a
hard drive, treemaps have been applied to a wide variety of domains ranging from financial
analysis [7, 13] to sports reporting [5].
A key ingredient of a treemap is the algorithm used to create the nested rectangles that make up
the map. (We refer to this set of rectangles as the layout of the treemap.) The slice-and-dice
algorithm of the original treemap paper [9] uses parallel lines to divide a rectangle representing
an item into smaller rectangles representing its children. At each level of hierarchy the
orientation of the lines - vertical or horizontal - is switched. Though simple to implement, the
slice-and-dice layout often creates layouts that contain many rectangles with a high aspect ratio.
(In this paper we define the aspect ratio of a rectangle to mean the maximum of width/height and
height/width. Using this definition, the lower the aspect ratio of a rectangle, the more nearly
square it is; a square has an aspect ratio of 1, which is the lowest possible value.) Such long
skinny rectangles can be hard to see, select, compare in size, and label [3, 11]

Fig. 1 – A slice-and-dice layout. Shading indicates order, which is preserved.
Several alternative layout algorithms have recently been proposed to address these concerns. The
SmartMoney Map of the Market [13] is an example of the cluster treemap method described in
[14] which uses a simple recursive algorithm that reduces overall aspect ratios. Bruls, Huizing,
and van Wijk [3] introduced the squarified treemap, which uses a different algorithm to achieve
the same goal. Figure 2 shows examples of these two layouts.

Fig. 2 – Low aspect ratio layouts. Shading indicates order, which is not preserved.
These methods suffer from three drawbacks. First, changes in the data set can cause dramatic
discontinuous changes in the layouts produced by both cluster treemaps and squarified treemaps.
(By contrast, the output of the slice and dice algorithm varies continuously with the input data.)
These abrupt layout changes are readily apparent to the eye; below we also describe quantitative
measurements of the phenomenon. Large layout changes are undesirable for several reasons. If
the treemap data is updated on a second-by-second basis (e.g., in a stock portfolio monitor) then
frequent layout changes make it hard to track or select an individual item. Rapid layout changes
also cause an unattractive flickering that draws attention away from other aspects of the
visualization. Moreover, even occasional abrupt changes mean that it is hard to find items on the
treemap by memory, decreasing efficacy for long-term users.
The second shortcoming of cluster and squarified treemap layouts is that many data sets contain
ordering information that is helpful for seeing patterns or for locating particular objects in the
map. For instance, the bond data described in [6] is naturally ordered by date of maturity and
interest rate. In many other cases the given order is alphabetical. The original slice-and-dice
layout preserves the given ordering of the data, but cluster treemaps and squarified treemaps do
not. Another recent algorithm [12] enables control over the aspect ratios but does not guarantee
order. For someone to look for a particular item (assuming they are labeled), their eye has to
switch between horizontal and vertical scans many times, increasing cognitive load. A layout
that has a consistent visual pattern would be easier to search. We propose a measure, which we
call readability, that quantifies how easy it is to visually scan a treemap layout, and use it to
demonstrate the benefit of ordered layouts.
Another issue with treemap algorithms is what information is displayed in the generated
rectangles. In every current usage of treemaps to date, they are used to visualize a two-
dimensional dataset where typically, one dimension is mapped to the area of the rectangles (as
computed by the treemap algorithm), and the other dimension is mapped to the color of the
rectangle. Then, a label is placed in the rectangles which are large enough to accommodate
them, and the user can interact with the treemap to get more information about the objects
depicted by the rectangles. Surprisingly enough, there are not any published uses of treemaps
where other information is placed in the rectangles. We are interested in using treemaps to
display large numbers of image thumbnails, clustered by metadata.
There is a good reason why treemaps have not been used in this manner before. This is because
while treemaps guarantee that the area of each generated rectangle is proportional to an input
number, they do not make any promise about the aspect ratio of the rectangles. Some treemap
algorithms (such as squarified treemaps) do generate rectangles with better aspect ratios, but the specific aspect ratio is not guaranteed. While this is fine for general purpose visualizations, it is
not appropriate for laying out images because images have fixed aspect ratios, and they do not fit
well in rectangles with inappropriate aspect ratios.
In this paper, we introduce several new ordered treemap algorithms which address the three
limitations of existing treemap algorithms, and we also introduce a new family of quantum
treemap algorithms which address the use of treemaps to present fixed-size objects such as
images. 1
The ordered treemap algorithms change relatively smoothly under dynamic updates and roughly
preserve order, but also produce rectangles with low aspect ratios. One of them presents
rectangles in a predictable visually ordered style that should make human searching faster. We
discuss variations of the ordered treemap algorithms, each with slightly different properties.
We then report the results of Monte Carlo experiments comparing the ordered treemap
algorithms to squarified treemaps, cluster treemaps, and the slice-and-dice algorithm, using
natural metrics for smoothness of updates, overall aspect ratio, and readability. The results
suggest that ordered treemaps steer a middle ground, producing layouts with aspect ratios that
are far lower than slice-and-dice layouts, though not quite as low as cluster or squarified
treemaps; they update significantly more smoothly than clustered or squarified treemaps, though
not as smoothly as slice-and-dice layouts; one of the ordered treemaps offers layouts almost as
readable as slice-and-dice, which is significantly better than all of the others. Thus ordered
treemaps may be a good choice in situations where readability, usability and smooth updating all
are important concerns.
The quantum treemap algorithms are a family of treemap algorithms that extend the regular
continuous layout of other algorithms to generate rectangles whose sizes are multiples of a single
input dimension. This is useful for laying out images or other fixed-size objects (standard photos
(e.g. 4 by 6 inches) or document pages (e.g. 8.5 by 11 inches)) in the treemap rectangles. We
have used quantum treemaps to create a novel photo browser that shows many thumbnails of
images, clustered by metadata (where each cluster appears visually within a treemap-generated
rectangle). This application, called PhotoMesa, uses a zoomable user interface to enable simple
interactions to quickly find the desired photos, while offering the user control over the trade-off
between number and resolution of photos presented on the screen.
The Basic Ordered Treemap Algorithm
The key insight that leads to algorithms for ordered treemaps is that it is possible to create a
layout in which items that are next to each other in the given order are adjacent in the treemap.
Although such a layout does not follow the simple linear order of the slice-and-dice layout, it
provides useful cues for locating objects and turns out to provide constraints on the layout that
discourage large discontinuous changes with dynamic data.
We first discuss an algorithm for creating layouts that approximately preserves order. It follows a
simple recursive process, inspired in part by the idea of finding a two-dimensional analogue of
the well-known QuickSort algorithm.
The inputs are a rectangle R to be subdivided and a list of items that are ordered by an index and
have given areas. The first step is to choose a special item, the pivot, which is placed at the side
of R. In the second step, the remaining items in the list are assigned to three large rectangles that
make up the rest of the display area. Finally, the algorithm is then applied recursively to each of
these rectangles.
The algorithm has some minor variations, depending on how the pivot is chosen. We present
three pivot-selection strategies, but first explain the algorithm choosing the pivot with the largest
area. The motivation for this choice is that the largest item will be the most difficult to place, so
it should be done first. The algorithm, as illustrated in Fig. 3, can be described as follows:

Fig. 3 – The pivot configuration.
1. If the number of items is <= 4, lay them out in either a pivot, quad, or snake layout as
described in the next section, and pick the layout whose average aspect ratio is closest to 1.
Stop.
2. Let P, the pivot, be the item with the largest area in the list of items.
3. If the width of R is greater than or equal to the height, divide R into four rectangles, R 1 , R P ,
R 2 , and R 3 as shown in Fig. 2. (If the height is greater than the width, use the same basic
arrangement but flipped along the line y=x.)
4. Put P in the rectangle R P , whose exact dimensions and position will be determined in Step 5.
5. Divide the items in the list, other than P, into three lists, L 1 , L 2 , and L 3 , to be laid out in R 1 ,
R 2 , and R 3 . L 1 , L 2 and L 3 all may be empty lists. (Note that the contents of these three lists
completely determine the placement of the rectangles in Figure 3.) Let L 1 consist of all items
whose index is less than P in the ordering. Let L 2 and L 3 be such that all items in L 2 have an
index less than those in L 3 , and the aspect ratio of R P is as close to 1 as possible.
6. Recursively lay out L 1 , L 2 , and L 3 (if any are non-empty) in R 1 , R 2 , and R 3 according to this
algorithm by starting at step 1.
The alternate approaches to pivot selection are pivot-by-middle and pivot-by-split-size. Pivot-by-
middle selects the pivot to be the middle item of the list – that is, if the list has n items, the pivot
is item number n/2, rounded down. The motivation behind this choice is that it is likely to create
a balanced layout. In addition, because the choice of pivot does not depend on the size of the
items, the layouts created by this algorithm may not be as sensitive to changes in the data as
pivot by size.
Pivot-by-split-size selects the pivot that will split the list into approximately equal total areas.
With the sublists containing a similar area, we expect to get a balanced layout, eve n when the
items in one part of the list are a substantially different size than items in the other part of the list.
Figure 4 shows examples of the layouts created by these variations.

Fig. 4 – Pivot layouts. Shading indicates order, which is roughly preserved. The "P" indicates the first pivot rectangle in
each layout.
All pivot selection variations have the property that they create layouts that roughly preserve the
ordering of the index of the items, which will fall in a left-to-right and top-to-bottom direction in
the layout. The two algorithms are also reasonably efficient: pivot-by-size has performance
characteristics similar to QuickSort (order n log n average case and n 2 worst case) while pivot-
by-middle has order nlog n performance in the worst case.
Although the two algorithms produce layouts with relatively low aspect ratios (as described in
the following sections) they are not optimal in this regard. The stipulations in step 5 of the
algorithm avoid some but not all degenerate layouts with high aspect ratios, so we experimented
with post-processing strategies designed to improve the layout aspect ratio. For example we tried
adding a last step to the algorithm in which any rectangle that is divided by a segment parallel to
its longest side is changed so that it is divided by a segment parallel to its shortest side. Because
this step gave only a small improvement in layout aspect ratio while dramatically decreasing
layout stability, we did not include it in the final algorithm.
Stopping Conditions
Considering a few cases for laying out a small number of items can produce substantially better
total results when applied to the stopping condition of the ordered treemap algorithm.
The improvement comes from the realization tha t the layout of rectangles does not necessarily
give layouts with the best aspect ratios for all sets of 4 rectangles. In addition, it generates a
layout that is somewhat difficult to parse visually because the eye has to move in 3 directions to focus on the 4 rectangles (horizontally from R 1 to R P , vertically from R P to R 2 , and then
horizontally from R 2 to R 3 ).
The layout and visual readability can be improved by offering two alternative layouts to the
default “pivot” layout. The first alternative produces a “quad” of (2x2) rectangles. The second
produces a “snake” layout with all 4 rectangles layed out sequentially – either horizontally or
vertically. The snake layout can be equally well applied to 2, 3, or more rectangles. Figure 5
shows the result of laying out a sequence of 4 rectangles using the three stopping conditions.
Since no single layout strategy always gives the best result for all input data, the ordered treemap
algorithm computes layouts using all strategies at the stopping condition (pivot, quad, and snake)
and picks the best one. In practice, this strategy produces layouts with substantially squarer
aspect ratios. Running 100 randomized tests with 100 rectangles, and random area per rectangle,
ranging from 10 to 1000 produced an average aspect ratio of 3.9 with the original stopping
conditions, and 2.7 for the new stopping conditions.
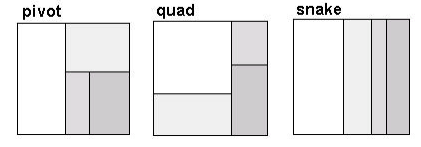
Fig. 5 – Result of applying different stopping conditions to same set of 4 rectangles
The Strip Treemap Algorithm
An alternative and simpler strategy gives surprisingly good results. The strip treemap algorithm
is a modification of the existing Squarified Treemap algorithm [3]. It works by processing input
rectangles in order, and laying them out in horizontal (or vertical) strips of varying thicknesses
(Figure 6). It is efficient in that it only looks at rectangles within the strip currently being
processed and produces a layout with significantly better readability than the basic ordered
treemap algorithm, and comparable aspect ratios and stability.
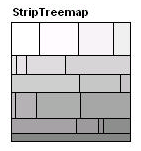
Fig. 6 – Strip treemap algorithm applied to 20 rectangles.
As with all treemap algorithms, the inputs are a rectangle R to be subdivided and a list of items
that are ordered by an index and have given areas. We describe here the algorithm for a horizontal layout, but it can easily be altered to produce vertically strips. We maintain a current
strip, and then for each rectangle, we check if adding the rectangle to the current strip will
increase or decrease the average aspect ratio of all the rectangles in the strip. If the average
aspect ratio decreases (or stays the same), the new rectangle is added. If it increases, a new strip
is started with the rectangle.
Note that the layout of any set of rectangles in a strip is deterministic. We calculate the area of
the set of rectangles, and from that and the width of the layout box, we compute the height of the
strip. Then given the height of the strip, we calculate the width of each rectangle so that it has
the appropriate area. The algorithm is as follows:
1. Scale the area of all the rectangles so that the total area of the input rectangles equals that
of the layout rectangle.
2. Create a new empty strip, the current strip.
3. Add the next rectangle to the current strip, recomputing the height of the strip based on
the area of all the rectangles within the strip, and then recomputing the width of each
rectangle.
4. If the average aspect ratio of the current strip has increased as a result of adding the
rectangle in step 3, remove the rectangle pus hing it back onto the list of rectangles to
process and go to step 2.
5. If all the rectangles have been processed, stop. Else, go to step 3.
The strip treemap complexity is understood as follows. For each rectangle, the algorithm
computes the average aspect ratio of the current strip. Each strip will be, on average, of length
equal to the square root of the total number of rectangles. Thus, the strip treemap algorithm runs
in O(sqrt(n)) time on average
As mentioned, this algorithm is similar to the squa rified treemap algorithm [3], but the squarified
treemap algorithm is more complex in two ways. Firstly, it sorts the input rectangles by size
which results in better aspect ratios, but (of course) loses the natural order of the rectangles.
Secondly, rather than creating all the strips horizontally, it creates either horizontal or vertical
strips in the remaining available space so as to produce the best aspect ratio. So really, strip
treemaps are a simplification of squarified treemaps – but a very important simplification as it
results in ordered layouts with aspect ratios that are only slightly worse.
The strip treemap algorithm also has some similarity to the space-filling treemap algorithm by
Eick et. al. [1]. They designed a strip layout algorithm that does maintain order. But, instead of
optimizing aspect ratios, they maintained near-constant strip heights to improve the ability of
people to compare the areas of each rectangle. Their algorithm works by deciding in advance the
number of strips, and then calculating the strip heights to be of constant height and laying the
rectangles out within those strips. Since the goal of their layout was to produce rectangles that
are easily comparable, they avoid splitting rectangles across strips (which could be necessary
since the strip heights are calculated independent of their content). They adjust the strip heights to accommodate moving the rectangles to one row or the other when they would otherwise be
split across strips.
Look Ahead for Strip Treemaps
The strip treemap algorithm as defined above works well, but frequently has a problem in laying
out the last strip. Since the decision to add a rectangle to a strip is made based only on the aspect
ratio of the strip being added to, it is possible to be stuck with a few left over rectangles that get
placed in a long skinny final strip.
This can be solved in a general way by adding lookahead to the layout. After a strip is
constructed with the approach described previously, the next strip is layed out to decide if any
rectangles would be better off moved from it to the current strip. The lookahead works as
follows.
The combined aspect ratio of the rectangles in the current strip and the aspect ratio of the
lookahead strip is compared to what would happen if the rectangles from the lookahead strip
were moved to the current strip. If the average aspect ratio is lower when moved to the current
strip, they are moved.
Adding lookahead to the strip treemap algorithm eliminates the final skinny strips that otherwise
can significantly increase the total average aspect ratio. Adding the lookahead function does not
change the complexity of the algorithm since you never have to process more than one other strip
which will have, on average, sqrt(n) rectangles. However, it clearly increases the runtime of any
implementation by at least a factor of 2
Metrics: Aspect Ratio, Change and Readability
In order to compare treemap algorithms we define three measures: 1) the average aspect ratio of
a treemap layout; 2) a layout distance change function which quantifies how much rectangles
move as data is updated; and 3) a readability function which is a measure of how easy it is to
visually scan a layout to find a particular item. The ideal would be to have a low average aspect
ratio, a low distance change as data is updated, and a high readability, though our experiments
suggest that there may be no treemap algorithm that is optimal by all three measures
We define the average aspect ratio of a treemap layout as the unweighted arithmetic average of
the aspect ratios of all leaf-node rectangles, thus the lowest average aspect ratio would be 1.0
which would mean that all the rectangles were perfect squares. This is a natural measure,
although certainly not the only possibility. One alternative would be a weighted average that
places greater emphasis on larger items, since they contribute more to the overall visual
impression. We choose an unweighted average since the chief problems with high aspect ratio
rectangles—poor visibility and awkward labeling—are at least as acute for small rectangles as
large ones.
The layout distance change function is a metric on the space of treemap layouts that allows us to
measure how much two layouts differ, and thus how quickly or slowly the layout produced by a
given algorithm changes in response to changes in the data. To define the distance change
function, we begin by defining a simple metric on the space of rectangles. Let a rectangle R be defined by a 4-tuple (x,y,w, h) where x and y are the coordinates of the upper left corner and w
and h are its width and height. We use the Euclidean metric on this space, i.e. if rectangles R 1
and R 2 are given by (x 1 , y 1 , w 1 , h 1 ) and (x 2 , y 2 , w 2 , h 2 ) respectively, then the distance between R 1
and R 2 is given by
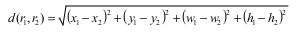
We use this metric since it takes into account the visual importance of the shape of a rectangle.
A change of 0 would mean that no rectangles moved at all, and the more the rectangles are
changed, the higher this metric will be. There are several plausible alternatives to this definition.
Two other natural metrics are the Hausdorff metric for compact sets in the plane or a Euclidean
metric based on the coordinates of the lower right corner instead of height and width. These
metrics differ from the one we chose by a small bounded factor, and hence would not lead to
significantly different results.
We then define the layout distance change function as the average distance between each pair of
corresponding rectangles in the layouts. We use an unweighted average for the same reasons as
we use an unweighted average for aspect ratios.
Finally, the readability metric assigns a numeric value to how easily it is likely to be for a person
to scan a layout to find a particular item. Scanning heavily relies on an ordered layout since
otherwise the entire layout would have to be scanned to find a particular item. We believe that
this kind of readability is correlated with the consistency and predictability of a layout.
Consistency allows the eye to follow a pattern quickly without having to jump. Predictability
allows the eye to jump ahead to the region the user thinks an item will appear.
We base our readability measure on the number of times that the motion of the reader's eye
changes direction as the treemap layout is scanned in order. To be precise, we consider the
sequence of vectors needed to move along the centers of the layout rectangles in order, and count
the number of angle changes between successive vectors that are greater than .1 radians (about 6
degrees). To normalize the measure, we divide this count by the total number of rectangles and
then subtract from 1. The resulting figure is equal to 1.0 in the most readable case, such as a
slice-and-dice layout, and close to zero for a layout in which the order has been shuffled. For a
hierarchical layout, we use an average of the readability of the leaf-node layouts, weighted by the
number of nodes each contains.
We considered other measures such as counting the average angular difference between
rectangles, but decided that once a rectangle sequence changed direction at all, it would force the
eye to stop and the amount it had to change direction was not as important as the fact that it
changed at all. Since the readability metric given above seems more subjective than the metrics
for layout change and aspect ratio, we also performed a user study to validate it.
Experimental design and results
To evaluate the performance of ordered treemap layout algorithms, we compared them to
squarified, cluster and slice-and-dice layouts with two experiments, and ran a user study. The
first experiment consisted of a sequence of Monte Carlo trials to simulate continuously updating
data. Our goal was to measure the average aspect ratio, average layout distance change, and readability produced by each of the algorithms. In the second experiment we measured the
average aspect ratio and readability produced by each of the algorithms for a static set of stock
market data. Finally, the user study validated the readability metric by having users search for
items in different treemap layouts.
Monte Carlo trials
We simulated the performance of the seven layout algorithms under a variety of conditions (slice
and dice treemaps, basic ordered treemaps with all three pivot selection strategies, strip treemaps,
clustered treemaps, and squarified treemaps). We performed experiments on three types of
hierarchies. The first hierarchy (“20x1”) was a collection of 20 items with one level of hierarchy.
The second ("100x1") was a collection of 100 items with one level of hierarchy. The third
(“8x3”) was a balanced tree with three levels of hierarchy and eight items at each level for a total
of 512 items.
For each experiment we ran 100 trials of 100 steps each. In each experiment we began with data
drawn from a log-normal distribution created by exponentiating a normal distribution with mean
0 and variance 1. This distribution is common in naturally occurring positive-valued data [8].
(Another common distribution, the Zipf distribution, has produced similar results in similar
experiments [10].) In each step of a trial the data was modified by multiplying each data item by
a random variable e x , where x was drawn from a normal distribution with variance 0.05 and
mean 0, thus creating a log-normal random walk. All layouts were created for a square with side
100. The results are shown in tables 1 through 3.

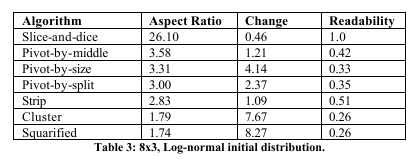
The results strongly suggest a tradeoff between low aspect ratios and smooth updates. As
expected, the slice-and-dice method produces layouts with high aspect ratios, but which change
very little as the data changes. The squarified and cluster treemaps are at the opposite end of the
spectrum, with low aspect ratios and large changes in layouts. The ordered and strip treemaps
fall in the middle of the spectrum. None produces the lowest aspect ratios, but they are a clear
improvement over the slice-and-dice method, with the pivot-by-split-size and strip treemap
algorithms producing slightly better aspect ratios. At the same time, they update more smoothly
than cluster or squarified treemaps, with the pivot-by-middle algorithm having a slight advantage
over the other pivot selection strategies, and the strip treemap doing especially well in the 8x3
case. Aside from the slice-and-dice layouts, strip treemap layouts are by far the most readable in
all cases.
Static stock market data
Our second set of experiments consisted of applying each of the seven algorithms to a set of 535
publicly traded companies used in the SmartMoney Map of the Market [13] with market
capitalization as the size attribute. For each algorithm we measured the aspect ratio of the layout
it produced. The results are shown in the first column of Table 4, and the layouts produced are
shown in Figures 14-20 at the end of this paper. (The gray scale indicates ordering within each
industry group that is the last level of hierarchy in this data set.) Note that although aspect ratios
are higher than in the statistical trials, partly due to outliers in the data set, the broad pattern of
results is similar.
User Study of Layout Readability
To validate the readability metric, we performed a user study to see how long it actually took
users to find specific rectangles layed out by different treemap algorithms. We compared the
squarified, basic ordered, and strip treemap algorithms by having subjects identify a specific
rectangle by clicking on the rectangle with the requested numerical ID. Each algorithm was applied to 100 rectangles with random sizes from a uniform distribution. Each subject did 10
tasks for each of the three algorithms. Each task consisted of a new random treemap where each
rectangle contained the number of that rectangle as specified in the input order to the algorithm
(Figure 7).
The study was run with a completely automated java application. The subjects were first asked
some demographic information. Then they were given training tasks followed by the
experimental tasks where the subjects were instructed to click on the rectangle containing the
target number at the bottom of the window. As the subject moved the mouse around, the
rectangle under the mouse was highlighted. The study was concluded with each subject rating
the three algorithms. So, there was a single independent variable (the treemap algorithm), and
two dependent variables (time and subjective preference).

Fig. 7 – Screen snapshot from the user study showing what users were presented with when told to click on a specific
rectangle. In this case, a basic ordered treemap was used and the user was told to click on rectangle #43.
We ran this experiment with 20 subjects. The subjects were 20% female and 80% male. They
were 55% aged 30-39 and 45% aged 20-29. 50% were students. 95% reported using a computer
20 or more hours per week while 5% reported using a computer 10-19 hours per week. The
subjects reported their primary major or field as being computer science (65%), HCI (15%),
informatics (5%), quality assurance (5%), marketing (5%), or unspecified (5%).
We analyzed the results of the experiment by running a single factor ANOVA for the two
dependent variables. The measured time (F 2,57 = 92.3) p < 0.0001 and subjective preference
(F 2,57 = 85.6) p < 0.0001 each had significant differences, so we performed a post-hoc analysis
using Tukey HSD. For the measured time, there was a significant difference between the
squarified treemap algorithm and the other two, but not between the basic ordered and strip
treemap algorithms. For subjective preference, there was a significant difference between all
three algorithms. Figure 8 shows the numeric results from the experiment.
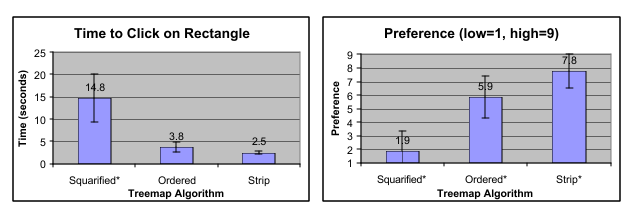
Fig. 8 – Results from user study validating readability metric. Error bars show standard deviation, and the algorithms
marked with an * are statistically different than the others.
The user study results do validate the readability metric. While the time measurement for the
strip and basic ordered treemap were not significantly different, the trend was in the same
direction as the readability metric (strip faster than basic ordered which is faster than squarified),
and the difference between the three algorithms for subjective preference was significant, and in
the same direction as the readability metric.
Algorithms for Quantum Treemaps
As mentioned in the introduction, we are also interested in using treemaps to present clusters of
visual information, such as images (Figure 9). We would like to be able to lay out images within
each rectangle generated by a treemap algorithm. That would enable us to create applications
that allow users to see an overview of a large set of information, but grouped in some meaningful
way. Some research in human-computer interaction shows that this kind of grouping of search
results based on meaningful categories, for instance, can help users understand those search
results [4].

Fig. 9 – PhotoMesa using quantum strip treemaps to group 556 images in 17 directories
Let us look at the problem of applying existing treemap algorithms to laying out fixed size
objects, such as images. For now, let us assume without loss of generality that the images are all
square (i.e., having an aspect ratio of 1). We will see later that this does not affect layout issues.
Given a list of groups of images that we want to lay out, the obvious input to the treemap
algorithm is the number of images in each group. The treemap algorithm will generate a list of
rectangles, and then we just have to decide how to fit each group of images in the corresponding
rectangle.
For each rectangle and group of images, the first step is to decide on the dimensions of a grid
with which to lay out the images in the rectangle. Given the aspect ratio of the rectangle, we
compute the number of rows and columns that best fit the images.
The resulting grid may have more spots than there are images, but will not have too many rows
or columns. This layout, however, is not guaranteed to fit in the rectangle. For example,
consider a rectangle that was computed to hold a single image. It will have an area of 1.0, but
could be long and skinny, perhaps with a width of 10.0 and a height of 0.1. The obvious solution
is to scale down the images just enough to fit in the bounds of the rectangle.
Herein lies the problem. Since each group of images has to fit in to a separate rectangle, each
group of images will have to potentially be scaled down. This will result in each group of
images being a different size. Furthermore, since the rectangles are arbitrarily sized and
positioned, and the images are scaled, the resulting groups of images will not align with each
other in a visually attractive way.
It is standard graphic design practice to align content in a way that makes it easy for the eye to
quickly scan different areas. If each group of images is a different size and they are not aligned,
this will make the resulting layout less attractive, and may make it slower for a user to quickly
scan. Figure 10 shows the result of laying out a simple sequence of images using the basic
ordered treemap and the quantum treemap algorithm we are about to describe to see the
difference in overall layout. Note how with the ordered treemap, group #4 consists of a single
image and is scaled much smaller than the other images. With the quantum treemap algorithm,
all images are the same size, and all images are aligned on a single grid across all the groups.
We have written an application called PhotoMesa, an image browser, which makes use of
quantum treemaps to layout groups of images. Figures 9 and 11 show screen snapshots of
PhotoMesa which may help to illuminate our interest in this kind of algorithm.
We designed PhotoMesa to support browsing of personal digital photos in a family environment.
Using metadata from the operating system (directory location, file change dates, and filenames),
PhotoMesa groups the photos and lays out the groups using the quantum strip treemap algorithm.
PhotoMesa uses a Zoomable User Interface (ZUI) to interact with the pho tos. Moving the mouse
highlights a region of photos, and clicking results in the view smoothly zooming into the
highlighted region. Right-clicking zooms out. In this way, users can easily get an overview of
1,000 photos at a time or more, and quickly zoom into photos of interest. Furthermore, this kind
of interaction naturally supports serendipitous photo finding. Since so many photos are visible,
users are likely to come across other photos of interest while looking for a specific one.
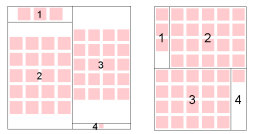
Fig. 10 – The result of laying out a sequence of 4
groups of elements (of size 3, 20, 20, 1) using Ordered
Treemap (left) and Quantum Treemap (right)
The goal of the quantum treemap algorithm is similar to other treemap algorithms, but instead of
generating rectangles of arbitrary aspect ratios, it generates rectangles with widths and heights
that are integer multiples of a given elemental size. In this manner, it always generates
rectangles in which a grid of elements of the same size can be layed out. Furthermore, all the
grids of elements will align perfectly with rows and columns of elements running across the
entire series of rectangles. It is this basic element size that can not be made any smaller that led
to the name of quantum treemaps.
Any treemap algorithm can be quantized, so really quantum treemaps (QTs) are a family of
algorithms that parallel the other treemap algorithms. QT’s input and output are similar to those
of other treemap algorithms, but instead of taking a list of areas as input, it takes an elemental
object dimension, and a list of numbers of objects. The output is a sequence of rectangles where
each rectangle is large enough (and possibly larger) to contain a grid of the number of objects
requested. The basic idea is to start the regular treemap algorithm and then as rectangles are generated, they are quantized. That is, their dimensions are expanded or shrunk so that each
dimension is an integral multiple of the input element size and the total area of the rectangle is no
less than that needed to layout a grid of the requested number of objects.
An unusual property of QTs is that the area of the generated rectangles is typically larger than
the object size multiplied by the number of objects to be layed out within that rectangle. The
reason for this is that many layouts will not precisely fill up a grid, but will leave some empty
cells in the last row. This is obviously true for numbers of objects that are prime (since they
have no divisors), but is also true for non-prime numbers where their factors do not generate
rectangles that have aspect ratios close to the aspect ratio of the rectangle generated by the
treemap algorithm.
While a generic quantization program could be written that would apply to the result of any
treemap algorithm, we instead have written custom quantum treemap variations of each ordered
treemap algorithm. This is because the custom ones are more efficient (in the amount of wasted
space) since the ongoing treemap algorithm can adapt to the error that is generated by quantized
rectangles.
We describe here a quantized (Q) version of strip treemaps (ST) and then summarize the issues
that affect quantization of other algorithms. The primary difference is in step 3 where the
rectangle dimensions are computed for the current strip. Instead of computing dimensions to
exactly match the requested area of each rectangle, the dimensions must be computed to be
integral multiples of the elemental input object size. With the original ST, the height of the strip
is calculated with (total-area-of-rectangles-in-strip / width-of-layout-box). But with QST the
height is calculated by taking the height as calc ulated by ST, and increasing it to the next highest
multiple of the input object height. Similarly, the width of each rectangle is grown or shrunk to
the next multiple of the input object width. It is shrunk if the resulting rectangle dimensions
would be large enough to accommodate the number of requested objects – otherwise, it is grown
as needed.
After this change, there is a remaining problem which is that the resulting treemap will have a
ragged right edge since some of the rectangles will have grown in width more than others, and
there can be differing numbers of rectangles on each row. Thus, there needs to be a concluding
evening step that evens out the ragged right edge. The simplest way to do this is to add enough
space to the width of the right-most rectangle in each strip so that the resulting width of the total
strip matches the width of the largest strip.
This simple approach to evening can result in some rectangles being expanded significantly with
the result that there will be a significant amount of empty space when the objects are laid out in
those rectangles. A simple solution is to distribute the extra space through all the rectangles in
the strip.
Quantizing a treemap algorithm does not change the complexity of the algorithm since it only
adds a constant cost to the processing of each rectangle. Quantizing other treemap algorithms
involves similar changes as to the ones we made to strip treemap, but the changes can sometimes
be a bit more subtle since the layouts are not as straightforward as they are for the strip layout.
We now look at a few issues that apply to quantization of any treemap algorithm.
Element Aspect Ratio Issues
QTs assume that all elements that will be layed out in the rectangles produced by QT are the
same aspect ratio, and that aspect ratio is an input parameter to QT. It turns out, however, that it
is not necessary to modify the internal structure of QT to accommodate the element’s aspect
ratio. Instead, the dimensions of the starting box can simply be stretched by the inverse of the
element aspect ratio. Simply put, laying out wide objects in a wide box is the same as laying out
thin objects in a thin box. Figure 11 shows ten articles from the ACM Interactions magazine,
each with a different aspect ratio.

Fig. 11 – PhotoMesa using strip treemaps to show the contents of ACM Interactions magazine. Note the aspect ratio of
the images is different than Figure 9.
Evening Ragged Edges
For QST, the job of evening the right ragged edge was straightforward since all the rectangles
are organized in strips and space could be readily distributed among the rectangles in each strip.
For other treemap algorithms with more complex layouts, handling ragged edges is a bit more
subtle. Since the rectangles are not laid out in strips, it is harder to spread extra space among
multiple rectangles. It requires working with the area as a whole, and evening the right-most and
bottom-most edge.
Growing Horizontally or Vertically
In the description of QST, we always grew the height of each rectangle, and then changed the
width of the rectangle as needed. However, more generally, there is a basic question of which
dimension to grow each rectangle. The simple answer is just to grow in the direction that results
in a rectangle that most closely matches the aspect ratio of the original rectangle. However, for
certain treemap algorithms, it may make more sense to grow in one direction than another. As
we saw for strip treemaps, for example, it makes most sense to have a constant height for each
strip, and so we grow the height of each rectangle and the adapt the width.
We have found that for the basic ordered treemap algorithm, it produces better layouts if it
always grows horizontally (or vertically for layout boxes that are oriented vertically). The issue
here is somewhat subtle, but is related to the evening of the rectangles. If (looking at Figure 3),
for example, rectangles in R 3 are made taller, than all of R 1 and R 2 will have to made taller as
well to match R 3 . If instead, the rectangles in R 3 are made wider, than only the other rectangles
in R 3 will need to be made wider, and the rectangles in R 1 and R 2 can be left alone.
Quantum Treemap Analysis
One of the basic characteristics of QTs is that they work better when there are mo re objects per
group. This is because it gives the algorithm more flexibility when computing rectangles. A
rectangle of, say, 1000 elements, can be arranged in quantified grids of many different sizes such
as (30x34), (31x33), (32x32) – each of which use the space quite efficiently, wasting only 2%
each. Rectangles containing smaller numbers of elements, however, do not offer as many
options, and often use space less efficiently. For example, a rectangle containing 5 elements can
be layed out in grids of (1x5), (2x3), (3x2), or (5x1). These four options do not give the
algorithm as much flexibility as the dozens of grid options afforded by the larger number of
elements. In addition, while the (1x5) layouts don’t waste any space, the (2x3) layouts each
waste 17% of the space (1 cell out of 6).
In order to assess the effectiveness of QTs, the strip treemap and ordered treemap were compared
to the quantized versions of the corresponding algorithm with a series of trials using random
input. Each algorithm was run 100 times generating 100 rectangles with the number of elements
in each rectangle being randomly generated with a uniform distribution. This was done for 5
different ranges of the number of elements per rectangle. For each test, the average aspect ratio
of all the rectangles was recorded as well as the space utilization, which was recorded as the
percentage of space not used to display elements (wasted space). The same random numbers
were used for each algorithm. Figures 12 and 13 show the results of these tests. Quantum
treemaps did better in terms of aspect ratio, and the non-quantized treemaps did better in terms of
wasted space.
However, the crucial visual advantage of QT is that it always produces layouts where elements
are the same size and are aligned on a single global grid. So, while understanding the
characteristics of QTs is important, for applications that need them, the importance of their
quantum characteristic will typically outweigh the others.

Fig. 12 – Average aspect ratio of all rectangles run on both ordered treemap algorithms and their quantized
counterparts with 100 rectangles with random numbers of elements per rectangle.
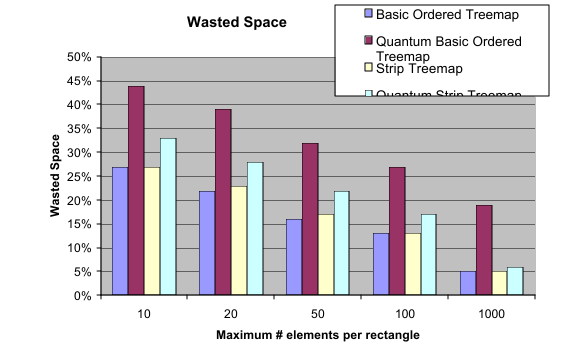
Fig. 13 – Average wasted space of all rectangles run on both ordered treemap algorithms and their
quantized counterparts with 100 rectangles with random numbers of elements per rectangle.
Conclusion and future directions
Treemaps are a popular visualization method for large hierarchical data sets. Although
researchers have recently created several algorithms that produce create treemap layouts with
low aspect ratios, these new algorithms have three drawbacks: they are unstable under updates to
the data, they scramble any natural order on the items being mapped, and they are difficult for
people to search them for a specific item.
We introduced several algorithms for ordered treemaps, which alleviate these problems by
creating layouts that preserve order and that update cleanly for dynamically changing data. One
of the algorithms offers substantially improved readability. Experimental results show that they
offer a useful compromise between the smooth updates of the slice-and-dice method and the low
aspect ratios of cluster treemaps and squarified treemaps.
There are several directions for future research. First, there is doubtless room to optimize the
ordered treemap algorithms discussed in this paper, especially to improve the overall aspect
ratios they produce. It would also be useful to optimize the algorithms used by cluster treemaps
and squarified treemaps to improve stability under dynamic updates. Another practical area to
explore would be mixing different algorithms to combine their strengths: for instance, using a
stable algorithm to lay out high-level nodes and an order-preserving algorithm to lay out leaf
nodes might provide a useful combination of global stability and local readability. More
speculatively, since experimental results suggest a tradeoff between aspect ratios and smoothness
of layout changes, it would be worthwhile to look for a mathematical theorem that makes this
tradeoff precise. It might also be fruitful to explore variants of treemap layouts that can update
smoothly by using past layouts as a guide to current ones, or by using tiles that can have
nonrectangular shapes [2].
More ambitious goals include accommodation of trees with millions of nodes. Rapid ways of
aggregating data and drawing only visible features are necessary, especially to handle continuous
updating. This is desirable for monitoring corporate computer networks with thousands of hard
drives, stock market trading with millions of transactions, and oil production from thousands of
wells and pumps.
Another challenge is to show more than two attribute values for each leaf node. Relationships
might be shown by animation (e.g. blinking), connected lines, textures, sounds, or other
perceptual methods.

Fig. 14 – Stock portfolio with slice-and-dice layout.

Fig. 15 – Stock portfolio with pivot-by-middle layout.

Fig. 16 – Stock portfolio with pivot-by-size layout.

Fig. 17 – Pivot by split

Fig. 18 – Stock portfolio with strip layout

Fig. 19 – Stock portfolio with cluster layout.

Fig. 20 – Stock portfolio with squarified layout.
Acknowledgements
This work has been supported in part by the DARPA Command Post of the Future program.
References
[1] Baker, M. J., & Eick, S. G. (1995). Space-Filling Software Visualization. Journal of Visual Languages and Computing, 6,
pp. 119-133.
[2] Bederson, B. B. (2001). Quantum Treemaps and Bubblemaps for a Zoomable Image Browser. In Proceedings of User
Interface and Software Technology (UIST 2001) ACM Press, (in press).
[3] Bruls, M., Huizing, K., & van Wijk, J. J. (2000). Squarified Treemaps. In Proceedings of Joint Eurographics and IEEE
TCVG Symposium on Visualization (TCVG 2000) IEEE Press, pp. 33-42.
[4] Hornof, A. J. (2001). Visual Search and Mouse Pointing in Labeled Versus Unlabeled Two-Dimensional Visual
Hierarchies. ACM Transactions on Computer-Human Interaction, (in press).
[5] Jin, L., & Banks, D. C. (1997). TennisViewer: A Browser for Competition Trees. IEEE Computer Graphics and
Applications, 17(4), pp. 63-65.
[6] Johnson, B. (1994). Treemaps: Visualizing Hierarchical and Categorical Data. Doctoral dissertation, University of
Maryland, College Park, MD.
[7] Jungmeister, W.-A. , & Turo, D. (1992). Adapting treemaps to stock portfolio visualization. Tech Report CS-TR-2996,
Computer Science Department, University of Maryland, College Park, MD.
[8] Sheldon, R. A. (1997). A First Course in Probability. Prentice Hall.
[9] Shneiderman, B. (1992). Tree Visualization With Treemaps: A 2-D Space-Filling Approach. ACM Transactions on
Graphics, 11(1), pp. 92-99.
[10] Shneiderman, B., & Wattenberg, M. (2001). Ordered Treemap Layouts. In Proceedings of IEEE Information
Visualization (InfoVis 2001) New York: IEEE, (in press).
[11] Turo, D., & Johnson, B. (1992). Improving the Visualization of Hierarchies With Treemaps: Design Issues and
Experimentation. (IEEE Visualization) IEEE, pp. 124-131.
[12] Vernier, F., & Nigay, L. (2000). Modifiable Treemaps Containing Variable-Shaped Units. In Proceedings of Extended
Abstracts of IEEE Information Visualization (InfoVis 2000) New York: IEEE, pp. 28-35. [13] Wattenberg, M. Map of the Market (1998). http://www.smartmoney.com/marketmap.
[14] Wattenberg, M. (1999). Visualizing the Stock Market. In Proceedings of Extended Abstracts of Human Factors in
Computing Systems (CHI 99) ACM Press, pp. 188-189.