Упорядоченные древовидные карты

Ben Shneiderman and Martin Wattenberg

University of Maryland and Columbia University

Перевод с английского: Серик М.А.

Источник: ftp://ftp.cs.umd.edu/pub/hcil/Reports-Abstracts-Bibliography/2001-06html/2001-06.htm

Аннотация

Древовидные карты, метод визуализцаии больших объемов иерархических данных путем заполнения пространства, получают все большее внимание. Множество алгоритмов было предложено для создания более наглядного визуального отображения, с помощью изменения коэффициентов соотношения сторон прямоугольников, составляющих карту. В то время как данные алгоритмы несомненно улучшают видимость небольших прямоугольников на карте, они также вносят нестабильность динамически изменямых данных с течением времени и не сохраняют упорядоченность данных лежащих в основе. В данное работе представлены упорядоченные древовидные карты, которые борются с этими двумя недостатками. Алгоритм, лежащий в основе упорядоченных древовидных карт гарантирует, что прямоугольники, расположенные рядом друг с другом в заданной наборе, будут рядом и на карте. Используя доказательства из эксперимента Монте-Карло, мы показываем, что упорядоченные древовидные карты являются более стабильными и в то же время сохраняют относительно низкие коэффициенты соотношения сторон прямоугольников. Второй тест использует данные фондового рынка.

1. Введение

Древовидные карты являются методом визуализации путем заполнения пространства карты, способные отображать большие наборы иерархических количественных данных [S92]. Древовидная карта (рис. 1) работает путем разделения пространства экрана на последовательность вложенных прямоугольников, размеры которых соответствуют атрибутам в наборе данных, эффективно сочитая в себе диаграмму Венна и круговую диаграмму. Первоначально разработанные для отображения файлов жесткого диска, древовидные карты применяются во множестве областей, начиная от финансового анализа [JT92, W98] и заканчивая спортивными обзорами[JB97].

Главным компонентом древовидной карты является алгоритм, применяемый для создания вложенных прямоугольников, составляющих карту. (Мы называем этот набор прямоугольников разметкой карты). Самый первый алгоритм «горизонталь-вертикаль» использует параллельные линии для разделения начального прямоугольника на меньшие дочерние прямоугольники. На каждом уровне иерархии орентация линий, вертикальная или горизонтальная, изменяется. Несмотря на простоту реализации, алгоритм «горизонталь-вертикаль» очень часто приводит к разметке, которая содержит множество прямоугольников с высоким коэффициентом соотношения сторон. Такие длинные, вытянутые прямоугольники может быть сложно заметить, выбрать, сравнить размеры и добавить аннотации. [TJ92, BHW00]

Рис.1 – Разметка алгоритма «горизонатль-вертикаль». Тени характеризуют упорядоченность, которая сохранена.

Несколько альтернативных алгоритмов разметки были недавно предложены для борьбы с данными недостатками. Приложение "Smartmoney of the market" это пример кластерного алгоритма, описанного в [W99], который использует простой рекурсивный алгоритм, уменьшающий общий коэффициент соотношения сторон. Bruls, huizing и Van Wijk [BHW00] представили квадратичные древовидные карты, которые используют другие алгоритмы для достижения этой цели. На рис. 2 показан пример этих двух разметок карты.

Рис.2 – Низкие коэффициенты соотношения сторон прямоугольников.Тени характеризуют упорядоченность, которая не сохранена.

Новые методы страдают от двух недостатков. Во-первых, изменение в наборе данных может привести к значитаельным перестроениям карты, сгенерированной кластерным и квадратичным алгоритмом. (В свою очередь, результат алгоритма «горизонталь-вертикаль» изменяется плавно при изменени в наборе данных.) Эти резкие изменения разметки карты видны человеческому глазу; дальше мы также опишем количественные измерения данного показателя. Большие изменения в разметки карты нежелательны по нескольким причинам. Если данные древовидной карты обновляются каждую секунду, частые изменения в портфеле ценных бумаг разметки приведут к тому, что данные будет сложно анализировать и выбирать отдельный прямоугольник. Быстрые изменения также приводят к непривлекательному морганию, которое отвлекает внимание пользователя от других аспектов визуализации. более того, даже если резкие изменеия разметки карты происходят не так часто, это значит, что данные на карте сложно найти по памяти, уменьшая эффективность для долгосрочных пользователей.

Другой недостаток разметки кластерных и квадратичных карт это то, что для многих наборов данных упорядоченность элементов важна для определения зависимостей или для размещения определенного прямоугольника на карте. Например, связанные данные, описанные в [J94] естественно упорядоченны по сроку оплаты и процентной ставке. Во многих других случаях упорядоченность идет по алфавиту. Алгоритм «горизонталь-вертикаль» сохраняет упорядоченность данных, но кластерные и древовидные карт – нет. Другой алгоритм [VN00], предложенный недавно, позволяет контролировать коэффициенты соотношения сторон прямоугольников, но не гарантирует йпорядоченность данных.

В этой работе представлены упорядоченные древовидные карты, которые создают разметку, изменяющуюся довольно плавно при динамическом изменении данных и которые примерно сохраняют упорядоченность элементов, и также приводят к прямоугольникам с низкими коэффициентами соотношения сторон. Мы рассматриваем два различных алгоритма создания упорядоченных древовидных карт, каждый с немного различными свойствами. (Демонстрация данных алгоритмов находится в инернете по адресу: http://www.columbia.edu/~mmw111/treemap.))

Затем мы приводим результаты экспериментов Монте-Карло, сравнивая упорядоченные древовидные карты с квадратичными и кластерными, а также алгоритмом «горизонталь-вертикаль», используя естественные метрики для плавности изменений и общего коэффициента соотношения сторон прямоугольников карты. Результаты показывают, что упорядоченные древовидные карты занимают промежуточное положение, приводя к разметки с коэффициентом соотношения сторон значительно более низким, чем для алгоритма «горизонталь-вертикаль», но не таким низким как для кластерных и квадратичных древовидных карт; они изменяются значительно более плавно, чем кластерные и квадратичные карты, но не так плавно, как для разметки «горизонталь-вертикаль». Поэтому, упорядоченные древовидные карты могут быть хорошим выбором в ситуациях, когда разборчивость, юзабилити и плавное изменение, все являются важными характеристиками.

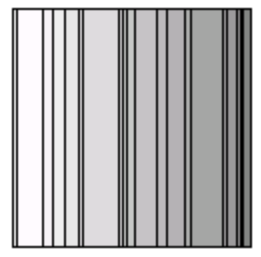
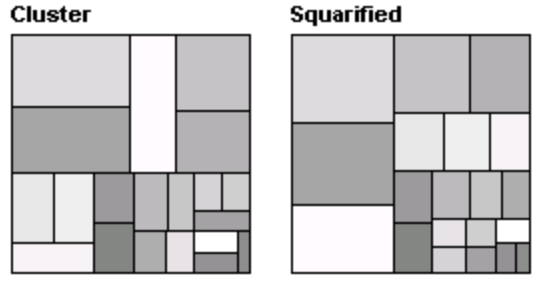
2. Алгоритмы для упорядоченных древовидных карт

Главной чертой, лежащей в основе упорядоченных древовидных карт является то, что возможно создать разметку, при которой элементы расположенным рядом друг с другом в заданном наборе находятся рядом и на карте. Несмотря на то, что такая разметка не строится по простому линейному принципу, как для алгоритма «горизрнталь-вертикаль», она обеспечивает достаточные ограничения для размещения прямоугольников таким образом, что при изменении данных карта перестраивается лишь немного.

Мы представляем два похожих алгоритма для создания разметов, которые приблизительно сохраняют упорядоченность элементов. Оба алгоритма следуют простому рекурсивному процессу, начиная от прямоугольника R, подлежащему разбиению. Входными данными является список элементов, упорядоченных по индексу и имеющие различную площадь. Определенный элемент (опорный) выбирается и размещается на начальном прямоугольнике R, как квадрат (коэффициент пропорциональности равен 1). Оставшиеся элементы размещаются в 3 больших прямоугольниках, образующих неиспользованное пространство прямоугольника R. Далее алгоритм рекурсивно применяется к каждому из этих 3 прямоугольников.

Для алгоритма «опорный элемент по размеру» в качестве опорного элемента выбирается элемент наибольшего размера, так как, обычно, чем больше элемент, тем его сложнее разместить, поэтому, лучше с него начать, когда вся карта свободна. Алгоритм, показанный на рис. 3, может быть описан так:

Рис.3 – Схема «опорного» элемента

1. Выбрать опорный элемент P, наибольший по размеру.

2. Если ширина начального прямоугольника R больше или равна высоте, разделить R на 4 прямоугольника R1, Rp, R2 и R3, как показано на рис. (Иначе, если ширина меньше высоты, поменять оси, y=x );

3. Расположить P в прямоугольнике Rp, точные размеры которого будут определены на шаге 4.

4. Разделить все элементы списка кроме P по 3 группам L1, L2 и L3, для добавления в прямоугольник R1, R2 и R3. L1 и L3 могут быть пустыми. Положим, что группа L1 состоит из элементов с индексом меньше чем P. Положим, что в группе L2 для всех элементов индекс меньше, чем в группе L3 и коэффициент пропорциональности P как можно ближе к 1.

5. Рекурсивно размещаем L1, L2 и L3 (если они не пустые) по прямоугольникам R1, R2, R3 в соответствии с алгоритмом.

Алгоритм «опорный в центре» практически идентичен рассмотренному выше, разница заключается в том, что в качестве опорного элемента выбирается не наибольший элемент, а просто центральный элемент (то есть, если последовательность состоит из n элементов в качестве опорного будет выбран элемент с индексом n/2). Причиной такого выбора является то, что создается сбалансированная разметка карты. Также, так как выбор опорного элемента не зависит от размера элементов, разметка получаемая при этом алгоритме будет не такой чувствительной к изменениям в данных, как при алгоритме «опорный элемент по размеру». На рис. 4 показаны примеры разметок, полученных данными двумя алгоритмами.

Рис.4 – Разметки для упорядоченных древовидных карт. Тени характеризуют упорядоченность, которая приблизительно сохранена.

Оба алгоритма имеют такое свойство, что они создают разметку приблизительно сохраняющую упорядоченность элементов, по правилу слева-направо и сверху-вниз. Оба алгоритма являются достаточно эффективными: для алгоритма «опорный элемент по размеру» производительность как и для быстрой сортировки (nlogn в среднем и n*n в худшем случае) и для алгоритма «опорный элемент в центре» – nlogn в худшем случае.

Несмотря на то, что обя алгоритма приводят к разметке с достаточно низкими коэффициентами соотношения сторон прямоугольников (как показано в следующих разделах), они не являются оптимальными касательно этого. Условие на шаге 4 алгоритма избегает некоторые, но не все разметки с высокими коэффициентами пропорциональности, поэтому мы экспериментировали со стратегиями пост-обработки для улучшения коэффициента соотношения сторон. Например, мы пробовали добавить последний шаг алгоритму на котором любой прямоугольник, который разделен сегментом, параллельным его длиной стороной заменяется на тот, который разделен сегментом, параллельным его короткой стороне. Так как данный шаг дает только небольшое улучшение разметки , в то время как значительно ухудшает стабильность карты, мы не включили его в финальный алгоритм.

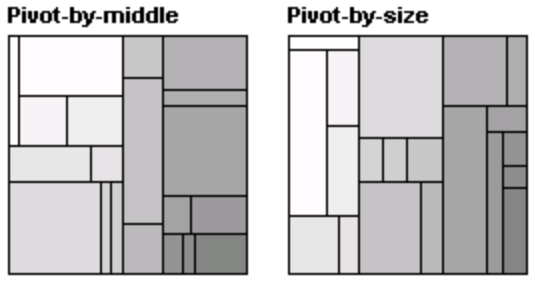
3. Метрики для разметки древовидных карт: коэффициент пропорциональности и изменения

Для сравнения алгоритмов древовидных карт мы вводим две метрики: средний коэффициент пропорциональности разметки карты и коэффициент изменения, который измеряет количественно проблемы визуализации из-заплохой разметки.

Выбираются «невзвешенные» средний коэффициент пропорциональности и динамического изменения, то есть прямоугольники с маленькой площадью влияют на данные коэффициенты, точно так же как и большие. Альтернативой может быть использование «взвешенных» коэффициентов, так как прямоугольники большего размера вносят больший вклад в общее визуальное представление. Однако проблема с вытянутыми прямоугольниками более характерна прямоугольникам меньшего размера и часто приходится ухудшать коэффициент пропорциональности больших прямоугольников в пользу маленьких. Использование «взвешенных» коэффициентов приводит к образованию маленьких, вытянутых прямоугольников.

Динамический коэффициент изменения характеризует насколько структура прямоугольников одной карты, отличается от другой. И, следовательно, чем данный коэффициент ниже, тем лучше: маленькие изменения в данных приводят лишь к небольшим перестроениям карты.

- x1, y1 – координаты верхнего левого угла 1-го прямоугольника;

- w1, h1 – координаты нижнего правого угла 1-го прямоугольника;

- x2, y2 – координаты верхнего левого угла 2-го прямоугольника;

- w2, h2 – координаты нижнего правого угла 2-го прямоугольника;

Есть несколько альтернатив этому определению, такик как метрика Hausdorff или Евклидова метрика, базируемая на координатах нижнего правого угла вместо ширины и высоты. Эти метрики отличаются лишь немного от той, которую мы выбрали и, следовательно, приведут к примерно таким же результатам.

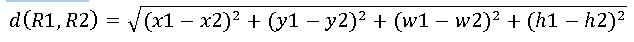
5. Выводы и направления для дальнейшей работы

Древовидные карты являются популярным методом визуализации больших объемов иерархических данных. Несмотря на то, что исследователи недавно предложили несколько алгоритмов, которые создают чистые, разборчивые разметки карты с низким коэфффициентом соотношения сторон, у новых алгоритмов есть два недостатка: они нестабильны при изменениях в данных и они не сохраняют естественную упорядоченность элементов.

Мы представили упорядоченные древовидные карты, которые борются с этими проблемами путем создания разметки, которая приблизительно сохраняет упорядоченность элементов и обновляется плавно при изменениях в данных. Экспериментальные результаты говорят, что упорядоченный древовидные карты представляют достойный компромисс между плавным обновлением алгоритма «горизонталь-вертикаль» и низким коэффициентом соотношения сторон прямоугольников кластерных и квадратичных карт.

Рис.5 - Портфель ценных бумаг, алгоритм «горизонталь-вертикаль».

Рис.6 - Портфель ценных бумаг, алгоритм «опорный элемент по центру».

Рис.7 - Портфель ценных бумаг, алгоритм «опорный элемент по размеру».

Рис.8 - Портфель ценных бумаг, кластерный алгоритм.

Рис.9 - Портфель ценных бумаг, квадратичный алгоритм.

Благодарности:

Спасибо Ben Bederson за вдумчивые предложения по работе.

6. Ссылки

[BHW00] Bruls, D.M., C. Huizing, J.J. van Wijk.

“Squarified Treemaps”. In: W. de Leeuw, R. van Liere (eds.), Data Visualization 2000, Proceedings of the joint Eurographics and IEEE TCVG Symposium on Visualization, 2000, pp. 33-42.

[JB97] Jin, L. and Banks, D.C. “TennisViewer: A Browser for Competition Trees.” IEEE Computer Graphics and Applications, July/August, pp. 63-65, 1997.

[JS91] Johnson, B. and and Shneiderman, B. “Tree-maps: A Space-filling Approach to the Visualization of Hierarchical Information Structures.” Proceedings of the IEEE Visualization ’91, pp. 284-291, October 1991.

[J94] Johnson, B. “Treemaps: Visualizing Hierarchical and Categorical Data” Unpublished PhD dissertation, Dept. of Computer Science, University of Maryland, College Park, MD (UMI-94-25057), 1994.

[JT92] Jungmeister, W-A. and Turo, D. “Adapting Treemaps to Stock Portfolio Visualization,” University of Maryland Technical Report CS-TR-2996, 1992. Available at http://www.cs.umd.edu/hcil/pubs/tech-reports.shtml

[R97] Sheldon, R. A First Course in Probability, Prentice Hall 1997.

[S92] Shneiderman, B. “Tree Visualization with Tree-Maps: 2-d Space-filling Approach.” ACM Transactions on Graphics, 11(1), pp. 92-99, 1992.

[TJ92] Turo, D. and Johnson. B. “Improving the Visualization of Hierarchies with Treemaps: Design Issues and Experimentation.” Proceedings of the IEEE Visualization 92, pp. 124-131, October 1992.

[VN00] Vernier, F. and Nigay, L. “Modifiable Treemaps Containing Variable-Shaped Units”, Extended Abstracts of the IEEE Information Visualization 2000. Available at

http://iihm.imag.fr/publs/2000/Visu2K_Vernier.pdf

[W98] Wattenberg, M. “Map of the Market. “SmartMoney.com, http://smartmoney.com/marketmap, 1998.

[W99] Wattenberg, M. “Visualizing the Stock Market,” Proceedings of ACM CHI 99, Extended Abstracts, pp.188-189, 1999.