Нейронная сеть на графическом процессоре

Авторы: Билл Конан, Кевин Гай

Источник: http://www.codeproject.com/KB/graphics/GPUNN.aspx

Перевод с английского: Шатохин Н.А.

Введение

Искусственные нейронные сети являются методом обработки информации, который был заимствован у биологической нервной системы, такой как мозг. Они состоят из большого числа тесно взаимосвязанных вычислительных элементов (нейронов), работающих в унисон, чтобы решать конкретные проблемы. Нейронные сети широко используются в классификации сигналов, таких как почерк, голос, и распознавании образов. Нейронные сети могут также использоваться в компьютерных играх. Это дает игре способность адаптивно обучаться поведению игрока. Эта техника используется в гоночных играх, поэтому противник, контролируемый компьютером способен обучаться стилю вождения игрока.

Нейронная сеть требует значительного числа векторных и матричных операций для получения результата, поэтому весьма удобно использовать для ее реализации в параллельную модель программирования и исполнять на графических процессорах (GPU). Нашей целью является использование и раскрытие потенциала графических процессоров для повышения производительности нейронной сети, решающей задачи распознавания рукописного текста.

Этот проект изначально был нашей курсовой работой по графической архитектуре. Мы запустили на GPU ту же нейронную сеть, которую Майк О'Нил описал в своей блестящей статье "Нейронные сети для распознавания рукописных цифр".

О нейронных сетях

Нейронные сети состоят из двух основных видов элементов: нейронов и связей. Нейроны соединяются друг с другом связями, формируя сеть. Это упрощенная теоретическая модель человеческого мозга.

Нейронные сети часто имеют несколько слоев; нейроны определенного слоя определенным образом соединяются с нейронами следующего уровення. Каждое соединение между ними имеет собственный вес. В начале, входные данные подаются на нейроны первого слоя, затем, вычисляя взвешенные суммы всех нейронов первого слоя, мы можем получить значения нейронов второго слоя и так далее. Наконец, мы можем достичь последнего слоя, который является выходом.

Весь секрет нейронной сети в значениях ее весовых коэффициентов. Правильные значения делают ее совершенной. Тем не менее, в начале, мы не знаем этих значений. Сначала мы должны обучить нашу сеть, подавая образцы на входы и сравнивая результаты с желаемыми. Некоторые алгоритмы принимают на входе значения ошибок и подстраивают весовые коэффициенты.

Рис. 1 - Сверточная нейронная сеть

Нейронная сеть, которую мы использовали, имела 5 слоев и являлась сверточной нейронной сетью. Такая сеть оказалась подходящей для распознавания рукописных цифр.

Первые три слоя нашей нейронной сети состоят из нескольких карт признаков. Каждый слой является сжатой версией предыдущего слоя. Наш вход это изображение цифры размером 29x29. Таким образом, мы имеем 29*29 = 841 нейронов в первом слое. Второй слой является сверточным с 6 картами признаков. Каждая карта является изображением размером 13x13 составленным из выходов первого слоя. Каждый пиксель/нейрон в карте является признаком участка изображения размером 5x5, поступающим с входного слоя. Таким образом, есть 13*13*6 = 1014 узлов/нейронов этого слоя, и (5*5+1 (смещение узла))*6 = 156 весов, 1014*(5*5+1) = 26364 соединений с первым слоем.

Третий слой также сверточный, но с картами признаков меньшими в 50 раз. Каждая карта имеет размер 5x5, и каждый пиксель в ней является признаком соответствующего участка размером 5x5 всех шести карт признаков предыдущего слоя. Таким образом, у нас есть 5*5*50 = 1250 нейронов в этом слое, (5*5+1)*6*50 = 7800 весов и 1250*26 = 32 500 соединений.

Четвертый слой представляет собой полносвязный слой со 100 нейронами. Так как он является полносвязным, каждый из 100 нейронов в слое связан со всеми 1250 нейронами в предыдущем слое. В нем 100 нейронов, 100*(1250+1) = 125100 весов и 100x1251 = 125100 соединений.

Пятый слой является выходным слоем. Этот слой также является полносвязным с 10 нейронами. Каждый из 10 нейронов в этом слое связан со всеми 100 нейронами предыдущего слоя. Здесь 10 нейронов, 10*(100+1) = 1010 весов и 10x101 = 1010 соединений.

Как вы можете видеть, эта нейронная сеть, хотя и структурно проста, но содержит огромное количество данных.

Предыдущие реализации на GPU

Быстрая нейросетевая библиотека (FANN) имеет очень простую реализацию нейронных сетей на GPU с помощью GLSL. Каждый нейрон представлен одним каналом цвета в пикселе текстуры. Эта сеть является очень специфической, значения нейронов лежат в пределах от 0 до 1 и имеют точность лишь 8 бит. Данная реализация использует преимущества аппаратного ускорения функций произведения для расчета выходов нейронов. Все расчеты ведутся на текстурных картах.

Данная реализация является простой и легкой, но притом ограниченной. Во-первых, в нашей нейронной сети, нам необходима 32-битная точность операций с плавающей точкой для каждого нейрона. Так как наша сеть состоит из пяти слоев, погрешность первого слоя может накапливаться и в итоге изменять конечные результаты. И поскольку очень важно, чтобы система распознавания рукописного ввода была достаточно чувствительной, чтобы обнаруживать небольшие различия между различными вводами, использование всего 8 бит для представления нейрона является неприемлемым. Во-вторых, обычно нейронные сети оперируют значениями в диапазоне от 0 до 1. Тем не менее, в нашей программе, нейронная сеть, специально предназначенная для распознавания рукописного ввода, имеет специальные функции активации, требующие значения в диапазоне от -1 до 1. Таким образом, если нейрон представлен одним значением цвета, как в библиотеке FANN, наши нейроны будут накапливать погрешность. Наконец, FANN использует скалярное произведение для вычисления нейронов, которое подходит для полносвязных нейронных сетей. В нашей реализации нейронной сети, нейроны частично связаны между собой. Вычисления в нашей нейронной сети включают в себя произведения больших векторов.

Наша реализация

Из-за всех неудобств GLSL, о которых упоминалось выше, мы в итоге выбрали CUDA. Причиной того, что нейронные сети очень удобны для вычислений на GPU, является то, что обучение и вычисление нейронной сети являются двумя отдельными процессами. Однажды правильно обученная сеть больше не потребует прав на запись при своем использовании. Поэтому нет проблемы синхронизации, которую необходимо решать. Более того, нейроны одного слоя сети полностью изолированы, поэтому вычисления значений нейронов могут достигнуть высокого уровня распараллеливания.

В нашем коде, веса первого слоя хранятся в виде массива, и входы копируются на устройство. Для каждого уровня сети есть функция CUDA осуществляющая вычисления значений нейронов этого уровня, так как параллелизм может быть достигнуто только в пределах одного слоя и связи между уровнями различны. Связи нейронной сети неявно определены в функции CUDA, содержащей уравнения для вычисления нейронов следующего уровня. Отсутствует четкая структура данных о связях. Это одно из главных отличий нашего кода и последовательной версии Майка.

Рис. 2 - Перенос сети на графический процессор

Например, значение каждого нейрона второго уровня является взвешенной суммой значений 25 нейронов первого уровня и одного смещения. Второй слой состоит из 6 карт признаков: каждая имеет размер 13x13. Мы назначим blockID для каждой карты и threadID для каждого нейрона карты. Каждая карта обрабатывается блоком и каждый ее пиксель вычисляется в потоке.

Это функция CUDA, которая вычисляет второй слой сети:

__global__ void executeFirstLayer
    (float *Layer1_Neurons_GPU,float *Layer1_Weights_GPU,float *Layer2_Neurons_GPU)
{
    int blockID=blockIdx.x;
    int pixelX=threadIdx.x;
    int pixelY=threadIdx.y;

    int kernelTemplate[25] = {
        0,  1,  2,  3,  4,
        29, 30, 31, 32, 33,
        58, 59, 60, 61, 62,
        87, 88, 89, 90, 91,
        116,117,118,119,120 };

    int weightBegin=blockID*26;
    int windowX=pixelX*2;
    int windowY=pixelY*2;

    float result=0;

    result+=Layer1_Weights_GPU[weightBegin];

    ++weightBegin;

    for(int i=0;i<25;++i)
    {
        result+=Layer1_Neurons_GPU
            [windowY*29+windowX+kernelTemplate[i]]*Layer1_Weights_GPU[weightBegin+i];
    }

    result=(1.7159*tanhf(0.66666667*result));

    Layer2_Neurons_GPU[13*13*blockID+pixelY*13+pixelX]=result;
} 

Все остальные слои вычисляются аналогичным образом, разница лишь в уравнениях расчета нейронов.

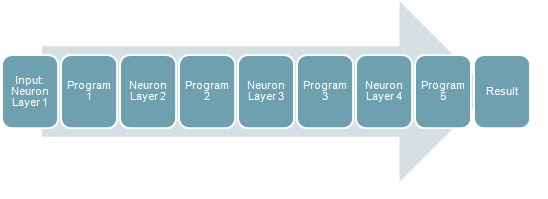
Рис. 3 - Шаги выполнения алгоритма

Основное приложение сначала копируется все входные данные на GPU, а затем по порядку вызывает каждую функцию CUDA и, наконец, возвращает ответ.

Пользовательский интерфейс является отдельной программой написанной на C#. Пользователь может мышью нарисовать цифру в поле ввода, затем программа сгенерирует изображение размером 29x29 и запустит ядро нейросетевой программы. Ядро, как описано выше, считает входное изображение и подаст его на вход нашей нейронной сети. Результат будет записан в файл, из которого затем прочитан пользовательским интерфейсом.

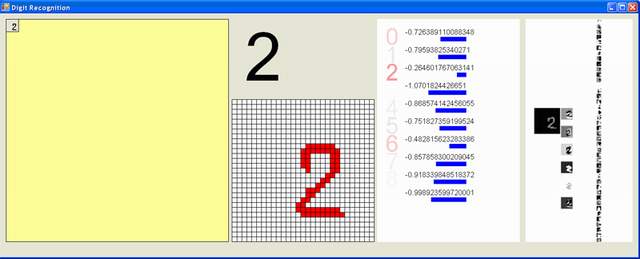
Рис. 4 - Окно приложения

Вот скриншот. После отрисовки цифры, мы получаем значения всех 10 нейронов последнего слоя сети. Индекс максимального значения нейрона будет наиболее вероятной цифрой. Мы раскрасили кандидатов красным цветом различной глубины в соответствии с их вероятностями.

Справа, пользовательский интерфейс будет выводить карты признаков первых трех слоев.

Обратите внимание, что C# под WindowsXP имеет проблему с разрешением. Мы протестировали нашу программу под 120dpi. Установка разрешения в 96 dpi может изменить входное изображение, так что точность серьезно пострадает.

Наша реализация не включает обучение. Мы используем код Майка, чтобы найти все веса и сохранить их в файлы.

Результат

Точность

Наша нейронная сеть может достичь 95% точности. В качестве базы данных для обучения сети мы использовали MNIST, содержащую 60000 примеров почерка разных людей. Доктор Лекун утверждает, что эта сеть может сходиться после примерно 25 эпохи обучения. Эта цифра была подтверждена нашими тестами. Мы достигли всего лишь около 1400 неправильных распознаваний образцов из 60000 входов.

Также отметим, что в коде Майка присутствует ошибка. Это исправленный код для инициализации второго слоя:

for ( fm=0; fm<50; ++fm)
{
  for ( ii=0; ii<5; ++ii )
  {
    for ( jj=0; jj<5; ++jj )
    {
      // iNumWeight = fm * 26;  // 26 is the number of weights per feature map
      iNumWeight = fm * 156;  // 156 is the number of weights per feature map
      NNNeuron& n = *( pLayer->m_Neurons[ jj + ii*5 + fm*25 ] );

      n.AddConnection( ULONG_MAX, iNumWeight++ );  // bias weight

      for ( kk=0; kk<25; ++kk )
      {
        // note: max val of index == 1013, corresponding to 1014 neurons in prev layer
        n.AddConnection(       2*jj + 26*ii + kernelTemplate2[kk], iNumWeight++ );
        n.AddConnection( 169 + 2*jj + 26*ii + kernelTemplate2[kk], iNumWeight++ );
        n.AddConnection( 338 + 2*jj + 26*ii + kernelTemplate2[kk], iNumWeight++ );
        n.AddConnection( 507 + 2*jj + 26*ii + kernelTemplate2[kk], iNumWeight++ );
        n.AddConnection( 676 + 2*jj + 26*ii + kernelTemplate2[kk], iNumWeight++ );
        n.AddConnection( 845 + 2*jj + 26*ii + kernelTemplate2[kk], iNumWeight++ );
      }
    }
  }
} 

Подрбности об этой ошибке вы можете прочесть по этой ссылке.

Наша реализация основана на правильной версии, однако там не слишком большая разница с точки зрения точности.

Производительность

Рис. 5 - Производительность

Основная причина использования GPU для вычисления нейронной сети заключается в увеличении скорости. Результат является впечатляющим по сравнению с последовательной реализацией. В таблице выше показано сравнение времени выполнения GPU версии, версии с эмуляцией и версии для процессора, принимающих на вход один и тот же образец. GPU версия ускоряется в 270 раз по сравнению с версией для CPU и 516,6 раза по сравнению с версии для эмулятора. Чтобы быть более точным, мы также включили время копирования данных во время исполнения версии для GPU.

Литература

1. Mike O'Neill. Neural Network for Recognition of Handwritten Digits. - 2006. - [Электронный ресурс]. Режим доступа: http://www.codeproject.com/KB/library/NeuralNetRecognition.aspx

Скачать пример (сборка потребует CUDA и 120 dpi) - 584.61 KB
Скачать исходный код GUI - 509.68 KB
Скачать ядро (нейронная сеть) - 2.78 KB