Распознавание речи на основе искусственных нейронных сетей

Автор: Ле Н. В.

Источник: http://w.moluch.ru/conf/tech/archive/3/712/

Библиографическое описание: Ле Н. В. Распознавание речи на основе искусственных нейронных сетей [Текст] / Н. В. Ле, Д. П. Панченко // Технические науки в России и за рубежом: материалы междунар. заоч. науч. конф. (г. Москва, май 2011 г.). / Под общ. ред. Г. Д. Ахметовой. — М.: Ваш полиграфический партнер, 2011. — С. 8-11.

Введение

Создание естественных для человека средств общения с компьютером является в настоящее время важнейшей задачей современной науки, при этом речевой ввод информации осуществляется наиболее удобным для пользователя способом. Разработка технологии распознавания речи ученые начали с освоения методики выделения информативных признаков, описывающих речевой сигнал. Затем приступили к решению задачи классификации речевых сигналов наборами информативных признаков.

Существуют следующие подходы к выделению информативных признаков, описывающих речевой сигнал:

• метод линейного предсказания;
• спектральный анализ.

Спектральный анализ отличается от линейного предсказания тем, что оценки среднего значения усредненного шума вычитаются из спектра, вычисленного по зашумленным данным.

Наиболее часто употребляются два подхода к классификации и распознаванию:

• мера близости параметров (такая функция называется метрикой);
• нейронные сети.

Второй подход не использует вспомогательных функций, но моделирует процесс распознавания в биологических системах. Этот подход представляется более перспективным в настоящее время.

В системах распознавания речи выделяются две основные подсистемы:

• подсистема предварительной обработки речевых сигналов;
• подсистема классификации речевых сигналов.

На рис. 1 показана схема предварительной обработки речевых сигналов. В настоящей работе представлены модель распознавания речи на основе искусственных нейронных сетей.

Рис. 1 - Схема предварительной обработки речевых сигналов

Модель распознавания речи на основе искусственных нейронных сетей

Пусть речевой сигнал как входные данные нейронной сети. После обработки звуковых данных получен массив сегментов сигналов. Каждый сегмент соответствует набору чисел, характеризующих амплитудные спектры сигнала. Для подготовки к вычислению для сигнала выхода нейронной сети необходимо записать все наборы чисел в таблицу, строка которой – это набор чисел каждого кадра.

Таблица 1 – Описание набора признаков речевого сигнала

Кадр	1-ое значение	2-ое значение	…	I-ое значение
1-ый кадр			…
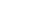
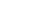
2-ый кадр			…
…	…	…	…	…
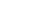
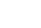
N-ый кадр			…

I – Количество значений одного набора чисел
N – Количество наборов чисел (кадр сигнала после нарезки)

Количество входных и выходных нейронов известно. Каждый из входных нейронов соответствует одному набору чисел. А на выходном слое только один нейрон, выход которого соответствует желаемому значению распознавания сигнала.

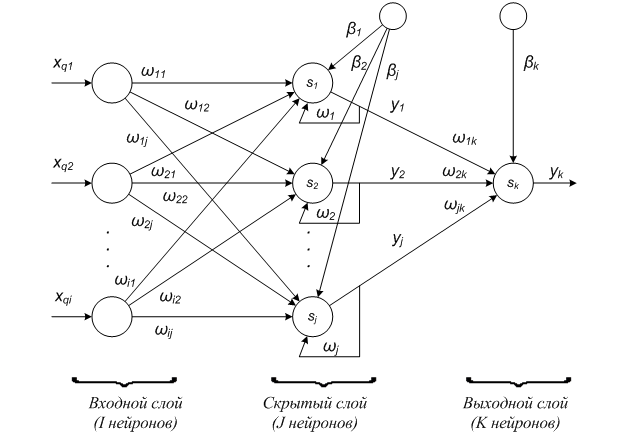
Рис. 2 – Структура нейронной сети с одной обратной связью

Где – i–ое входное значение q–го набора чисел;
– выход j–го нейрона слоя;
– весовой коэффициент связи, соединяющей i–ый нейрон с j–ым нейроном;
– весовой коэффициент обратной связи j–го нейрона;
– смещение j–го нейрона слоя.

Для вычисления выхода нейронной сети необходимо выполнить следующие последовательные шаги:

Шаг 1: Инициировать все контексты всех нейронов скрытого слоя.

Шаг 2: Подать первый набор чисел на вход нейронной сети . Вычислить для него выходы скрытого слоя.

где f(x) – нелинейная активационная функция .

Шаг 3: Если текущий набор чисел не является последним, то переход на шаг 5, иначе переход на шаг 4.

Шаг 4: Записать выходы нейронов скрытого слоя на контексты . Переход к шагу 2 для следующего набора чисел.

Шаг 5: Вычислить выход нейрона выходного слоя.

Рассмотрим задачу, которая состоит в распознавании чисел от 0 до 9. Для распознавания одного числа нужно построить собственную нейронную сеть. И так должно построить 10 нейронных сетей. Надиктована база из 250 слов (числа от 0 до 9) с различными вариациями произношения. База случайным образом разделялась на две равные части – обучающую и тестирующую выборки. При обучении нейронной сети распознаванию одного числа, например 5, желаемый выход этой нейронной сети должен быть единицей для обучающей выборки с числом 5, а остальные – нулю.

Обучение нейронной сети осуществляется путем последовательного предъявления обучающей выборки, с одновременной подстройкой весов в соответствии с определенной процедурой, пока ошибка настройки по всему множеству не достигнет приемлемого низкого уровня. Функции ошибки в системе будет вычисляться по следующей формуле:

где N – количество обучающих выборок, обработанных нейронной сетью примеров;
y – реальный выход нейронной сети;
d – желаемый (идеальный) выход нейронной сети.

Для каждого слова из тестовой выборки реальные выходы вычисляются 10 нейронными сетями распознавания разных чисел. Нейронная сеть, которая имеет максимальное выходное значение, и является нейронной сетью распознавания данного слова. И слово, распознанное нейронной сетью, является результатом распознания. Применение генетических алгоритмов для обучения нейронных сетей

Алгоритм обучения нейронной сети: необходимо произвести итерационную подстройку матрицы весов, постепенно уменьшая ошибку в векторах на выходе. Для обучения данной нейронной сети не может использоваться алгоритм с обратным распространением ошибки и его аналоги. Впервые в 1989 году Дэвид Монтана и Лоуренс Дэвис использовали генетические алгоритмы в качестве средства подстройки весов скрытых и выходных слоев для фиксированного набора связей.

Рассмотрим как используются генетические алгоритмы для подстройки весов скрытых и выходных слоев. Каждая хромосома (нейронная сеть) представляет собой вектор из весовых коэффициентов. Хромосома состоит из генов , которые могут иметь числовые значения. Приспособленность соответствует функции ошибки E.

Популяцией называют набор хромосом (решений). Эволюция популяций – это чередование поколений, в которых хромосомы изменяют свои признаки, чтобы каждая новая популяция наилучшим способом приспосабливалась к внешней среде.

Для генерации новых популяций к начальной популяции применяются основные генетические операторы:

• Оператор селекции осуществляет отбор хромосом в соответствии со значениями их функции приспособленности.
• Оператор скрещивания определяет передачу признаков родителей потомкам.
• Оператор мутации предназначен для того, чтобы поддерживать разнообразие особей популяции.
• Оператор инверсии заключается в том, что хромосома делится на две части, и затем они меняются местами.

Теперь, зная как интерпретировать значения генов, перейдем к описанию функционирования генетического алгоритма. Рассмотрим схему функционирования генетического алгоритма в его классическом варианте.

Шаг 1: Инициировать начальный момент времени t=0. Случайным образом сформировать начальную популяцию, состоящую из особей.

Шаг 2: Вычислить приспособленность каждой особи и популяции в целом. Значение этой функции определяет, насколько хорошо подходит особь, описанная данной хромосомой, для решения задачи.

Шаг 3: Выбрать одну особь из популяции.

Шаг 4: С определенной вероятностью скрещивания выбрать вторую особь из популяции и произвести оператор скрещивания над двумя хромосомами.

Шаг 5: С определенной вероятностью мутации выполнить оператор мутации над новой хромосомой.

Шаг 6: С определенной вероятностью инверсии выполнить оператор инверсии над новой хромосомой.

Шаг 7: Поместить полученную хромосому в новую популяцию.

Шаг 8: Если выполнилось условие останова, то завершить работу, иначе увеличить номер текущей эпохи t=t+1и переход на шаг 3.

Наибольшую роль в успешном функционировании алгоритма играет этап отбора родительских хромосом на шагах 3 и 4. Другой важный момент – определение критериев остановки.

Заключение

В результате проделанной работы предложена модель распознавания речи на основе искусственных нейронных сетей. Так же в настоящий момент разрабатывается подход обучения нейронной сети с применением генетического алгоритма. Данный подход будет реализован в системе распознавания чисел. Подходит к реализации системы распознавания отдельных голосовых команд. Также планируется разработать системы автоматического распознавания ключевых слов из потока речи, которые связаны с обработкой телефонных вызовов или сферой безопасности.

Литература

1. Компьютерное распознавание и порождение речи. [Электронный ресурс]. – Режим доступа: http://speech-text.narod.ru/chap3.html
2. Маркова, В.А. Сети Джордана и Элмана. [Электронный ресурс]. – Режим доступа: http://i-intellect.ru/articles-of-neural-networks/jordans-and-elmans-networks.html
3. Стариков, А. Генетические алгоритмы – математический аппарат. [Электронный ресурс]. – Режим доступа: http://www.basegroup.ru/library/optimization/ga_math/