

Вступ
В даний час швидко розвивається новий напрямок в теорії та практиці штучного інтелекту - еволюційні обчислення. Цей термін зазвичай використовується для загального опису алгоритмів пошуку, оптимізації або навчання заснованих на деяких формалізованих принципах природного еволюційного відбору. Особливості ідей еволюції і самоорганізації полягають в тому, що вони знаходять підтвердження не тільки для біологічних систем розвиваються багато мільярдів років. Ці ідеї в даний час з успіхом використовуються при розробці багатьох технічних і медичних програмних систем. Генетичні алгоритми були засновані в Мічиганському університеті американським дослідником Холландом і спочатку розроблені для задач оптимізації в якості досить ефективного механізму комбінаторного перебору варіантів рішення. На відміну від багатьох інших робіт, метою Холланда було не тільки рішення конкретних завдань, але дослідження явища адаптації в біологічних системах і застосування його в обчислювальних системах. При цьому потенційне рішення - особина представляється хромосомою - двійковим кодом. Популяція містить безліч особин. В процесі еволюції використовуються три основних генетичних оператора: репродукція, кросинговер і мутація. Також в 60-х роках у Німеччині Рехенберг заклав основи "еволюційних стратегій" при вирішенні задачі оптимізації речових параметрів у розрахунку ліній електропередачі. Це напрямок розвивався довгі роки незалежно і тут були отримані важливі фундаментальні результати. Фогель незалежно від інших дослідників заснував еволюційне програмування, де потенційне рішення представляється кінцевим автоматом. Основним генетичним оператором тут також є мутація, яка випадковим чином змінює таблицю переходів-виходів автомата. Трохи пізніше Коза в Массачусетському технологічному інституті США заклав основи генетичного програмування. Тут як особини виступала програма на LISP, яка представлялася деревоподібній структурою. На цих структурах були розроблені генетичні оператори кросинговеру і мутації. В даний час вказані напрями об'єднані в "еволюційні обчислення", які успішно застосовуються при вирішенні багатьох проблем. При цьому окремі напрями успішно взаємодіють за рахунок запозичення кращих рис один у одного.
Постановка задачі
Найбільш перспективний напрямок для вирішення завдань медичного прогнозування грунтується на інтелектуальному аналізі даних із застосуванням сучасного програмного забезпечення. На першому етапі якого необхідно визначити фактори ризику і оцінити їх інформативність. Як правило, відбір даних для аналізу виконується лікарем за наступним принципом: спочатку здійснюється виділення факторів ризику відносяться до певної патології і в основному за формальною принципом: обтяжений сімейний анамнез, перинатальні фактори, захворювання в анамнезі, несприятлива макросоціальних середа, соціально-гігієнічні фактори і т . д. Потім групи факторів ризику визначаються часом їх впливу, видом (біологічні, середовищні і т. д.) і кількістю впливаючих чинників. Наприклад, при аналізі даних, наданих різними лікарями для прогнозування тих чи інших захворювань в області гінекології можна зробити висновок, що перелік зібраних факторів, є відносно стабільним, причому однаковим для аналізу більшості гінекологічних проблем і дуже великим. У нього входять медичні та соціально-демографічні фактори. Слід зазначити, що в медичних завданнях, доводиться аналізувати велику кількість неоднакових за значимістю факторів ризику, які до того ж можуть бути взаємопов'язані, тому застосування статистичних методів у даному випадку неефективно. Тепер розглянемо цю задачу з математичної точки зору. Припустимо, існує набір факторів ризику S, що містить m прикладів (1.1). Кожен приклад, Si набору даних S складається з n визначальних параметрів Xi = (x1, x2, ..., xn) і параметра - результату Yi.


Таким чином, кожен i-й приклад набору даних S представлений набором значень факторів ризику Х і результату Y. При цьому чинники ризику X набору даних S можуть включати в себе як фактори, що містять корисну інформацію, так і фактори, частково або повністю неінформативні. Крім цього, інформативні чинники теж можуть містити шум. Необхідно виконати відбір значущих чинників і оцінити якість такого набору даних за критерієм оцінки E (X). Тоді завдання зводиться до знаходження такого вектора X, при якому досягається допустима точність класифікації при мінімальній кількості вхідних параметрів (1.3):

де є - допустима похибка, n-кількість факторів ризику, nmin - бажану кількість факторів ризику. Як критерій оцінювання можна використовувати формулу (1.4).

де М - кількість навчальних прикладів, F - отриманий результат, Y - бажаний результат.
Цілі та задачі
Метою даної роботи є отримати корисну інформацію з набору параметрів (факторів ризику) і підготувати дані для навчання аналітичної системи, призначеної прогнозувати втрату крові при пологах.
Загальні теоретичні відомості
ГА використовують принципи і термінологію, запозичені у біологічної науки - генетики. У ГА кожна особина представляє потенційне рішення деякої проблеми. У класичному ГА особина кодується рядком двійкових символів - хромосомою, кожен біт якої називається геном. Безліч особин - потенційних рішень становить популяцію. Пошук (суб) оптимального вирішення проблеми виконується в процесі еволюції популяції - послідовного перетворення одного кінцевого безлічі рішень в іншу за допомогою генетичних операторів репродукції, кроссинговера і мутації. ГА використовують такі механізми природної еволюції.
Перший принцип заснований на концепції виживання найсильніших і природного відбору за Дарвіном, який був сформульований ним в 1859 році в книзі «Походження видів шляхом природного відбору». Згідно Дарвіну особини, які краще здатні вирішувати задачі в своєму середовищі, виживають і більше розмножуються (репродукують). У генетичних алгоритмах кожна особина є рішення деякої проблеми. За аналогією з цим принципом особини з кращими значеннями цільової (фітнес) функції мають великі шанси вижити і репродукувати. Формалізація цього принципу дає оператор репродукції.
Другий принцип обумовлений тим фактом, що хромосома нащадка складається з частин отриманих з хромосом батьків. Цей принцип був відкритий в 1865 році Менделем. Його формалізація дає основу для оператора схрещування (кросинговера).
Третій принцип заснований на концепції мутації, відкритої в 1900 році де Вре. Спочатку цей термін використовувався для опису істотних (різких) змін властивостей нащадків і придбання ними властивостей, відсутніх у батьків. За аналогією з цим принципом генетичні алгоритми використовують подібний механізм для різкої зміни властивостей нащадків і тим самим, підвищують різноманіття (мінливість) особин в популяції (безлічі рішень).
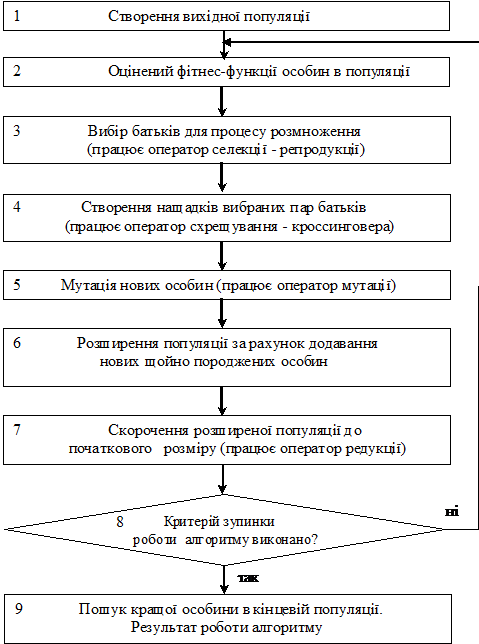
Ці три принципи складають ядро ЕВ. Використовуючи їх, популяція (безліч варіантів розв'язання проблеми) еволюціонує від покоління до покоління. Еволюцію штучної популяції - пошуку безлічі рішень деякої проблеми формально можна описати алгоритмом, який представлений на рис. 2.1. ГА бере безліч параметрів оптимізаційної проблеми і кодує їх послідовностями кінцевої довжини в деякому кінцевому алфавіті (в найпростішому випадку двійковий алфавіт «0» і «1»). Попередньо простий ГА випадковим чином генерує початкову популяцію стрінгів (хромосом). Потім алгоритм генерує наступне покоління (популяцію), за допомогою трьох основних генетичних операторів:
Оператор репродукції (ОР).
Оператор кроссинговера (ОК).
Оператор мутації (ОМ).
Генетичні оператори є математичної формалізацією наведених вище трьох основоположних принципів Дарвіна, Менделя і де Вре природної еволюції. ГА працює до тих пір, поки не буде виконано задану кількість поколінь (ітерацій) процесу еволюції або на деякій генерації буде отримано задану якість або внаслідок передчасної збіжності при попаданні в деякий локальний оптимум.
У кожному поколінні безліч штучних особин створюється з використанням старих і додаванням нових з гарними властивостями. Генетичні алгоритми - не просто випадковий пошук, вони ефективно використовують інформацію накопичену в процесі еволюції. На відміну від інших методів оптимізації ГА оптимізують різні області простору рішень одночасно і більш пристосовані до пошуку нових областей з найкращими значеннями цільової функції за рахунок об'єднання квазіоптимального рішень з різних популяцій.
Відбір факторів за допомогою ГА
На першому етапі необхідно визначиться з математичним апаратом для вирішення завдання прогнозування розвитку акушерських кровотеч. Для вирішення цього завдання можна використовувати нейронну мережу (НС) [2,3]. Для практики найважливішим є визначення ризику втрати крові при пологах більш ніж 0,5% від маси тіла, з метою вжиття відповідних заходів. У цьому випадку, по суті, виконується класифікація на два класи: кровотеча і допустимий. Для реалізації поставленого завдання в такій формі доцільно використовувати багатошарову НС прямого поширення. Далі за допомогою ГА визначається оптимальний набір вхідних параметрів. Після того як визначена і успішно навчена НС, виконується ГА, який подає різні комбінації факторів ризику на входи НС і потім виконується спроба навчити мережу при такій комбінації відібраних факторів ризику. Принцип реалізації кодування хромосоми представлений на рис. 2.2. Кожна хромосома представляє собою послідовність певної кількості бітів (визначається максимальною кількістю чинників ризику). Значення кожного біта дорівнює 1, якщо фактор з відповідним номером присутній в даному наборі, і нулю, якщо цей фактор відсутній. У пропонованому підході для виділення ознак використаний генетичний алгоритм, який має модифіковану схему реалізації стосовно до задачі багатокритеріальної оптимізації. У той час як більшість подібних методів, використовуваних для рішення таких задач, використовує єдиний, складовою оптимізується критерій [4]. Рішенням задачі в даному випадку є кілька недомініруемих підмножин ознак. Розроблено фітнес-функція (2.1), яка передбачає пошук рішення, що є оптимальним згідно з двома критеріями? враховується точність класифікації і кількість факторів ризику. До того ж дана фітнес-функція дозволяє задавати бажане співвідношення точності класифікації та кількості факторів ризику.

де Xi - кількість присутніх факторів ризику в i-й хромосомі, Xn - максимальна кількість факторів ризику, Ei - помилка навчання НС для i-ї хромосоми, En - помилка навчання НС при використанні максимальної кількості факторів, Q1 і Q2 - коефіцієнти, за допомогою яких регулюється співвідношення між точністю класифікації і числом факторів ризику. Рекомендується вибирати діапазон значень (2.2), і дотримуватися умови (2.3).



Генетичні оператори виконуються стандартні.
Найпростіший метод реалізації ОР - побудова колеса рулетки, в якій кожна хромосома має сектор, пропорційний її значенням ЦФ.
Простий оператор кросинговер із заданою вірогідністю Pc виконується в 3 етапи (рис.2.3):
1-й етап. Вибираються дві хромосоми (батьки) випадково з проміжної популяції, сформованої за допомогою оператора репродукції
2-й етап. Випадково вибирається точка схрещування - число k з діапазону [1,2 ... n-1], де n - довжина хромосоми (число біт у двійковому коді)
3-й етап. Дві нові хромосоми A ', B' (нащадки) формуються з A і B шляхом обміну підрядків після точки схрещування:

ОК виконується з заданою вірогідністю Pc (відібрані два батьки не обов'язково проводять нащадків).
Оператор мутації грає вторинну роль і його ймовірність зазвичай мала. Оператор мутації виконується в 2 етапи:
1-й етап. У хромосомі A (рис. 3) випадково вибирається k-а позиція (біт) мутації (1 <= k <= n).

2-й етап. Проводиться інверсія значення гена в k-й позиції. (рис 4.)

Висновок
Розглянуто і вирішено актуальне завдання відбору факторів ризику розвитку акушерський кровотеч для розробки медичної аналітичної системи прогнозування ризику патологічної втрати крові при пологах. Виконано математичну постановку задачі відбору інформативних даних. Розроблено фітнес-функція для еволюційного методу відбору інформативних даних. Надалі планується реалізація реальної КС для виконання поставленої задачі.
Література1. Скобцов Ю. О. Основи еволюційних обчислень / Скобцов Ю. О. – Донецьк: ДонНТУ, 2009. – 316 с.
2. Рутковская Д. Нейронные сети, генетические алгоритмы и нечеткие системы / Рутковская Д., Пилинский М., Рутковский Л. - М.: Горячая линия – Телеком, 2006. – 452 с.
3. Саймон Хайкин Нейронные сети: полный курс, 2-е издание. : Пер. с англ. – М. : Издательский дом «Вильямс», 2006. – 1104 с.
4. Васяева Т.А. Отбор факторов риска потери крови при родах / Т.А. Васяева, Д.Е. Иванов, И.В. Соков. // Інтелектуальні системи прийняття рішень і проблеми обчислювального інтелекту: Матеріали міжнародної наукової конференції. Том 1. - Херсон: ХНТУ, 2011. – 472 с.
5. Архангельский А.Я. Программирование в С++ Builder 6. – М.: ЗАО «Издательство БИНОМ», 2002г. – 1152с.