|
Cерія «Інформатика, кібернетика та обчислювальна техніка», 2009, №10, с. 17-20 Реализация параллельного алгоритма построения марковских моделейФельдман Л.П., Михайлова Т.В., Ролдугин А.В.Донецкий национальный технический университетAbstarctFeldman L., Michailova T., Roldugin A.V. Efficiency of parallel algorithm of construction of discrete Markov’s models. In the work there is presented a discreet Markov’s model algorithm, which allows fastening a Markov’s model’s computation. ВведениеСоздание и использование современных суперкомпьютерных систем стало в наше время одним из основных направлений в ведущих странах мира. Одной из основных проблем, возникающих при проектировании и эксплуатации параллельных и распределенных вычислительных систем (ВС) является выработка рекомендаций рационального использования ресурсов вычислительной среды. Одним из эффективных способов решения этой проблемы может быть использование результатов непрерывных [1,2,3] или дискретных аналитических моделей [4]. Дискретная модель кластера с совместным разделением дискового пространства [5] при использовании методов построения дискретных Марковских моделей [6] описана в [7]. Анализ кластерных систем с помощью этих моделей при большом количестве решаемых задач на ЭВМ требует больших временных затрат, так как количество состояний дискретной Марковской модели комбинаторно возрастает при увеличении количества задач. Для решения этой проблемы предложен параллельный алгоритм построения дискретной модели [7]. Сравним теоретическую трудоемкость этого алгоритма и характеристики распараллеливания с реальными. Данная статья является продолжением и развитием работ [7, 8]. Теоретическая оценка трудоемкости параллельного алгоритма расчета характеристик функционирования кластерной системыАлгоритм построения дискретной Марковской модели [7,8] состоит из двух частей: вычислений матрицы переходных вероятностей и вектора стационарных вероятностей. Теоретическая оценка трудоемкости алгоритма вычисления матрицы переходных вероятностей, учитывая, что tсл ≈ tумн, определяется как: 
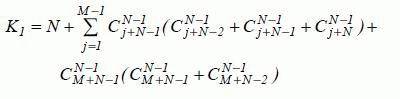
Для определения трудоемкости вычисления вектора стационарных вероятностей. Представим СЛАУ в виде 
где Возведение матрицы Р в степень Z потребует (1+log2Z) операций умножения матрицы. При последовательной реализации расчета вектора стационарных вероятностей общее количество вычислений определяется как 
Вычислительная сложность последовательного алгоритма построения дискретной Марковской модели кластера с общей памятью вычисляется как сумма (2) и (4) Отображение параллельного алгоритма Марковской модели на решетку процессоровПусть процессор имеет топологию-решетку процессорных элементов (ПЭ) p=n2. Каждый ПЭ может выполнить любую операцию за один такт; время обращения к запоминающему устройству ПЭ пренебрежительно мало по сравнению со временем выполнения операции. На каждом ПЭ с индексами i, j вычисляется один элемент матрицы переходных вероятностей pij. Алгоритм вычисления переходной вероятности между двумя произвольными состояниями приведен в [6]. Временная сложность вычисления одного элемента матрицы переходных вероятностей размерности L определяется как 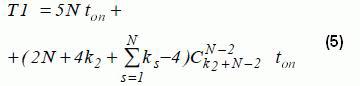
Число ненулевых элементов матрицы переходных вероятностей определяется величиной K1. В этом случае временная сложность параллельного алгоритма вычисления матрицы переходных вероятностей вычисляется следующим образом 
Временная сложность последовательного алгоритма определяется (1). Ускорение параллельного алгоритма вычисления матрицы переходных вероятностей на решетке процессоров, определяемое как отношение выражений (1) и (6) для различных значений количества обрабатываемых на кластере задач представлено на рис.1 для решетки процессоров p=64; при этом изменялась конфигурация кластера, т.е. увеличивалось количество устройств(серверов и/или дисков) в узлах. Эффективность параллельного алгоритма вычисления матрицы переходных вероятностей на решетке процессоров с увеличением количества решаемых задач М незначительно растет (рис.2.) и мало изменяется (в сотых долях) с ростом количества процессоров. 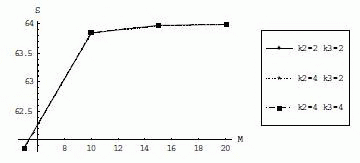
Эффективность параллельного алгоритма вычисления матрицы переходных вероятностей на решетке процессоров зависит от значений М и не зависит от значений k2, k3. Распараллелим вычисление вектора стационарных вероятностей на решетку процессоров размерности p=n2 с использованием блочного подхода методом Фокса [8,9]. Размер блоков матрицы переходных вероятностей Р равен 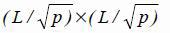

Временная сложность вычисления вектора стационарных вероятностей блочным методом Фокса определяется как 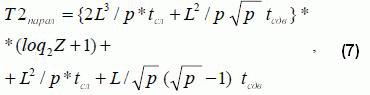
Порядок вычислений последовательного алгоритма - L3(1+log2Z). Ускорение и эффективность параллельного алгоритма вычисления вектора стационарных вероятностей на решетке процессоров представлены на рис.3, рис.4. 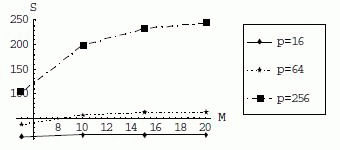
Временная сложность алгоритма построения модели Маркова определяется суммой (6) и (7). Ускорение параллельного алгоритма асимптотически приближается к количествупроцессоров (рис.5) и не зависит от количества устройств (серверов и/или дисков) в узлах кластера. Поэтому в формулах оценки трудоемкости алгоритма вычисления матрицы переходных вероятностей можно отброситьслагаемые, соответствующие количеству устройств в узлах. 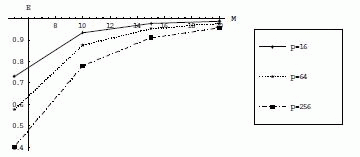

Эффективность параллельного алгоритма расчета модели Маркова на решетке процессоров в зависимости от количества решаемых задач М, устройств и процессоров не изменяется и равно 0.99 при М>20 (5). 
Реализация параллельного алгоритмаВычисление элемента матрицы переходных вероятностей не зависит от соседних элементов, следовательно, в основе параллельной реализации этой части параллельного алгоритма можно использовать принцип распараллеливания по данным. В качестве базовой подзадачи взят расчет строки матрицы переходных вероятностей, которая характеризуется одинаковой вычислительной трудоемкостью, что позволяет сбалансировать загрузку вычислительных модулей кластера. Каждый процесс определяет какие строки матрицы переходных вероятностей должет вичислить и отправить управляющему процессу. Схема параллельного алгоритма приведена на рис.7. 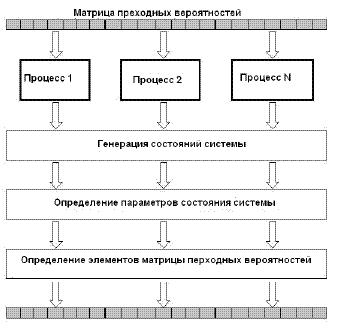
Расчет стационарных вероятностей реализован с использованием итерационного алгоритма, в котором в качестве базового используется алгоритм умноження матрицы на вектор. Схема алгоритма расчета вектора стационарных вероятностей представлена на рис.8. 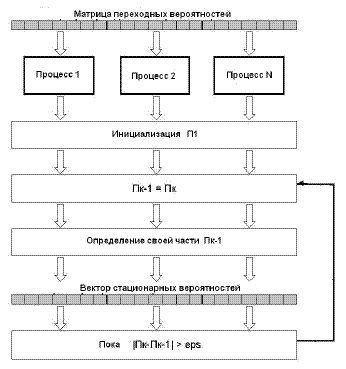
Расчет задачи проводилися на кластере, состоящего из двух, трех и четырех вычислительных модулей, реализованых на базе 19 процессоров AMD Athlon 3000+ (2Ггц), и сети Fast Ethernet. Общее время (в секундах) для расчета характеристик моделируемого кластера приведено в табл.1. Доля расчета матрицы переходных вероятностей от общего времени работы задачи составляет 0.65 (табл.2), что подтверждает теоретические расчеты. 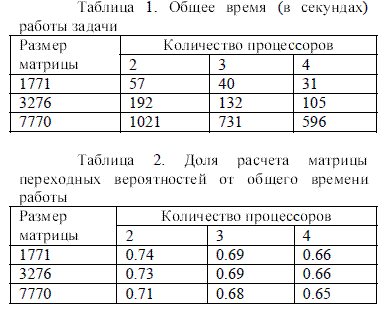
Ускорение параллельного алгоритма несколько (рис.9) хуже, чем теоретическое. Это объясняется тем, что топология кластера – «звезда», следовательно, время передачи между ВМ возрастает. Но несмотря на это, ускорение увеличивается с ростом количества процессоров для решаемых задач с количеством состояний 1771 и 3276. Для задачи с количеством состояний 56 ускорение меньше 0.5. Следовательно, для этой задачи количестсво обменов превышает количество вычислительных операций на ВМ. 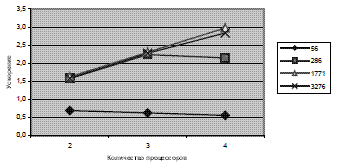
ВыводыПолученные оценки трудоемкости алгоритма дискретной Марковской модели кластера с совместным использованием дискового пространства, которые зависят от структуры вычислительной среды, от количества обрабатываемых задач и от особенностей матрицы переходных вероятностей, и оценки распараллеливания этого алгоритма на SIMD-структуры позволяют эффективно использовать параллельный алгоритм дискретной модели на высокопроизводительных ВС, который обеспечивает высокую точность расчетов. При реализации на кластере параллельного алгоритма дискретной марковской модели кластера доказана его достаточно высокая эффективность и ускорение при большой размерности решаемых задач. В дальнейшем можно определить оптимальное количество процессоров для распараллеливания подобных алгоритмов по критерию цена/производительность. Литература
|
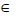 {1,0,-1} вычисляется
следующим образом
{1,0,-1} вычисляется
следующим образом
 – начальное распределение вероятностей состояний. Пусть Z=К – степень, при которой матрица Р не изменяется.
– начальное распределение вероятностей состояний. Пусть Z=К – степень, при которой матрица Р не изменяется.