The Neocognitron (Chapter 10)
Freeman J., Skapura D
Источник: Студенческий сайт ТНУ. Учебный раздел. Материалы для скачивания.
http://www.tnu.in.ua/study/downloads.php?do=file&id=4050
Functional Description
The neocognitron design evolved from an earlier model called the cognitron, and there are several versions of the neocognitron itself. The one that we shall describe has nine layers of PEs, including the retina layer. The system was designed to recognize the numerals 0 through 9, regardless of where they are placed in the field of view of the retina. Moreover, the network has a high degree of tolerance to distortion of the character and is fairly insensitive to the size of the character. This first architecture contains only feedforward connections.
The PEs of the neocognitron are organized into modules that we shall refer to as levels. Each level consists of two layers: a layer of simple cells, or S-cells, followed by a layer of complex cells, or C-cells. Each layer, in turn, is divided into a number of planes, each of which consists of a rectangular array of PEs. On a given level, the S-layer and the C-layer may or may not have the same number of planes. All planes on a given layer will have the same number of PEs; however, the number of PEs on the S-planes can be different from the number of PEs on the C-planes at the same level. Moreover, the number of PEs per plane can vary from level to level. There are also PEs called vs-cells and vr-cells that are not shown in the figure. These elements play an important role in the processing, but we can describe the functionality of the system without reference to them. We construct a complete network by combining an input layer, which we shall call the retina, with a number of levels in a hierarchical fashion. We call attention to the fact that there is nothing, in principle, that dictates a limit to the size of the network in terms of the number of levels.
The interconnection strategy is unlike that of networks that are fully interconnected between layers, such as the backpropagation network described in Chapter 3. Figure 10.5 shows a schematic illustration of the way units are connected in the neocognitron. Each layer of simple cells acts as a feature-extraction system that uses the layer preceding it as its input layer. On the first S-layer, the cells on each plane are sensitive to simple features on the retina - in this case, line segments at different orientation angles. Each S- cell on a single plane is sensitive to the same feature, but at different locations on the input layer. S-cells on different planes respond to different features.
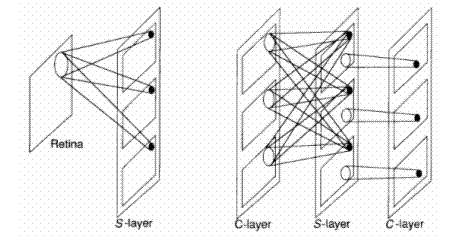
Figure 10.5 – A schematic representation of the interconnection strategy of the neocognitron
Note the slight difference between the first S -layer and subsequent S -layers in Figure 10.5. Each cell in a plane on the first S-layer receives inputs from a single input layer--namely, the retina. On subsequent layers, each S-cell plane receives inputs from each of the C-cell planes immediately preceding it. The situation is slightly different for the C-cell planes. Typically, each cell on a C-cell plane examines a small region of S-cells on a single S-cell plane. For example, the first C-cell plane on layer 2 would have connections to only a region of S-cells on the first S-cell plane of the previous layer. Reference back reveals that there is not necessarily a one-to-one correspondence between c-cell planes and S-cell planes at each layer in the system. This discrepancy occurs because the system designers found it advantageous to combine the inputs from some S-planes to a single C-plane if the features that the S-planes were detecting were similar. This tuning process is evident in several areas of the network architecture and processing equations.
The weights on connections to S-cells are determined by a training process that we shall describe in Section 10.2.2. Unlike in many other network architectures (such as backpropagation), where each unit has a different weight vector, all S-cells on a single plane share the same weight vector. Sharing weights in this manner means that all S-cells on a given plane respond to the identical feature in their receptive fields, as we indicated. Moreover, we need to train only one S-cell on each plane, then to distribute the resulting weights to the other cells.
The weights on connections to C-cells are not modifiable in the sense that they are not determined by a training process. All C-cell weights are usually determined by being tailored to the specific network architecture. As with S- planes, all cells on a single C-plane share the same weights. Moreover, in some implementations, all C-planes on a given layer share the same weights.
S-Cell Processing
We shall first concentrate on the cells in a single plane of Us1, as indicated in Figure 10.6. We shall assume that the retina, layer Uo, is an array of 19 by 19 pixels. Therefore, each Usl plane will have an array of 19 by 19 cells. Each plane scans the entire retina for a particular feature. As indicated in the figure, each cell on a plane is looking for the identical feature but in a different location on the retina. Each S-cell receives input connections h'om an array of 3 by 3 pixels on the retina. The receptive field of each S-cell corresponds to the 3 by 3 array centered on the pixel that corresponds to the cell's location on the plane.
When building or simulating this network, we must make allowances for edge effects. If we surround the active retina with inactive pixels (outputs always set to zero), then we can automatically account for cells whose fields of view are centered on edge pixels. Neighboring S-cells scan the retina array displaced by one pixel from each other. In this manner, the entire image is scanned from left to right and top to bottom by the cells in each S- plane.
A single plane of Vc-cells is associated with the S-layer, as indicated in Figure 10.6. The Vc-plane contains the same number of cells as does each S- plane. Vc-cells have the same receptive fields as the S-cells in corresponding locations in the plane. The output of a Vc-cell goes to a single S-cell in every plane in the layer. The S-cells that receive inputs from a particular Vc-cell are those that occupy a position in the plane corresponding to the position of the Vc-cell. The output of the Vc-cell has an inhibitory effect on the S-cells.
Up to now, we have been discussing the first S-layer, in which cells receive input connections from a single plane (in this case the retina) in the previous layer. For what follows, we shall generalize our discussion to include the case of layers deeper in the network where an S-cell will receive input connections from all the planes on the previous C-layer.
Figure 10.6 – S-cell structure
Let the index k1 refer to the kth plane on level 1. We can label each cell on a plane with a two-dimensional vector, with n indicating its position on the plane; then, we let the vector v refer to the relative position of a cell in the previous layer lying in the receptive field of unit n. With these definitions, we can write the following equation for the output of any S-cell:
(10.1)
Function given by :
(10.2)
We must now specify the output from the inhibitory nodes. The Vc-cell at position n has an output value of :
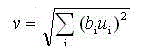(10.3)
where bi is the weight on the connection fi'om a cell m position v of the Vc-cell's receptive field. These weights are not subject to training. They can take the fore of any normalized hnction that decreases monotonically as the magnitude of v increases.
The particular form of Eq. (10.3) is that of a weighted, mot-mean-square of the inputs to the Vc-cell. Looking back at Eq. (10.1), we can see that, in the S-cells, the net excitatory input to the cell is being compared to a measure of the average input signal. If the ratio of the net excitatory input to the net inhibitory input is greater than 1, the cell will have a positive output.
Training Weights on the S-Layers
There are several different methods for training the weights on the neocognitron. The method that we shall detail here is an unsupervised-leaming algorithm designed by the original neocognitron designers.
In principle, training proceeds as it does for many networks. First, an input pattern is presented at the input layer and the data are propagated tln'ough the network. Then, weights are allowed to make incremental adjustments according to the specified algorithm. After weight updates have occurred, a new pattern is presented at the input layer, and the process is repeated with all patterns in the training set until the network is classifying the input patterns properly.
In the neocognitron, sharing of weights on a given plane means that only a single cell on each plane needs to participate in the learning process. Once its weights have been updated, a copy of the new weight vector can be distributed to the other cells on the same plane. To understand how this works, we can think of the S-planes on a given layer as being stacked vertically on top of one another, aligned so that cells at corresponding locations are directly on top of one another. We can now imagine many overlapping columns running perpendicular to this stack. These columns define groups of S-cells, where all of the members in a group have receptive fields in approximately the same location of the input layer.
Processing on the C-cell
The functions describing the C-cell processing are similar in form to those for the S-cells. Also like the S-layer, each C-layer has associated with it a single plane of inhibitory units that function in a manner similar to the re-cells on the S-layer. We label the output of these units Vs.
Generally, units on a given C-plane receive input connections from one, or at most a small number of, S-planes on the preceding layer. Vs-cells receive input connections from all S-planes on the preceding layer.
The output of a C-cell is given by:
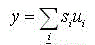(10.4)
where si – output signal from the simple neurons;
ui – weight coefficientsfrom simple neurons to complex.
For neurons from the complex layer we can use different activation functions.
In summary, only a certain percentage of S-ceils and C-cells at each level respond with a positive output value. These are the cells whose excitation level exceeds that of the average cells.