Е. Теллєр
Актуальність теми
Цифрові системи знаходять широке застосування та виступають базовими компонентами комп'ютерної техніки, автоматики, робототехніки, виробництва, транспорту. Створення надвеликих інтегральних схем (НВІС), побудова систем-на-кристалі (SoC – System-on-Chip), розвиток технологій програмованих користувачем вентильних матриць (FPGAs – Field-Programmable Gate Arrays) та складних програмованих логічних пристроїв (CPLDs – Complex Programmable Logic Devices) змінили базис реалізації цифрових систем і висунули підвищені вимоги до процесу їх розробки, що привело до широкого розповсюдження систем автоматизованого проектування (САПР) і мов опису апаратури (HDLs – Hardware Description Languages), які повинні сприяти підвищенню якості результуючого продукту, інтенсифікації проектних робіт, всебічному аналізу та тестуванню. Крім того, були створені нові, базисно-орієнтовані методи синтезу комбінаційних і послідовністних логічних схем, найбільша ефективніть від застосування яких може бути досягнута шляхом автоматизації і сумісного комбінованого використання з вже відомими алгоритмами.
Модель кінцевого автомата, запропонована Е. Муром у 1956 році та названа на його честь (автомат Мура), як синхронна послідовністна схема, є частиною багатьох цифрових систем і застосовується при побудові пристроїв керування. Висока складність інтегральних схем (яка продовжує підвищуватися, за законом Г. Мура) і теоретичний базис автоматних обчислень робить можливою реалізацію комплексних алгоритмів обробки інформації. Проте, безпосередня реалізація алгоритмів може приводити до неефективного використання ресурсів кристалу та підвищення вартості проекту.
Відомий ряд методів апаратурної оптимізації автомата Мура: мінімізація кількості станів та їх специфічне кодування, використання особливостей цільового базису та алгоритма функціонування, багаторівнева реалізація логічної схеми. Вказані методи володіють визначеною ефективністю, але, для отримання найбільш економічної реалізації автомата, повинні використовуватися сумісно.
Магістерська робота присвячена актуальній науковій задачі розробки уніфікованого підходу до синтезу автоматів Мура, спрямованого на зменшення апаратурних витрат у результуючому пристрої та складеного з алгоритмічних, комбінаторних та схемотехнічних оптимізаційних прийомів. У якості цільового базису використовуються мікросхеми FPGA фірми Xilinx, що сполучають функціональність, програмованість, реконфігурованість і доступність широкому споживачу, а інструментальними засобами дослідження виступають САПР Xilinx ISE, Verilog HDL і Java SE.
Мета та задачі дослідження
Метою дослідження є розробка підходу до уніфікації синтезу автоматів Мура, спрямованого на зменшення апаратурних витрат у цільовій FPGA-мікросхемі.
Основні задачі дослідження:
- Аналіз методів мінімізації кількості станів у повністю визначених та часткових автоматах Мура.
- Оцінка способів зменшення апаратурних витрат шляхом кодування станів автоматів Мура.
- Пошук і виявлення характеристик існуючих методів побудови логічних схем автоматів Мура та оцінка можливостей їх застосування в базисі FPGA.
- Об'єднання функціонально різних напрямів оптимізації автоматів Мура за апаратурними витратами в уніфікований підхід до синтезу та формування рекомендацій по його використанню.
- Розробка альтернативних варіантів основних етапів уніфікованого процесу синтезу автоматів Мура та оцінка їх ефективності.
Об'єкт дослідження: синтез автоматів Мура.
Предмет дослідження: об'єднання методів зменшення апаратурних витрат при реалізації автоматів Мура в базисі мікросхем FPGA.
Передбачувана наукова новизна
В рамках магістерської роботи планується отримання актуальних наукових результатів по наступним напрямкам:
- Розробка підходу до уніфікації синтезу автоматів Мура, орієнтованого на зменшення апаратурних витрат та побудованого на базі останніх досягнень абстрактної і структурної теорії автоматів.
- Визначення областей застосування різних варіантів основних етапів уніфікованого процесу синтезу автоматів Мура.
- Модифікація відомих методів побудови логічних схем автоматів Мура та оцінка ефективності їх застосування в базисі FPGA.
Заплановані практичні результати
Для експериментальної оцінки отриманих теоретичних результатів і формування фундаменту наступних досліджень, планується розробка кросплатформової, налаштовуваної і функціональної системи автоматизованого проектування автоматів Мура (САПРАМ) з наступними властивостями:
- Наявність власної XML-орієнтованої мови опису автоматів Мура.
- Реалізація підходу до уніфікації синтезу автоматів Мура, спрямованого на базис FPGA-мікросхем фірми Xilinx.
- Можливість управління складом уніфікованого процесу синтезу автоматів Мура та варіантами основних його етапів.
- Генерування Verilog-файлу, що описує синтезований автомат Мура та придатний для обробки САПР Xilinx ISE з метою завантаження до мікросхеми FPGA.
Огляд досліджень і розробок
Оскільки автомати Мура є важливою частиною цифрових систем, то проблеми їх синтезу, аналізу, мінімізації і реалізації були широко досліджені як американськими, європейськими, японськими вченими, так і вітчизняними спеціалістами. Питанням реалізації цифрових пристроїв за допомогою FPGA і Verilog HDL також присвячений ряд робіт, головним чином, дослідників західної школи.
Глобальний огляд
Концепція автомата Мура була сформульована Е. Муром у його статті «Gedanken-experiments on sequential machines» [1]. Там же показана сфера застосування моделей з кінцевою кількістю станів і розглядається широкий клас проблем абстрактної теорії автоматів. Іншими джерелами інформації про класифікації, фундаментальні принципи функціонування, способи представлення, математичний зміст і застосування кінцевих автоматів можуть служити монографії Р. Міллера, А. Гілла, Д. Хопкрофта, М. Мінського, М. Іто [2-6].
При розробці цифрових систем, автомати Мура реалізуються як синхронні послідовністні схеми, процеси аналізу та синтезу яких докладно викладені в сучасних книгах по логічному проектуванню В. Нельсона, К. Брідінга, Д. Уейкерлі, М. Мано, Б. Уілкінсона та ін. [7-16]. Питанням використання мови опису апаратури Verilog при проектуванні, моделюванні та реалізації цифрових пристроїв присвячені роботи П. Чу, М. Чілетті, П. Ашендена, С. Палніткара, А.К. Полякова [17-25]. Мікросхеми FPGA – їх архітектури, властивості, області застосування – є предметом розгляду у К. Максфілда, І. Гроута, Б. Зайдмана, Р.І. Грушвицького, О.Х. Мурсаєва, Є.П. Угрюмова [26-29].
В класичних роботах В.М. Глушкова та С.І. Баранова [30, 31] викладена абстрактна та структурна теорія автоматів, сформульований канонічний метод структурного синтезу цифрового автомата, розроблені питання матричної реалізації логічних схем.
Мінімізація кількості станів автоматів Мура – важливий крок проектування, оскільки саме кількість станів визначає розрядність кодувального двійкового слова при структурному синтезі. Підходи до рішення цієї задачі в різний час розроблювалися та довершувалися М. Аведілло, Х. Куінтаною та Х. Хуертасом (алгоритм ARNES, алгоритм SMAS) [32, 33]; Х.-М. Чампарнаудом, А. Хорсі та Т. Парантоеном (модифікация алгоритма Бржожовські) [34]; С. Гореном та Ф. Фергюсоном (алгоритм CHESMIN) [35]; Х. Хігучі та Ю. Мацунагою (алгоритм SLIM) [36]; Х. Ху, Х.-К. Ксуе та Д.-Н. Біаном (алгоритм HSM2) [37]; Д.-К. Рхо, Г. Хачтелем, Ф. Соменці та Р. Якобі (алгоритм STAMINA) [38]; Д. Хопкрофтом (найбільш ефективний існуючий алгоритм мінімізації) [39]; Р. Фурером та С. Новіком (алгоритм OPTIMIST) [40]; Х. Пеною та А. Олівейрою (алгоритм BICA) [41]; Т. Камом, Т. Віллою, Р. Брайтоном та А. Санджиованні-Винцентеллі (алгоритм ISM) [42]. Деякі методи мінімізації повністю визначених і часткових автоматів оцінені та описані в роботах [14, 43].
Критичним для рівня апаратурних витрат логічної схеми автомата Мура виступає етап кодування станів, короткий опис підходів до якого міститься в оглядовій статті А. Слюсарчука [44]. В публікаціях Д. Де Мішелі, Р. Брайтона, А. Санджиованні-Винцентеллі, А. Ель-Малеха, С. Саіта, Ф. Кхана наведені ефективні алгоритми кодування станів кінцевих автоматів і пристроїв керування на їх основі [45-48]. Оригінальні способи оптимізації кодування та багаторівневої реалізації розглянуті в роботах С. Девадаса, Х.-К. Ма, А. Ньютона та А. Санджиованні-Винцентеллі (алгоритм MUSTANG) [49]; К. Ду, Г. Хачтеля, Б. Ліна та А. Ньютона (алгоритм MUSE) [50]; Х. Кубатової та М. Беквара (алгоритм FEL-Code) [51]; Б. Ліна та А. Ньютона (алгоритм JEDI) [52]; Т. Вілли та А. Санджиованні-Винцентеллі (алгоритм NOVA) [53]; Б. Гупти, Х. Нараянана та М. Десая (алгоритм Two-Hot Encoding) [54]; М. Мартінеса, М. Аведілло, Х. Куінтани та Х. Хуертаса (алгоритм DISA) [55]. Відомий унітарний спосіб кодування станів і його застосування до проектування автоматів для FPGA описані у С. Голсона [56].
Використання апарату еволюційних і генетичних обчислень до кодування станів автоматів розглянуто в [57-61]. Перші паралельні алгоритми кодування станів, призначені для виконання на високопродуктивній комп'ютерній техніці, – ProperSTATE і ProperJEDI – були запропоновані в 1996 році Г. Хастеєром у рамках проекту ProperCAD [62]. У 2004 році Д. Бадер і К. Маддурі представили паралельний алгоритм кодування станів, орієнтований на симетричні мультипроцесорні системи (SMP-системи), що відносяться до класу MIMD [63].
Апаратурно-оптимальна реалізація логічної схеми автомата Мура залежить від використовуваного цільового базису. В роботах О.О. Баркалова, Л.О. Титаренко, С. Хмелевського, А. Буковця, Г. Селварая, М. Равські, Т. Луби, В.А. Склярова, Р. Червінські, Д. Каніа розглядаються методи побудови кінцевих автоматів на базі CPLD, FPGA і вбудованих блоків пам'яті ROM (Read-Only Memory) [64-68]. У статті О.О. Баркалова, Л.О. Титаренко та О. Хебди пропонується спосіб нестандартного представлення кодів станів, орієнтований на базис CPLD і дозволяючий оптимізувати логічну схему автомата Мура [69].
Комплексний огляд процесу синтезу автоматів Мура та Мілі (з акцентом на можливості його автоматизації), а також численна тематична бібліографія міститься в статті М. Перковські [70]. Прикладом реалізованої програмної системи синтезу та оптимізації послідовністних схем є SIS, розроблена в Каліфорнійському університеті (США) та докладно висвітлена в роботі [71].
Національний огляд
У Одеському національному політехнічному університеті Є.Л. Поліним, К.В. Защолкіним, Ю.А. Ковальовим, О.М. Івановою, А.А. Ніколенко активно розроблюються паралельні моделі мови граф-схем алгоритмів (ГСА), методи синтезу цифрових керуючих пристроїв, абстрактні композиційні автомати, питання інформаційної технології автоматизованого проектування мікропрограмних автоматів [72-76].
І.В. Васильцовим (Тернопільська академія національної економіки) запропонований еволюційний підхід до кодування внутрішніх станів кінцевого автомата [77], а в статтях Л.А. Шувалової, Д.Н. Моамара, Т.Ю. Уткіної (Черкаський державний технологічний університет) [78] і С.М. Сердюка (Запорізький національний технічний університет) [79] розглянуті можливості автоматизованого аналізу, синтезу та верифікації цифрових автоматів.
Проектування цифрових пристроїв у базисі FPGA докладно висвітлено в роботах В.І. Жабіна, М.А. Ковальова (НТУУ «Київський політехнічний університет») [80] та В.М. Опанасенка, О.М. Лісового, Є.В. Сороки (Інститут кібернетики ім. В.М. Глушкова НАН України) [81, 82].
Локальний огляд
У Донецькому національному технічному університеті (кафедра комп'ютерної інженерії) широко розроблюються методи реалізації логічних схем кінцевих автоматів, мікропрограмних пристроїв керування (МПК) та композиційних мікропрограмних пристроїв керування (КМПК) в базисах SPLD (Simple Programmable Logic Device), CPLD, FPGA, ASIC (Application Specific Integrated Circuit).
У книгах О.О. Баркалова та Л.О. Титаренко детально розглянуті алгоритми побудови керуючих (КА) і операційних (ОА) автоматів, об'єднуваних для реалізації цифрових пристроїв [83-85]. У якості одного з способів організації КА часто використовуються автомати Мура та Мілі [30], дослідження апаратурної оптимізації яких дозволило авторам розробити ряд оригінальних підходів до синтезу логічних схем КА з «жорсткою логікою»: багаторівневі структури, принцип перетворення кодів об'єктів, можливості модифікації вихідних граф-схем алгоритмів (ГСА), реалізації на лічильниках, використання блоків пам'яті.
Статті О.О. Баркалова, С.О. Ковальова, С.О. Цололо, А.В. Матвієнка, В.О. Саломатіна, О.О. Красічкова присвячені оптимізації логічної схеми автомата Мура, реалізуємої на CPLD, однорідних програмованих логічних інтегральних схемах (ПЛІС), FPGA [86-90]. Автори пропонують використовувати поняття псевдоеквівалентності станів, особливості цільового базису, специфічні способи кодування внутрішніх станів. Для ефективної реалізації автоматів Мура на замовлених схемах (ASICs), О.О. Баркаловым, Р.В. Мальчевою та К.А. Солдатовим були запропоновані метод кодування наборів мікрооперацій і принцип розширення кодів станів переходу [91, 92].
Тематика адаптації UML (Unified Modeling Language), MDA (Model-Driven Architecture) і високопродуктивних комп'ютерних технологій (паралельних та розподілених систем) до синтезу та моделювання КА широко висвітлена в публікаціях О.О. Баркалова, І.Я. Зеленьової, А.О. Гриценка, С.О. Ковальова [93-96].
Підхід до уніфікації синтезу автоматів Мура в базисі FPGA
Перші мікросхеми FPGA були розроблені фірмою Xilinx у 1984 році та набули великої популярності, завдяки можливості реалізації складних функцій і відносно невеликій вартості. Сучасні FPGA поєднують програмованість SPLD і CPLD, зберігаючи основну перевагу ASIC – об'єм реалізуємих функцій [27].
Неоптимізовані проекти цифрових систем, незалежно від базису реалізації, можуть мати значну надлишковість і, отже, неефективно використовувати апаратні ресурси [84]. Це приводить до актуалізації задачі апаратурної оптимізації, яка, в контексті FPGA, зводиться до зниження відсотка використання тих чи інших внутрішніх блоків: LUT-елементів (LUT – Look-Up Table), модулів пам'яті, схем синхронізації.
Апаратурно-оптимальна реалізація автоматів Мура потребує сумісного застосування результатів абстрактної і структурної теорії автоматів: мінімізації кількості станів (зменшення потужності множини станів автомата та, як наслідок, розрядності двійкового коду стану), ефективного кодування станів (зниження рівня витрат при реалізації функцій наступного стану), адаптації логічної схеми до використовуваного базису (якісне розподілення ресурсів кристалу за рахунок використання вбудованих блоків пам'яті та особливостей організації внутрішніх модулів).
У статті [97] пропонується підхід до уніфікації синтезу автоматів Мура, що поєднує вказані можливості оптимізації і направлений на базис мікросхем FPGA (рис. 1). Сутність цього підходу полягає у послідовному застосуванні алгоритмічного, комбінаторного та схемотехнічного етапів і використанні FPGA-орієнтованих інструментальних засобів: САПР і HDLs.
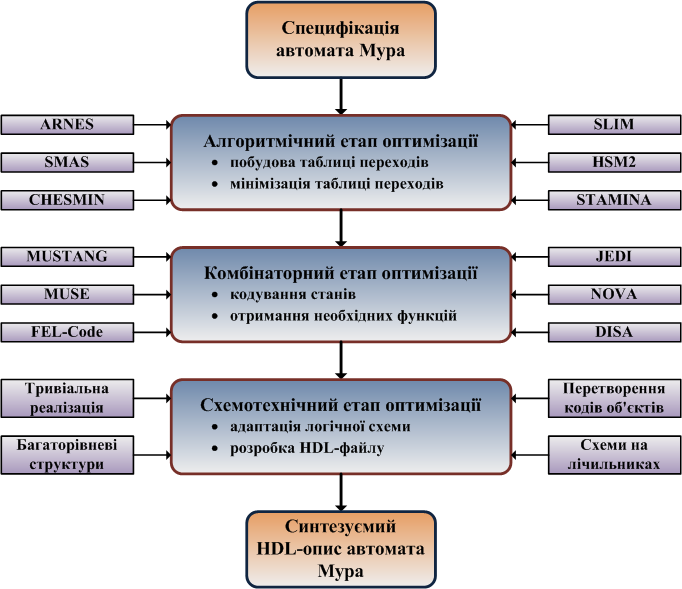
Рисунок 1 – Підхід до уніфікації синтезу автоматів Мура
На першому кроці алгоритмічного етапу синтезу, деяка специфікація автомата Мура приводиться до єдиного вигляду – таблиці переходів. Необхідність приведення пов'язана з тим, що автомат Мура може бути заданий із використанням різних форм представлення: граф-схем, діаграм станів, ASM-діаграм (ASM – Algorithmic State Machine) [13, 14, 83]. Другий крок алгоритмічного етапу полягає в мінімізації кількості станів таблиці переходів. Для цього можуть використовуватися алгоритми Бржожовські, ARNES, SMAS, CHESMIN, SLIM, HSM2, STAMINA, OPTIMIST, BICA, ISM [14, 32-43].
Комбінаторний етап направлений на ефективне кодування станів мінімізованої таблиці переходів, а також отримання апаратурно-мінімальних функцій наступного стану та, при необхідності, результуючих функций автомата. Значний вплив способу кодування станів на параметри результуючої логічної схеми зумовило розробку різних підходів, направлених на зниження витрат потужності, підвищення швидкодії, мінімізацію апаратурних витрат. Останній з цих підходів може бути використаний на комбінаторному етапі синтезу шляхом застосування, адаптації або модифікації алгоритмів MUSTANG, MUSE, FEL-Code, JEDI, NOVA, Two-Hot Encoding, DISA, унітарного та позиційно-двійкового кодування станів [44-63, 84].
Схемотехнічний етап процесу синтезу передбачає використання методів побудови логічної схеми автомата Мура, направлених на зменшення апаратурних витрат цільової мікросхеми. До таких методів відносяться тривіальні та багаторівневі реалізації, структури з перетворенням кодів об'єктів, схеми на лічильниках [84]. Оскільки сучасне цифрове проектування на мікросхемах FPGA орієнтоване на використання HDLs (в основному, VHDL і Verilog), то другим кроком схемотехнічного етапу виступає розробка HDL-програми, що описує автомат Мура та придатна для обробки відповідною САПР і завантаження до мікросхеми.
Описаний уніфікований процес синтезу може бути з успіхом реалізований автоматизовано та передбачати тільки управлінські функції користувача: опис автомата Мура та вибір використовуваних алгоритмів і структур. Крім того, представлений підхід може застосовуватися до ряду інших сучасних базисів (CPLD, ASIC) і визначати загальний напрямок оптимізаційних робіт при синтезі логічних послідовністних схем.
Для оцінки ефективності застосування уніфікованого процесу синтезу до конкретного прикладу, були розроблені п'ять Verilog-програм, що описують заданий автомат Мура [8] (рис. 2) різними способами:

Рисунок 2 – Діаграма станів автомата Мура
(анімація: 10 кадрів, 5 циклів повторення, 160 кілобайт)
(xi – вихідні сигнали, yi – біти коду стану, zi – результуючі сигнали)
- Реалізація немінімізованого автомата Мура за допомогою аналізатора XST (Xilinx Synthesis Technology) [98] (експеримент 1).
- Реалізація мінімізованого автомата Мура за допомогою аналізатора XST (експеримент 2).
- Реалізація мінімізованого автомата Мура за двохрівневою схемою [85] з позиційно-двійковим кодуванням станів. Використання ROM з асинхронним читанням [98] (експеримент 3).
- Реалізація мінімізованого автомата Мура за двохрівневою схемою з позиційно-двійковим кодуванням станів. Використання ROM з синхронним читанням [98] і додаткового сигналу синхронізації (експеримент 4).
- Реалізація мінімізованого автомата Мура за двохрівневою схемою з позиційно-двійковим кодуванням станів. Використання ROM з синхронним читанням і заднього фронту основного сигналу синхронізації (експеримент 5).
Усі дослідження проводилися за допомогою САПР Xilinx ISE 13.1 для сімейства FPGA Xilinx Spartan-3, а саме для мікросхеми XC3S200. Результати сукупних апаратурних витрат для п'яти варіантів реалізації графічно показані на рис. 3.
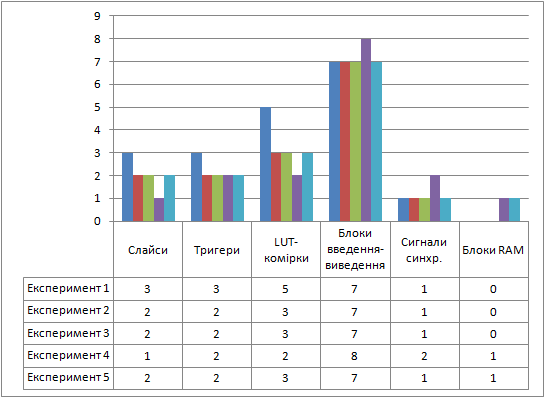
Рисунок 3 – Результати експериментальних досліджень
Якщо метою оптимізації була кількість LUT-комірок, то кращий результат був отриманий при використанні двохрівневої реалізації мінімізованого автомата Мура з синхронним ROM і двома сигналами синхронізації (експеримент 4). У порівнянні з експериментом 1, кількість слайсів зменшилася в 3 рази, кількість тригерів – в 1,5 рази, а кількість LUT-комірок – в 2,5 рази. Проте, в цьому випадку збільшилася загальна кількість виводів схеми, кількість сигналів синхронізації і був задіяний один модуль RAM (Random Access Memory).
Завершення
Якісний синтез цифрових систем, і автоматів Мура зокрема, є одним з напрямів логічного проектування й представляє не тільки теоретико-дослідницький, але й практичний інтерес. Розробка оптимальних цифрових пристроїв відкриває шлях до більш повного використання можливостей базису реалізації, «зщільнення» проектів, зменшення матеріальних витрат.
Магістерська робота присвячена актуальній науковій задачі об'єднання основних методів апаратурної мінімізації автоматів Мура. В рамках проведених досліджень виконано:
- Розроблена структура уніфікованого процесу синтезу автоматів Мура та визначені функції її складових.
- На підставі аналізу літературних джерел виділені основні алгоритми, що можуть бути використані в запропонованому підході до уніфікації синтезу автоматів Мура.
- Проведений ряд експериментів по використанню уніфікованого процесу синтезу автоматів Мура, проаналізовані отримані результати.
- Розглянуті можливості комплексної автоматизації розробленого підходу до уніфікації синтезу автоматів Мура, оцінені вимоги до програмного забезпечення, виконаний пошук функціонально подібних програмних продуктів синтезу послідовністних логічних схем.
Подальші дослідження направлені на наступні аспекти:
- Якісне вдосконалення запропонованого підходу до уніфікації синтезу автоматів Мура, його доповнення та розширення.
- Визначення границь ефективності різних варіантів основних етапів уніфікованого процесу синтезу автоматів Мура.
- Адаптація відомих методів побудови логічних схем автоматів Мура до базису FPGA.
- Розробка кросплатформової і функціональної системи автоматизованого проектування автоматів Мура (САПРАМ), що реалізує запропонований уніфікований процес синтезу.
При написанні даного реферату магістерська робота ще не завершена. Остаточне завершення: грудень 2011 року. Повний текст роботи та матеріали по темі можуть бути отримані у автора або його керівника після вказаної дати.
Перелік посилань
- Moore E.F. Gedanken-experiments on sequential machines / E.F. Moore // Automata studies, Annals of mathematical studies. – 1956. – vol. 34. – pp. 129-153.
- Гилл А. Введение в теорию конечных автоматов / А. Гилл. – М.: Наука, 1966. – 272 с.
- Миллер Р. Теория переключательных схем / Р. Миллер. – М.: Наука, 1971. – Том 2: Последовательностные схемы и машины. – 304 с.
- Минский М. Вычисления и автоматы / М. Минский. – М.: Мир, 1971. – 364 с.
- Хопкрофт Д. Введение в теорию автоматов, языков и вычислений / Д. Хопкрофт, Р. Мотвани, Д. Ульман. – М.: Издательский дом «Вильямс», 2002. – 528 с.
- Ito M. Algebraic theory of automata and languages / M. Ito. – World Scientific Publishing, 2004. – 199 pp.
- Голдсуорт Б. Проектирование цифровых логических устройств / Б. Голдсуорт. – М.: Машиностроение, 1985. – 288 с.
- Уилкинсон Б. Основы проектирования цифровых схем / Б. Уилкинсон. – М.: Издательский дом «Вильямс», 2004. – 320 с.
- Уэйкерли Д. Проектирование цифровых устройств / Д. Уэйкерли. – М.: Постмаркет, 2002. – Том 2. – 528 с.
- Breeding K. Digital design fundamentals / K. Breeding. – Prentice Hall, 1992. – 446 pp.
- Holdsworth B. Digital logic design / B. Holdsworth, C. Woods. – Prentice Hall, 2002. – 519 pp.
- Lala P. Principles of modern digital design / P. Lala. – Wiley, 2007. – 419 pp.
- Mano M. Digital design / M. Mano. – Prentice Hall, 2003. – 516 pp.
- Nelson V. Digital logic circuit analysis and design / V. Nelson, H. Nagle, J. Irwin, B. Carroll. – Prentice Hall, 1995. – 842 pp.
- Shiva S. Introduction to logic design / S. Shiva. – CRC Press, 1998. – 628 pp.
- Singh A. Foundation of switching theory and logic design / A. Singh. – New Age International, 2008. – 412 pp.
- Поляков А.К. Языки VHDL и VERILOG в проектировании цифровой аппаратуры / А.К. Поляков. – М.: СОЛОН-Пресс, 2003. – 320 с.
- Ashenden P. Digital design: an embedded systems approach using Verilog / P. Ashenden. – Morgan Kaufmann Publishers, 2008. – 557 pp.
- Chu P. FPGA prototyping by Verilog examples / P. Chu. – Wiley, 2008. – 488 pp.
- Ciletti M. Advanced digital design with the Verilog HDL / M. Ciletti. – Prentice Hall, 2005. – 986 pp.
- Minns P. FSM-based digital design using Verilog HDL / P. Minns, I. Elliott. – Wiley, 2008. – 391 pp.
- Lee J. Verilog quickstart: a practical guide to simulation and synthesis in Verilog / J. Lee. – Springer, 2002. – 355 pp.
- Lee W. Verilog coding for logic synthesis / W. Lee. – Wiley, 2003. – 336 pp.
- Padmanabhan T. Design through Verilog HDL / T. Padmanabhan, B. Bala Tripura Sundari. – Wiley, 2004. – 455 pp.
- Palnitkar S. Verilog HDL. A guide to digital design and synthesis / S. Palnitkar. – SunSoft Press, 1996. – 396 pp.
- Грушвицкий Р.И. Проектирование систем на микросхемах программируемой логики / Р.И. Грушвицкий, А.Х. Мурсаев, Е.П. Угрюмов. – СПб.: БХВ-Петербург, 2002. – 608 с.
- Максфилд К. Проектирование на ПЛИС. Курс молодого бойца / К. Максфилд. – М.: Издательский дом «Додэка-XXI», 2007. – 408 с.
- Grout I. Digital systems design with FPGAs / I. Grout. – Elsevier, 2008. – 724 pp.
- Zeidman B. Designing with FPGAs and CPLDs / B. Zeidman. – Elsevier, 2002. – 224 pp.
- Баранов С.И. Синтез микропрограммных автоматов (граф-схемы и автоматы) / С.И. Баранов. – Л.: Энергия, 1979. – 232 с.
- Глушков В.М. Синтез цифровых автоматов / В.М. Глушков. – М.: Государственное издательство физико-математической литературы, 1962. – 476 с.
- Avedillo M.J. New approach to the state reduction in incompletely specified sequential machines / M.J. Avedillo, J.M. Quintana, J.L. Huertas // Proceedings of IEEE International Symposium on Circuits and Systems. – New Orleans, 1990. – pp. 440-443.
- Avedillo M.J. SMAS: a program for the concurrent state reduction and state assignment of finite state machines / M.J. Avedillo, J.M. Quintana, J.L. Huertas // Proceedings of IEEE International Symposium on Circuits and Systems. – 1991. – vol. 3. – pp. 1781-1784.
- Champarnaud J.-M. Split and minimizing: Brzozowski's algorithm / J.-M. Champarnaud, A. Khorsi, T. Paranthoen // Prague Stringology Conference. – Prague, 2002. – pp. 96-104.
- Goren S. CHESMIN: a heuristic for state reduction in incompletely specified finite state machines / S. Goren, F. Ferguson // Proceedings of the Conference on Design, Automation and Test in Europe. – 2002. – pp. 248-254.
- Higuchi H. A fast state reduction algorithm for incompletely specified finite state machines / H. Higuchi, Y. Matsunaga // 33rd Annual Conference of Design Automation. – Las Vegas, 1996. – pp. 463-466.
- Hu H. HSM2: a new heuristic state minimization algorithm for finite state machine / H. Hu, H.-X. Xue, J.-N. Bian // Journal of Computer Science and Technology. – 2004. – № 19 (5). – pp. 729-733.
- Rho J.-K. Exact and heuristic algorithms for the minimization of incompletely specified state machines / J.-K. Rho, G. Hachtel, F. Somenzi, R. Jacoby // IEEE Transactions on Computer-Aided Design. – 1994. – vol. 13. – pp. 167-177.
- Xu Y. Describing an n log n algorithm for minimizing states in deterministic finite automaton [Электронный ресурс]. – Режим доступа: http://www.cs.sun.ac.za/rw711/documentation/hopcroft2.pdf.
- Fuhrer R.M. OPTIMIST: state minimization for optimal 2-level logic implementation / R.M. Fuhrer, S.M. Nowick // Proceedings of International Conference of Computer-Aided Design. – 1997. – pp. 308-315.
- Pena J.M. A new algorithm for exact reduction of incompletely specified finite state machines / J.M. Pena, A.L. Oliveira // IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. – 1999. – vol. 18 (11). – pp. 1619-1632.
- Kam T. A fully implicit algorithm for exact state minimization / T. Kam, T. Villa, R. Brayton, A. Sangiovanni-Vincentelli // Proceedings of the Design Automation Conference. – 1994. – pp. 684-690.
- Almeida M. On the performance of automata minimization algorithms / M. Almeida, N. Moreira, R. Reis // Technical Report Series: DCC-2007-03. – 2007. – 12 pp.
- Slusarczyk A. State assignment techniques – short review [Электронный ресурс]. – Режим доступа: http://web.cecs.pdx.edu/~mperkows/nov17/051.slusarczyk-state-assignment-review.pdf.
- De Micheli G. KISS: a program for optimal state assignment of finite state machines / G. De Micheli, R. Brayton, A. Sangiovanni-Vincentelli // Proceedings of IEEE International Conference of Computer-Aided Design. – Santa Clara, 1984. – pp. 209-211.
- De Micheli G. Optimal state assignment for finite state machines / G. De Micheli, R. Brayton, A. Sangiovanni-Vincentelli // IEEE Transactions on Computer-Aided Design. – 1985. – pp. 269-285.
- De Micheli G. Optimal encoding of control logic / G. De Micheli // Proceedings of the International Conference on Circuits and Computer Design. – 1984. – pp. 16-22.
- El-Maleh A. Finite state machine state assignment for area and power minimization / A. El-Maleh, S.M. Sait, F.N. Khan // Proceedings of IEEE International Symposium on Circuits and Systems. – 2006. – pp. 5303-5306.
- Devadas S. MUSTANG: state assignment of finite state machines targeting multilevel logic implementations / S. Devadas, H.-K. Ma, A.R. Newton, A. Sangiovanni-Vincentelli // IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. – 1998. – vol. 7 (12). – pp. 1290-1300.
- Du X. MUSE: a multilevel symbolic encoding algorithm for state assignment / X. Du, G. Hachtel, B. Lin, A.R. Newton // IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. – 1991. – vol. 10 (1). – pp. 28-38.
- Kubatova H. FEL-Code: FSM internal state encoding method / H. Kubatova, M. Becvar // Proceedings of 5th International Workshop on Boolean Problems. – Freiberg, 2002. – pp. 109-114.
- Lin B. Synthesis of multiple level logic from symbolic high-level description languages / B. Lin, A.R. Newton // Proceedings of the International Conference on VLSI. – Munich, 1989. – pp. 187-196.
- Villa T. NOVA: state assignment of finite-state machines for optimal two-level logic implementation / T. Villa, A. Sangiovanni-Vincentelli // IEEE Transactions on Computer-Aided Design. – 1990. – pp. 905-924.
- Gupta, B.N.V.M. A state assignment scheme targeting performance and area / B.N.V.M. Gupta, H. Narayanan, M.P. Desai // Proceedings of 12th International Conference on VLSI Design. – 1999. – pp. 378-383.
- Martinez M. A dynamic model for the state assignment problem / M. Martinez, M.J. Avedillo, J.M. Quintana, J.L. Huertas // Proceedings of Design, Automation and Test in Europe. – Paris, 1998. – pp. 835-839.
- Golson S. One-hot state machine design for FPGAs / S. Golson // Proceedings of the 3rd PLD Design Conference. – Santa Clara, 1993. – pp. 1-6.
- Almaini A. State assignment of finite state machines using a genetic algorithm / A. Almaini, J. Miller, P. Thomson, S. Billina // IEEE Proceedings on Computer and Digital Techniques. – 1995. – pp. 279-286.
- Amaral J. Designing genetic algorithms for the state assignment problem / J. Amaral, K. Turner, J. Chosh // IEEE Transactions on Systems, Man, and Cybernetics. – 1995. – vol. 25. – pp. 659-694.
- Chyzy M. Evolutionary algorithm for state assignment of finite state machines / M. Chyzy, W. Kosinski // Artificial Intelligence Methods. – Gliwice, 2003. – pp. 51-52.
- Nedjah N. Evolutionary synthesis of synchronous finite state machines / N. Nedjah, L.M. Mourelle // Evolvable Machines. – Berlin, 2004. – pp. 103-128.
- Chattopadhyay S. Area conscious state assignment with flip-flop and output polarity selection for finite state machine synthesis – a genetic algorithm approach / S. Chattopadhyay // The Computer Journal. – 2005. – vol. 48 (4). – pp. 443-450.
- Hasteer G. Parallel algorithms for state assignment of finite state machines. Master's thesis. – University of Illinois, 1996. – 58 pp.
- Bader D.A. A parallel state assignment algorithm for finite state machines / D.A. Bader, K. Madduri // Proceedings of IEEE Conference on High-Performance Computing. – Bangalore, 2004. – pp. 297-308.
- Sklyarov V. Synthesis and implementation of RAM-based finite state machines in FPGAs / V. Sklyarov // Proceedings of Conference on Field Programmable Logic. – Villach, 2000. – pp. 718-728.
- Barkalov A. Optimization of Moore FSM implemented with CPLD based on PAL macrocells / A. Barkalov, L. Titarenko, S. Chmielewski // Радиотехника. – 2008. – № 155. – pp. 191-195.
- Bukowiec A. State machines synthesis and implementation into FPGAs with multiple encoding of states / A. Bukowiec, A. Barkalov, L. Titarenko // Radioelectronics and Informatics. – 2008. – № 4. – pp. 43-48.
- Czerwinski R. Synthesis of finite state machines for CPLDs / R. Czerwinski, D. Kania // International Journal of Applied Mathematics and Computer Science – Special Section: Robot Control Theory. – 2009. – vol. 19 (4). – pp. 647-659.
- Selvaraj H. FSM implementation in embedded memory blocks of programmable logic devices using functional decomposition / H. Selvaraj, M. Rawski, T. Luba // Proceedings of International Conference on Information Technology: Coding and Computing. – Las Vegas, 2002. – pp. 355-360.
- Barkalov A. Synthesis of Moore finite state machine with nonstandard presentation of state codes / A. Barkalov, L. Titarenko, O. Hebda // Proceedings of KNWS'2010. – Swinoujscie, 2010. – pp. 11-14.
- Perkowski M. Digital design automation – finite state machine design [Электронный ресурс]. – Режим доступа: http://web.cecs.pdx.edu/~mperkows/PerkowskiGoogle/finite-sm.pdf.
- Sentovich E.M. SIS: a system for sequential circuit synthesis / E.M. Sentovich, K.J. Singh, L. Lavagno, C. Moon, R. Murgai, A. Saldanha, H. Savoj, P.R. Stephan, R.K. Brayton, A. Sangiovanni-Vincentelli // Technical Report UCB/ERL M92/41. – Berkley, 1992. – 52 pp.
- Защелкин К.В. Информационная технология автоматизированного проектирования цифровых управляющих устройств / К.В. Защелкин, Е.Н. Иванова // Электромашиностроение и электрооборудование. – 2009. – № 72. – С. 68-72.
- Николенко А.А. Алгоритмические особенности автоматизированного проектирования микропрограммных автоматов / А.А. Николенко, Ю.А. Ковалев, К.В. Защелкин // Электромашиностроение и электрооборудование. – 2000. – № 54. – С. 91-95.
- Полин Е.Л. Абстрактные композиционные автоматы / Е.Л. Полин, К.В. Защелкин // Труды Одесского политехнического университета. – Одесса, 2006. – № 1 (25). – С. 88-94.
- Полин Е.Л. Параллельная модель языка граф-схем алгоритмов и ее интерпретация абстрактными автоматами / Е.Л. Полин, К.В. Защелкин // Электромашиностроение и электрооборудование. – 2005. – № 65. – С. 70-79.
- Полин Е.Л. Язык кластерных граф-схем алгоритмов и основанный на нем метод синтеза цифровых управляющих устройств / Е.Л. Полин, К.В. Защелкин // Электромашиностроение и электрооборудование. – 2008. – № 71. – С. 68-73.
- Vasiltsov I. Evolutionary technique to elementary coding of the internal states of the state machine / I. Vasiltsov // Proceedings of the 2002 NASA/DoD Conference on Evolvable Hardware. – 2002. – pp. 63-64.
- Шувалова Л.А. Структура программного комплекса синтеза и верификации моделей цифровых автоматов / Л.А. Шувалова, Д.Н. Моамар, Т.Ю. Уткина // Системи обробки інформації. – Харьков, 2010. – № 5. – С. 149-152.
- Сердюк С.М. Аналізатор скінченних цифрових автоматів / С.М. Сердюк // Вісник Житомирського державного технологічного університету. – Житомир, 2010. – № 1 (52). – С. 146-151.
- Жабин В.И. Исследование методов построения вычислительных устройств на основе FPGA / В.И. Жабин, Н.А. Ковалев // Технология и конструирование в электронной аппаратуре. – 2002. – № 2. – С. 35-39.
- Опанасенко В.Н. Проектирование и физическая верификация цифровых устройств на ПЛИС / В.Н. Опанасенко, А.Н. Лисовый, Е.В. Сорока // Комп'ютерні засоби, мережі та системи. – 2008. – № 7. – С. 76-85.
- Опанасенко В.М. Формалізація процесу проектування обчислювальних пристроїв та систем на базі ПЛІС / В.М. Опанасенко, О.М. Лісовий // Комп'ютерні засоби, мережі та системи. – 2009. – № 8. – С. 58-63.
- Barkalov A.A. Synthesis of operational and control automata / A.A. Barkalov, L.A. Titarenko. – Donetsk: DonNTU, TechPark DonNTU UNITECH, 2009. – 256 pp.
- Баркалов А.А. Синтез микропрограммных автоматов на заказных и программируемых СБИС / А.А. Баркалов, Л.А. Титаренко. – Донецк: ДонНТУ, Технопарк ДонНТУ УНИТЕХ, 2009. – 336 с.
- Баркалов А.А. Синтез устройств управления на программируемых логических устройствах / А.А. Баркалов. – Донецк: ДонНТУ, 2002. – 262 с.
- Баркалов А.А. Оптимизация схемы МПА Мура на CPLD / А.А. Баркалов, С.А. Ковалев, С.А. Цололо // Материалы Восьмого международного научно-практического семинара «Практика и перспективы развития партнерства в сфере высшей школы». – Донецк-Таганрог, 2007. – Том 3. – С. 26-36.
- Баркалов А.А. Оптимизация логической схемы автомата Мура на FPGA / А.А. Баркалов, А.А. Красичков, С.А. Цололо // Наукові праці ДонНТУ. – Донецк, 2006. – (Серия «Проблеми моделювання та автоматизації проектування динамічних систем»). – № 5 (116). – С. 162-168.
- Баркалов А.А. Оптимизация логической схемы автомата Мура на CPLD / А.А. Баркалов, А.В. Матвиенко, С.А. Цололо // Комп'ютерні засоби, мережі та системи. – 2007. – № 6. – С. 46-51.
- Баркалов А.А. Оптимизация схемы автомата Мура на однородных ПЛИС / А.А. Баркалов, А.В. Матвиенко, С.А. Цололо // Комп'ютерні засоби, мережі та системи. – 2009. – № 8. – С. 45-51.
- Баркалов А.А. Исследование смешанного кодирования состояний для автомата Мура / А.А. Баркалов, В.А. Саломатин, А.А. Красичков, С.А. Цололо // Материалы III научно-практической конференции «Донбас-2020: наука і техніка – виробництву». – Донецк, 2006. – С. 459-562.
- Баркалов А.А. Матричная реализация автомата Мура с кодированием наборов микроопераций / А.А. Баркалов, Р.В. Мальчева, К.А. Солдатов // Наукові праці ДонНТУ. – Донецк, 2010. – (Серия «Проблеми моделювання та автоматизації проектування»). – № 8 (168). – С. 133-143.
- Баркалов А.А. Матричная реализация автомата Мура с расширением кодов состояний перехода / А.А. Баркалов, Р.В. Мальчева, К.А. Солдатов // Наукові праці ДонНТУ. – Донецк, 2010. – (Серия «Інформатика, кібернетика та обчислювальна техніка»). – № 11 (164). – С. 79-83.
- Баркалов А.А. Адаптация MDA для моделирования управляющих автоматов в стандартах UML / А.А. Баркалов, И.Я. Зеленёва, А.А. Гриценко // Радіоелектроніка, інформатика, управління. – Запорожье, 2006. – № 1 (15). – С. 33-37.
- Баркалов А.А. Проектирование и реализация цифровых систем управления с использованием MDA / А.А. Баркалов, И.Я. Зеленёва, А.А. Гриценко // Материалы III научно-практической конференции «Донбас-2020: наука і техніка – виробництву». – Донецк, 2006. – С. 463-467.
- Баркалов А.А. Синтез управляющих автоматов с использованием распределенных и параллельных систем // А.А. Баркалов, И.Я. Зеленёва, А.А. Гриценко // Радіоелектроніка, інформатика, управління. – Запорожье, 2010. – № 1 (22). – С. 128-134.
- Баркалов А.А. Модельно-ориентированный подход к разработке САПР управляющих автоматов / А.А. Баркалов, И.Я. Зеленёва, С.А. Ковалев, А.А. Гриценко // Материалы Пятого международного научно-практического семинара «Практика и перспективы развития партнерства в сфере высшей школы». – Донецк-Таганрог, 2006. – Том 1. – С. 38-43.
- Ковалев С.А. Подход к унификации процесса синтеза МПА Мура для FPGA / С.А. Ковалев, И.Я. Зеленёва, Е.Р. Татолов // Материалы Двенадцатого международного научно-практического семинара «Практика и перспективы развития партнерства в сфере высшей школы». – Донецк-Таганрог, 2011. – Том 2. – С. 45-48.
- XST User Guide for Virtex-4, Virtex-5, Spartan-3, and Newer CPLD Devices [Электронный ресурс]. – Режим доступа: http://www.xilinx.com/support/documentation/sw_manuals/xilinx13_1/xst.pdf.
 Російська
Російська Українська
Українська Англійська
Англійська ДонНТУ
ДонНТУ