Фреймворк для слияния мультисенсорных изображений с использованием графического аппаратного обеспечения

Авторы: Seung-Hun Yoo, Sung-Up Jo, Ki-Young Choi, Chang-Sung Jeong

Источник: http://isif.org/fusion/proceedings/fusion08CD/papers/1569108117.pdf

Перевод с английского: Титаренко К.К.

Аннотация. Данная статья представляет фреймворк для алгоритма слияния мультисенсорных изображений на пиксельном уровне с использованием графического аппаратного обеспечения. Прогресс технологий зондирования способствует максимизации объемов информации, а также повышению требований к производительности процесса слияния. Графические процессоры обеспечивают высокую производительность в сравнении с их ценой и осуществляют быстрые вычисления, поддерживая внутреннюю параллельную обработку - это может быть использовано для увеличения скорости выполнения слияния изображений. На основе результатов реализации методов слияния изображений на пиксельном уровне, используя центральный (CPU) и графический (GPU) процессоры, в данной статье показывается рост по времени выполнения GPU по сравнению со временем выполнения CPU с ростом размерности задачи.

Ключевые слова: слияние мультисенсорных изображений, графический процессор, слияние изображений на пиксельном уровне, параллелизм.

1. Введение

С быстрым развитием производительности GPU и постепенным расширением их программируемости в недавнее время, увеличилась возможность использования GPU для общих нужд, отличающихся от 3D графики [5]. Скорость обработки недавно разработанных GPU значительно превосходит производительность разработанных в аналогичное время CPU. Также, другой тенденцией в разработке GPU является повышение числа программируемых пользователем функций конвейера GPU. Это делает возможным использование GPU для вычислений общего назначения, и, хотя на данный момент ограниченно, GPU может использоваться для целей, схожих с аналогичными для CPU.

С целью улучшения интерпретации данных компьютером или пользователем, слияние изображений быстро продвинулось вперед за несколько последних лет. В результате было разработано множество техник слияния изображений в контексте различных приложений, таких как обнаружение скрытого оружия, дистанционное зондирование, разумные роботы, цифровые камеры, медицинская диагностика, системы наблюдения.

Прогресс технологий зондирования способствует максимизации объемов информации, а также повышению требований к производительности процесса слияния. К примеру, ЭО (электрооптические)/ИК (инфракрасные) авиа снимки, полученные с беспилотных летательных аппаратов, имеют очень высокое разрешение. Требуются существенные объемы памяти и вычислительные мощности, чтобы обеспечить высокоскоростное слияние изображений с высоким разрешением, полученных с нескольких сенсоров [6]. В контексте данной задачи были разработаны специализированные процессоры для слияния изображений и видео реального времени [6] [7]. Но когда используется такое специализированное оборудование, возникают ограничения, такие как недостаточная расширяемость системы из-за дефицита памяти, возрастания цены, модификации алгоритма.

В соответствии с этапом, на котором происходит слияние, алгоритмы слияния изображений могут быть подразделены в зависимости от уровня абстракции: уровень сигнала, уровень пикселей, уровень особенностей и уровень символов. На данный момент большинство приложений слияния изображений задействует методы, работающие на пиксельном уровне. При слиянии на пиксельном уровне, входные изображения комбинируются, рассматривая отдельные значения пикселей, либо небольшого окна, отцентрированного в текущей пиксельной позиции, или же специальные регионы. Следует заметить, что эти алгоритмы также легки в реализации.

Большинство алгоритмов слияния изображений требуют SIMD-подхода. Эта статья представляет базирующийся на GPU фреймворк для высокоскоростного слияния мультисенсорных изображений, а также показывает увеличение скорости обработки в сравнении с CPU. Реализованы алгоритмы слияния на уровне пикселей, такие как взвешенное среднее, PCA, пирамида Лапласа, дискретное вейвлет-преобразование (DWT), а также определено время их выполнения в соответствии с нашими экспериментами. Реализация этих алгоритмов осуществлена с использованием таких техник, как «Render-To-Texture» (RTT, рендеринг в текстуру) и «Multi-Pass Rendering» (MPR, многопроходный рендеринг) для быстрого исполнения на фрагментном процессоре GPU [4] [13] [17].

Данная статья организована следующим образом. Вначале рассматривается архитектура, а также модель программирования GPU в разделе 2, затем, в разделе 3, описываются алгоритмы слияния на пиксельном уровне. В разделе 4 обсуждается структура фреймворка для высокоскоростного слияния изображений, а также процесс его реализации на GPU. В разделе 5 осуществляется сравнение производительности путем замера скорости исполнения методов слияния, реализованных на CPU и GPU, раздел 6 завершает нашу работу.

2. Графический процессор

GPU – это специализированное устройство для рендеринга графики, которое ускоряет генерацию 3D сцены. С простой и параллельной архитектурой, скорость вычислений последних GPU, по крайней мере, в 3-4 раза выше, чем CPU и разрыв между GPU и CPU увеличивается. В частности, велики преимущества использования значительной вычислительной мощности и скорости SIMD архитектуры GPU, причем в то же время CPU может быть загружен другими задачами [4]. В данном разделе мы кратко представим архитектуру и модель программирования GPU.

А. Графический конвейер

Конструкция графических процессоров традиционно следовала общей структуре, известной как графический конвейер [4] [5] [13] [14] [15]. Данный конвейер сконструирован для того, чтобы позволить аппаратному обеспечению обеспечивать высокие темпы вычислений путем параллельного исполнения. Он делится на три основных этапа: обработка геометрии, растеризация, обработка фрагментов. На вход подается список геометрии, представленный вершинами в координатах объекта; на выходе конвейера – изображение в фреймбуфере. В аппаратном обеспечении каждый этап реализован как отдельный блок на GPU. Упрощенный графический конвейер (на данное время) показан на рис. 1.

Рис. 1 – Графический конвейер

Графический конвейер позволяет использовать многоуровневый параллелизм, что приводит к высоким темпам вычислений и высокой пропускной способности [15] [16]. Каждый из этапов обычно реализован как отдельный компонент аппаратного обеспечения, что позволяет перекрывать исполнение каждой задачи (т. е. обеспечивать параллелизм на уровне задач). В дополнение, конвейер состоит из нескольких вершинных и фрагментных (пиксельных) процессоров, позволяющих выполнять множество параллельных на уровне данных операций над данным набором входных вершин и результирующих пикселей (т. е. обеспечивать параллелизм на уровне данных). К примеру, распространенные конструкции аппаратного обеспечения используют 6-8 вершинных процессоров и 32-48 фрагментных процессоров. Более того, в процессе обработки одного элемента, мы можем использовать параллелизм на уровне инструкций. В то время, когда ранние реализации графического конвейера базировались полностью на конструкции с фиксированным набором функций, несколько последних поколений предоставили возможность программирования соответствующих функций пользователем. Как показано на рис. 1, программисты могут писать код как для вершинных, так и для фрагментных процессоров. Каждая программа обычно использует ограниченное число доступных входных и выходных параметров, регистров, констант, и общего количества инструкций. Входными параметрами для программ могут быть скалярные значения, двух-, трех- или четырехкомпонентные векторы, массивы значений (скалярных или векторных), которые хранятся в текстурной памяти видеокарты.

Б. Модель программирования GPU

Вычисления общего назначения на GPU порождают проблемы даже для задач, которые хорошо отражаются на GPU, поскольку, не смотря на продвижение в вопросах программируемости и высокоуровневых языков, графическое аппаратное обеспечение остается достаточно сложным для использования с целью решения неграфических задач.

Мы описываем потоковую модель программирования, которая является базисом при программировании GPU сегодня. При потоковой модели программирования все данные представляются как поток, который определяется как упорядоченное множество данных одного типа, тогда как ядра – маленькие программы – оперируют потоками. Ядра берут поток как исходные данные и производят поток как результат. Как показано на рис. 1, графический конвейер структурирован по этапам вычислений, соединенных потоком данных. Эта структура аналогична абстракциям «ядро» и «поток» потоковой модели программирования. Потоковая модель программирования на GPU предлагает SIMD-базированные вычислительные возможности.

Типичная программа общего назначения на GPU использует фрагментный процессор, поскольку программируемым этапом с максимальным темпом арифметических вычислений является именно он. Фрагментные процессоры имеют возможность извлекать данные из текстур, поэтому они способны производить сбор данных (gather). Тем не менее, выходной адрес фрагмента всегда определяется перед тем, как фрагмент обрабатывается, отсюда процессор не может изменить расположение выходного пикселя, поэтому фрагментные процессоры не способны выполнять рассеяние данных (scatter). Программисты должны прибегать к различным трюкам, чтобы достичь выполнения операции «scatter». Модель программирования GPU имеет множество качеств, позволяющих достичь увеличения производительности, но в то же время существует достаточно ограничений при программировании приложения общего назначения.

Особенно, модель программирования GPU имеет преимущества и недостатки в различных сторонах доступа к памяти. К примеру, содержимое памяти фреймбуфера может быть отображено или записано в текстурную память, этот процесс называется «рендер в текстуру». Он реализует непосредственную обратную связь выхода GPU со входом без обращения к CPU, что ведет к повышению эффективности. С другой стороны, фрагментный процессор не может использовать непрямую адресацию памяти при операции записи, а также использовать одну и ту же память как вход и выход.

Шейдерные языки прямо нацелены на программирование этапов графического конвейера. Наиболее известные из них – это Cg, OpenGL Shading Language и High-Level Shading Language от Microsoft. Cg («C для графики») [21] является высокоуровневым шейдерным языком, разработанным компанией NVIDIA, его синтаксис и семантика очень похожи на язык программирования C. Большинство наших методов слияния реализованы на GPU с использованием Cg и OpenGL с графическим пользовательским интерфейсом.

3. Методы слияния изображений на пиксельном уровне

Методы слияния на пиксельном уровне могут быть приблизительно подразделены на две группы: методы слияния в градациях серого и методы слияния в цвете [1] [3] [12]. Методы слияния в градациях серого подразделяются на базирующиеся на многомерном разложении (multi-scale-decomposition-based, MDB) и остальные (non-multi-scale-decomposition-based, NMDB). Методы слияния в цвете подразделяются на методы, работающие с истинным (true-color) и псевдоцветом (false-color). Некоторые характерные алгоритмы, такие как взвешенное усреднение, пирамида Лапласа, DWT, TNO, рассмотрены в данном разделе.

А. Взвешенное среднее

Вероятно, самый прямолинейный метод слияния изображений с разных сенсоров - это выполнить слияние как взвешенную суперпозицию входных изображений.

F(i, j) = w1*I1(i, j) + w2*I2(i, j),

где w1 и w2 – коэффициенты, I1(i, j) и I2(i, j) – значения пикселей исходных изображений. Простой подход к определению коэффициентов состоит в построении результата с применением простого нелинейного оператора, такого как минимум или максимум. Также оптимальные коэффициенты могут быть получены путем применения анализа главных компонент (principal component analysis, PCA) ко всем входным множествам значений интенсивности [3] [12]. Использование PCA в основе ограничено использованием глобальной дисперсии как меры значимости и всегда будет приводить к получению более высокого коэффициента для входного изображения с большей дисперсией.

Б. Пирамида Лапласа

Пирамиды изображений были изначально описаны для анализа изображений с мультиразрешением как модель для бинокулярного слияния в человеческом зрении [18]. Пирамиды изображений с мультиразрешением строятся последовательной фильтрацией и снижением разрешения исходного изображения. Ввиду снижения разрешения, размер изображения делится вдвое в обоих пространственных направлениях на каждом уровне процесса декомпозиции, что ведет к представлению сигнала в мультиразрешении. Несколько базирующихся на пирамиде схем были предложены за последние годы. Здесь приводится только пирамида Лапласа ввиду того, что она показала наиболее высокую производительность среди всех пирамид [18] [19]. Каждый уровень пирамиды Лапласа рекурсивно строится на основе ее нижнего уровня, применяя следующие четыре базовых шага: размытие (низкочастотное фильтрование); снижение разрешения; интерполяция (расширение); и вычитание (двух изображений попиксельно) [20]. Детализированные изображения, полученные в ходе операции вычитания, сливаются, используя правило выделения максимума в каждой точке, и затем комбинируются в то же изображение из нижнего уровня пирамиды.

В. Дискретное вейвлет-преобразование

Общая техника вейвлет-преобразования, использующаяся для слияния – это DWT (discrete wavelet transform) [9] [14]. 1D DWT вовлекает последовательное фильтрование и понижение разрешения сигнала. Для изображений 1D DWT используется в двух измерениях путем раздельного фильтрования и понижения разрешения в горизонтальном и вертикальном направлениях. Это дает четыре субканала на каждом уровне преобразования с чувствительностью к вертикальным, горизонтальным и диагональным частотам. Коэффициенты DWT для двух сливаемых изображений подвергаются операции слияния (попиксельно), выбирая среднее коэффициентов приближения на самом высоком уровне преобразования и самое большое абсолютное значение детальных коэффициентов на каждом уровне преобразования. Далее выполняется обратное DWT для получения слитого изображения. Следует отметить, что у данного метода были найдены некоторые преимущества над пирамидальными методами, такие как увеличение информации по направлениям [1]; отсутствие блокирующих артефактов, которые часто возникают в изображениях, слитых с помощью пирамидальных методов; лучшее отношение сигнал-шум; улучшенное восприятие человеком, отмеченное в ходе соответствующего анализа.

Г. TNO

Слияние в цвете может состоять из присвоения двух исходных изображений трем плоскостям RGB-изображения. Toet предложил простое улучшение базовой схемы слияния в RGB цвете, которое стало известно как метод TNO [11]. В этом методе вычисляется общая компонента, определенная как пиксель с минимальным значением для каждой пары пикселей двух изображений. Это значение вычитается из обоих изображений для того, чтобы оставить уникальную информацию в каждом. Эти уникальные компоненты из каждого противоположного изображения удаляются из каждого из исходных изображений, после этого результирующие изображения присваиваются как красный и зеленый каналы слитого изображения.

4. Фреймворк для слияния изображений

В этом разделе описывается предложенный фреймворк для слияния мультисенсорных изображений, используя GPU и объясняется как алгоритмы слияния на пиксельном уровне были реализованы на GPU.

А. Предложенный фреймворк

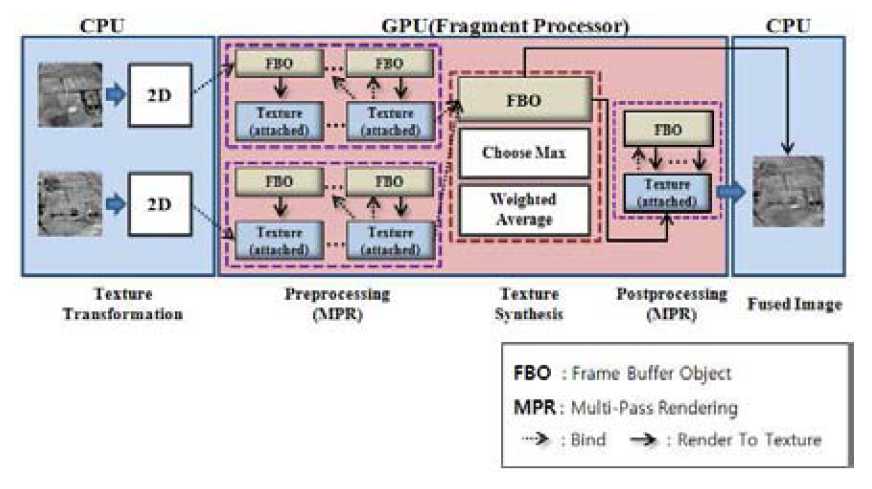
Рис. 2 – Предложенный фреймворк для слияния мультисенсорных изображений с использованием графического аппаратного обеспечения

На рис. 2 показан предложенный фреймворк для слияния мультисенсорных изображений с использованием GPU. Этот фреймворк примерно делится на четыре этапа: преобразование текстуры, предварительная обработка, синтез текстуры и постобработка. На этапе преобразования текстуры выполняется операция, которая конвертирует 8-битное серое или 24-битное цветное входное изображение в 2D текстуру, к которой может быть применен процесс слияния, исполняющийся фрагментными процессорами. После конверсии в текстуру производится ее загрузка в текстурную память в соответствии с функциями OpenGL. Текстуры в текстурной памяти используются как вход для фрагментных программ, выполняемых фрагментными процессорами. Выходом данного процесса является иная текстурная память, прикрепленная к FBO (фреймбуферу). Этот процесс называется «Render-To-Texture», он позволяет организовать обратную связь, посылая выход фрагментной программы обратно в текстурную память вместо вывода в фреймбуфер, что делается по умолчанию. Каждая фрагментная программа представляет один проход многопроходной схемы вычислений на GPU. Отсюда использование техники «Multi-Pass Rendering» (MPR, многопроходный рендеринг) для выполнения многофрагментных программ алгоритмов слияния. Все процессы, исполняющиеся в фрагментных процессорах для слияния изображений, используют RTT структуру, и слияние может выполняться на высокой скорости путем использования MPR с целью исполнения более одной фрагментной программы, что необходимо для процедур пре- и постобработки.

Б. Реализация на GPU

Далее кратко изложена реализация всего процесса. Вначале записывается каждая из функций, используемых алгоритмами, в фрагментную программу и входные изображения сохраняются в текстурной памяти. Каждая фрагментная программа исполняется фрагментным процессором, и результирующие изображения вновь сохраняются в текстуре. Рис. 3. Иллюстрирует структуру каждой фрагментной программы на каждом этапе фреймворка для четырех типов алгоритмов слияния на пиксельном уровне, рассмотренных в разделе 3. Часть, отмеченная скругленным прямоугольником, представляет собой фрагментную программу, стрелка же представляет ввод/вывод текстуры.

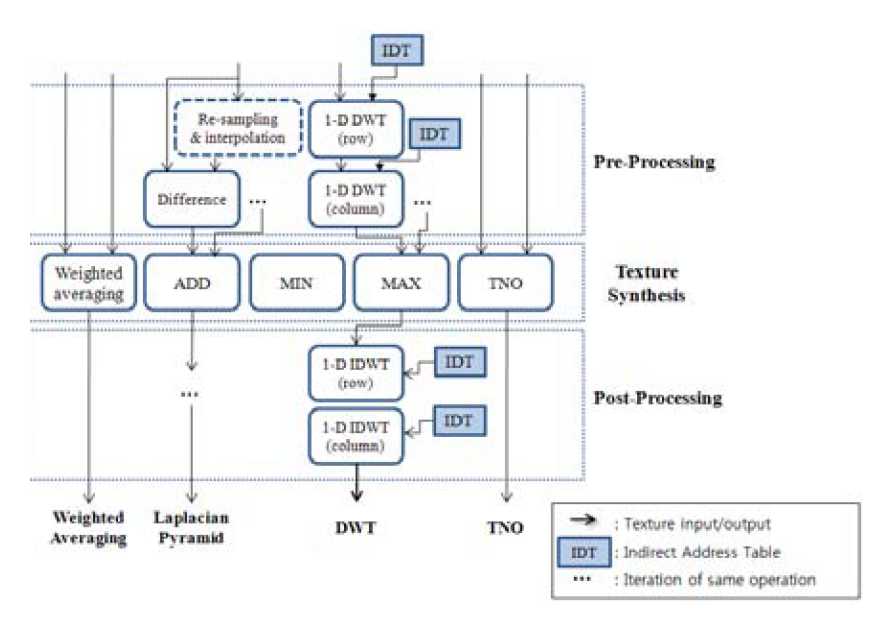
Рис. 3 – Структура каждой фрагментной программы по этапам фреймворка

Рассматривая алгоритмы по отдельности, взвешенное усреднение и метод TNO состоят из единственной фрагментной программы, получающей на вход 2 текстуры и генерирующей синтезированную текстуру.

Рис. 4 – Пример фрагментной программы на Cg. Взвешенное усреднение (слева) и TNO (справа)

Рис. 4 иллюстрирует пример, реализованный с помощью использования Cg. В случае алгоритма пирамиды Лапласа операции reduce/expand были выполнены с помощью ресамплинга и интерполяции, поддерживаемых OpenGL. Также, с увеличением уровня пирамиды, структуры, показанные на рис. 3, примут более сложную форму. В случае синтеза с помощью алгоритма DWT, базирующийся на свертке DWT был реализован на GPU. На каждом уровне 2D DWT достигается путем исполнения 1D DWT сначала горизонтально и затем вертикально. Для вычисления произведений и сумм, необходимых при каждом процессе рендеринга DWT/IDWT, должна быть составлена и использована как входная текстура для фрагментной программы таблица непрямой адресации в соответствии с методом, предложенным J. Wang [5].

5. Эксперименты

Для определения производительности на GPU алгоритмов слияния на пиксельном уровне скорость выполнения слияния была замерена путем исполнения реализации каждого из вышеупомянутых 4 типов алгоритмов на CPU и GPU, а также изменения разрешения изображений. В случае метода взвешенного среднего, значение веса было выбрано равным 0.5, после чего была замерена скорость исполнения реализации. В случае методов пирамиды Лапласа и DWT была выполнена классификация по уровням 1 и 3, после чего был произведен замер скорости. Тест был проведен в среде с использованием Intel Core2 CPU 6600 2.4GHz и NVIDIA Geforce 8600 GTS GPU. Как стандарт в измерении скорости, скорость слияния была вычислена, исключая время инициализации и конфигурации OpenGL и Cg.

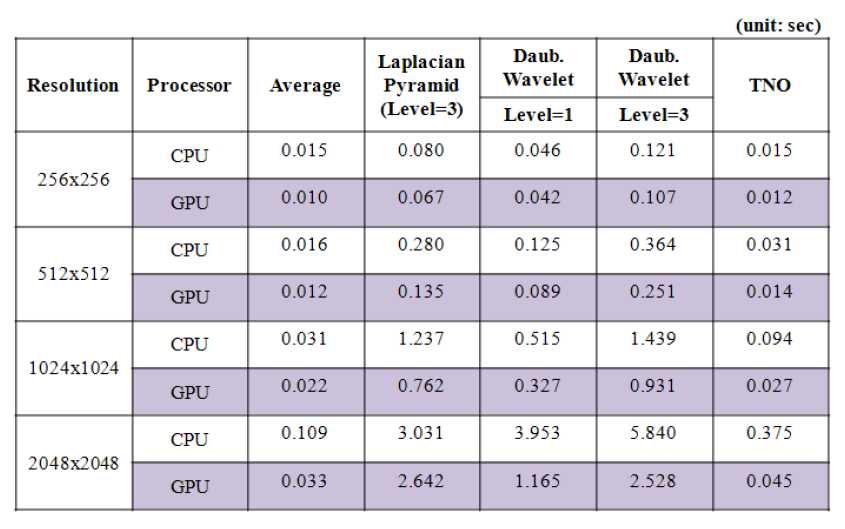
Рис. 5 – Время выполнения слияния изображений

На рис. 5 показано время, замеренное для каждого из алгоритмов слияния для каждого из разрешений. Сравнительно с различными методами слияния, метод взвешенного среднего имеет самую простую и быструю реализацию. Данный метод, который практически не требует оптимизации реализации, ясно показывает различия в производительности обеих процессоров (CPU и GPU). Разница в скорости в более чем 30% показывает отличие в производительности, достигнутое благодаря тому, что были задействованы 128 фрагментных процессоров GPU, исполняющих единственную фрагментную программу, чему противопоставлено исполнение на одном процессоре на CPU. Метод слияния с мультиразрешением показывает рост по времени выполнения GPU по сравнению со временем выполнения CPU с увеличением уровня и разрешения.

6. Заключение

В последнее время GPU массового рынка стали использоваться не только для рендеринга 3D графики, но и для вычислений общего назначения (GPGPU) в виду увеличения соотношения цена/производительность продукта и программируемости аппаратного обеспечения, так же как и значительной вычислительной мощности и скорости GPU. Алгоритмы слияния изображений на пиксельном уровне исполняются на большом объеме данных, обрабатываемых одной и той же командой. Также, ввиду возрастания важности слияния изображений с высоким разрешением и высокой скоростью, с развитием технологий зондирования, слияние изображений с использованием GPU оказывается правильным решением. Эта работа представила фреймворк для слияния изображений на пиксельном уровне с использованием GPU, в ней также была получена реализация базовых актуальных алгоритмов слияния для CPU и GPU для сравнения производительности. Как результат, было продемонстрировано улучшение скорости исполнения на более чем 30% в сравнении с CPU благодаря параллелизму на уровне данных, задач и инструкций, предоставляемых конструкцией и программной моделью GPU, в том числе благодаря реализации техник, использующих рендеринг в текстуру и многопроходный рендеринг. В будущем, планируется достичь большей эффективности процесса слияния с использованием CUDA и видеокарт следующего поколения от NVIDIA, которые сделают возможным использование более широких возможностей работы с памятью, которые могут применяться для значительного числа алгоритмов слияния изображений, находящихся в настоящее время в развитии.

Благодарности

Это исследование велось при поддержке MIC (Ministry of Information and Communication), Корея, по программе ITRC (Information Technology Research Center) под руководством IITA (Institute of Information Technology Assessment), Brain Korea 21 Projects в 2008 и Seoul Forum for Industry- University-Research Cooperation.

Ссылки

[1] Yang, Yi Han, Chongzhao Kang, Xin Han, Deqiang, “An Overview on Pixel-Level Image Fusion in Remote Sensing”, IEEE conference, Automation and Logistics, pp.2339-2344, Aug. 2007.

[2] Gemma Piella, “A general framework for multiresolution image fusion: from pixel to regions”, Information Fusion, pp.259-280,2003.

[3] M. Smith and J. Heather, “Review of image fusion technology in 2005”, www.waterfallsolutions.co.uk, 2005.

[4] John D. Owens, David Luebke, “A Survey of General-Purpose Computation on Graphics Hardware”, in Eurographics 2005, State of the Art Reports, pp.21-51, August 2005.

[5] T. T. Wong, C. S. Leung, P. A. Heng and J. Wang, “Discrete Wavelet Transform on Consumer-Level Graphics Hardware”, IEEE Transactions on Multimedia, Vol. 9, No. 3, pp.668-673, April 2007.

[6] A.Ardeshir Goshtasby, Guest Editors and Stavri Nikolov, “Image Fusion: Advances in the State of the Art”, Information Fusion, Vol. 8, issue 2, pp.114-118, April 2007.

[7] Fay, D. Ilardi, P. Sheldon, N. Grau, D. Biehl, R. Waxman, A, “Realtime image fusion and target learning & detection on a laptop attached processor”, Information Fusion, International Conference, 2005.

[8] Nolan Godnight, Rui Wang, and Greg Humphreys, “Computation on Programmable Graphics Hardware”, IEEE Computer Graphics and Applications, 2005.

[9] G.Pajares and J.M.de la Cruz, “An wavelet-based image fusion tutorial,” Pattern Recognition, 37, pp.1855-1872 2004.

[10] http://www.nvidia.com/dev content/nvopenglspecs/GL EXT framebuffer object.txt

[11] A. Toet, J.J. Van Ruyven, J.M. Valeton, “Merging thermal and visual images by a contrast pyramid”, Optical Engineering 28 (7), pp.789-792, 1989.

[12] Rick S. Blum and Zheng Liu, Multi-Sensor Image Fusion and Its Applications. Taylor & Francis, CRC Press, July 2005.

[13] J. L. Cornwall, “Efficient multiple pass, multiple output algorithms on the GPU”, in 2nd European Conference on Visual Media Production pp.253-262, 2005.

[14] C. Tenllado, J. Setoain, M. Prieto, L. Pinuel, F. Tirado, “Parallel implementation of the 2D Discrete Wavelet Transform on Graphics Processing Units: Filter-Bank versus Lifting, IEEE Transaction on Parallel and Distributed Computing versus Lifting”, IEEE Transactions on Parallel and Distributed Computing(Magazine), 2008.

[15] Matt Pharr, Randima Fernando, GPU Gems 2: Programming Techniques for High-Performance Graphics and General-Purpose Computation. Addison Wesley.

[16] P.S. McCormick, J. Inman, J.P. Ahrens, C. Hansen, G. Roth, “Scout: A hardware-accelerated system for quantitatively driven visualization and analysis”, in Proceedings of IEEE Visualization, pp. 171.178, 2004.

[17] James Fung, Steve Mann, “Computer Vision Signal Processing on Graphics Processing Units”, Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), 2004.

[18] Y. Zheng, E. A. Essock, B. C. Hansen, and A. M. Haun, “A new metric based on extended spatial frequency and its application to DWT based fusion algorithms”, Information Fusion 8, pp.177-192, 2007.

[19] Y. Zheng, E.A. Essock, B.C. Hansen, “An advanced image fusion algorithm based on wavelet transform incorporation with PCA and morphological processing”, Proc. SPIE 5298 pp.177-187, 2004.

[20] P.J. Burt, E. Adelson, “The Laplacian pyramid as a compact image code, IEEE Trans. Commun”. IEEE Transactions on Communications pp.532-540, 1983.

[21] Randima Fernando, Mark J. Kilgard, The Cg Tutorial: The Definitive Guide to Programmable Real-Time Graphics. Addison Wesley.