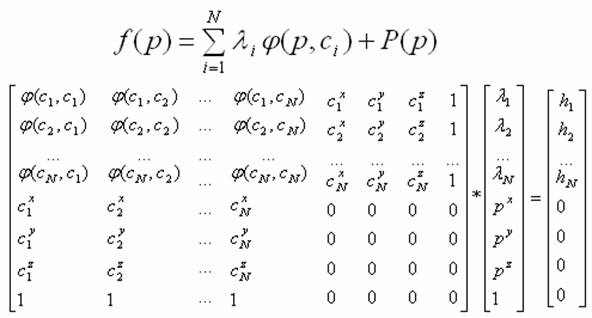Решение задачи
построения изоповерхностей на базе CPU и GPU

 

                             Титаренко К.К.

                             рук. Бабков В.С.

 

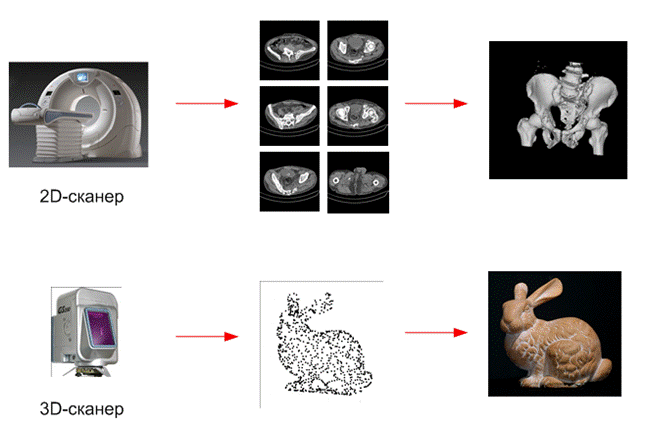
Источники исходных данных

Математическая постановка задачи

Обеспечение нетривиальности решения

 

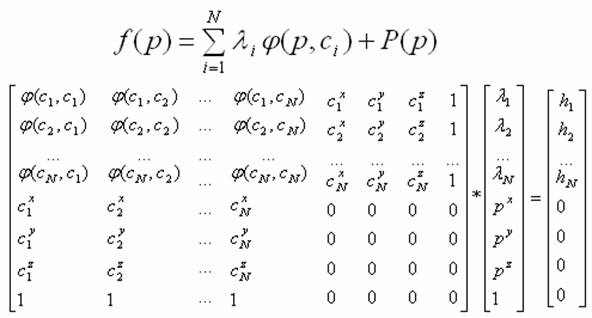
Методы решения СЛАУ

 

Рассматриваемые:

•       прямые: LDLT

•       итерационные: Якоби

 

Реализации:

•       LDLT-CPU

•       LDLT-CPU-MT

•       LDLT-CUDA

•       LDLT-CUDA-2

•       JACOBI-CUDA

 

Кратко о CUDA

 

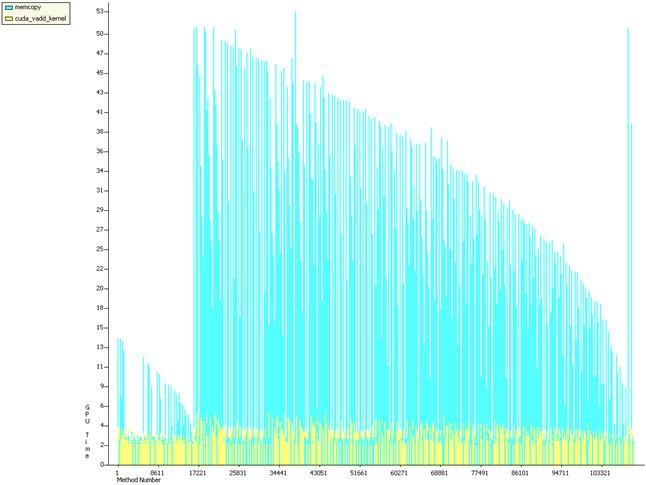
LDLT-CUDA, LDLT-CUDA-2

 

LDLT-CUDA-2: хронология использования GPU

 

 

LDLT-CUDA, LDLT-CPU

LDLT-CUDA: хронология использования GPU

 

LDLT-CPU, JACOBI-CUDA

 

 

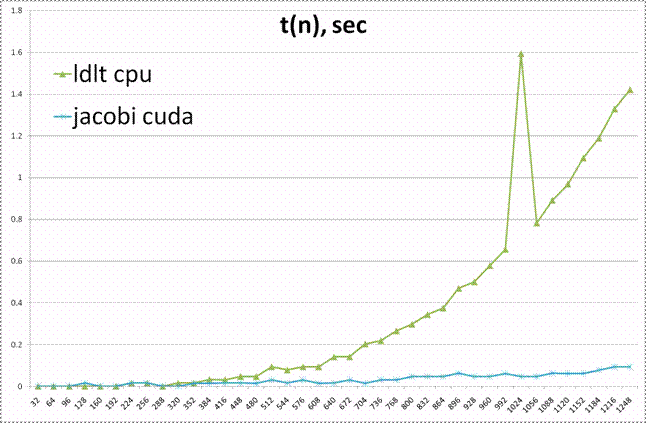
LDLT-CPU, JACOBI-CUDA

 

 

Выигрыш в производительности (в разах) при использовании JACOBI-CUDA над LDLT-CPU

 

 

Максимальная ошибка

 

 

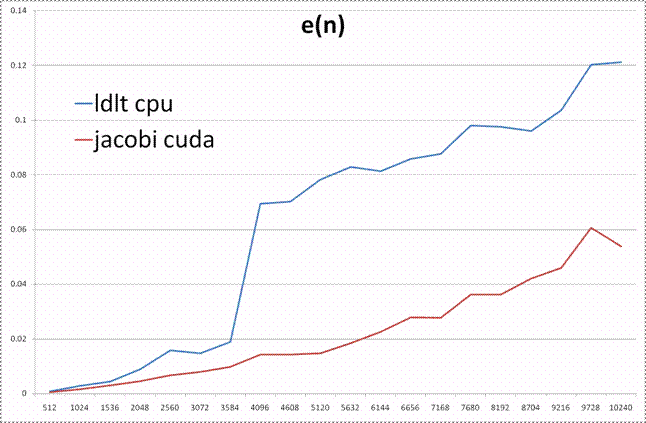
Выводы

 

Эффективная реализация возможна:

•       GPU: итерационные методы

•       CPU: прямые методы

 

 

Стоит рассмотреть:

•       Возможные модификации исходной СЛАУ

•       Итерационные методы, для которых выполняются условия сходимости для исходной СЛАУ