ОПТИМИЗАЦИЯ ВЫПОЛНЕНИЯ РАСПРЕДЕЛЁННЫХ ЗАПРОСОВ
Заславский В.А., Савкова Е.О.
Донецкий Национальный Технический Университет
кафедра автоматизированных систем управления
E-mail: bobah22@gmail.com
Аннотация:
Заславский В.А., Савкова Е.О. Оптимизация выполнения распределённых
запросов. Рассмотрена проблема оптимизации запросов в распределённых системах.
Описаны подходы к оптимизации запросов, общий вид процесса оптимизации.
Рассмотрены алгоритмы формирования альтернативных глобальных планов выполнения распределённых
запросов и выбора наиболее эффективного из них.
Актуальность задачи
SQL-ориентированные базы данных активно используются во многих современных приложениях. Проблема оптимизации запросов особо остро стоит в контексте популярных веб-базированных систем, т.к. количество их пользователей может исчисляться в миллионах человек. В таких условиях оптимизация SQL-запросов выходит на первый план: скорость выполнения запросов определяет производительность всех вышестоящих процедур, и таким образом, оптимизация других компонентов системы лишена смысла, если не была предварительно проведена оптимизация используемых запросов.
Также количество пользователей системы определяет и принцип распределённой организации данных: во-первых, для своевременной обработки такого количества запросов не хватает мощности одного сервера; во-вторых, существует проблема недостатка в дисковом пространстве для хранения данных, т.к. крупная система помимо оперативной информации должна хранить «журнальные» данные о сессиях, ошибках, и так далее. Таким образом, распределённая модель хранения данных является неотъемлемой частью крупного приложения, и распределённые запросы также должны быть должным образом оптимизированы.
Общая постановка задачи
Задача оптимизации запроса заключается в нахождении
оптимального способа его выполнения. Выбор способа осуществляется на основании
набора альтернативных планов выполнения, каждый из которых является вариантом
перестановки таблиц, к которым происходит обращение. Оптимизация запросов
производится в двух целях: минимизация времени и ресурсов, которые нужно
затратить на выполнение запроса и максимизация количества обслуживаемых
клиентов. Задачу оптимизации запросов
можно разделить на три подзадачи:
1.
Логическая
оптимизация - преобразование логических элементов запроса к наиболее
оптимальному представлению.
2.
Формирование набора
планов выполнения запроса.
3.
Оценка
сформированных планов и выбор наиболее оптимального из них.
Набор ресурсов, который подлежит минимизации, состоит из таких компонентов:
1. Затраты на передачу данных между клиентом и сервером. Они линейно зависят от объёма передаваемых данных, а так же от качества и пропускной способности канала.
2. Время загрузки страниц в память компьютера. Зависит от объёма данных и скорости устройств.
3. Загрузка процессора при выполнении вычислений [1].
В зависимости от соотношения этих компонентов нужно выбрать способ оптимизации. Для баз данных, распределённых между несколькими серверами, наиболее важным ресурсом являются затраты на коммуникацию. Таким образом, алгоритм оптимизации запросов для распределённых баз данных будет базироваться именно на этом параметре.
Выбор подхода к оптимизации запросов
Существует два базовых подхода в оптимизации запросов: нисходящий и восходящий, которые реализуют принципы «от общего к частному» и «от частного в общему» соответственно [2].
Восходящий подход характерен изучением особых частных случаев и их оптимизацией с последующим «строительством» из них более крупных элементов. Этот подход эффективен в тех случаях, когда стоит задача оптимизации известного статического набора запросов.
Нисходящий
подход более глобален и универсален, т.к. он действует в эвристической манере.
Он эффективен для оптимизации работы системы вообще, когда статического набора
запросов не существует, а множество возможных запросов велико. Для поиска
оптимального глобального плана выполнения распределённого запроса мы выберем
именно этот подход. Общий вид алгоритма нисходящего подхода представлен на
рисунке 1.
Рисунок 1 – Общий вид процесса оптимизации
Рассмотрим подробнее последний шаг оптимизации –
формирование и выбор оптимального плана. Во-первых, для эффективной работы
этого шага необходимо наличие дополнительной базы данных, содержащей
необходимую исходную информацию (так называемой «метабазы»),
такую как:
·
Структура базы данных,
работа с которой оптимизируется;
·
Распределение
содержимого таблиц по серверам (этот пункт особо важен для распределённых баз
данных);
·
Статистика запросов, и
так далее.
Во-вторых, необходимо выбрать такой алгоритм, чтоб сумма
стоимостей его выполнения и выполнения выбранного плана запроса была меньше,
чем стоимость выполнения неоптимизированного плана запроса. Другими словами,
для задачи формирования и выбора глобального плана распределённого запроса при
небольшом количестве серверов и простоте распределения данных, наиболее
оптимальным алгоритмом является полный перебор. При увеличении количества
серверов появляется потребность в выборе менее затратного алгоритма. Также это
усугубляется необходимостью «интеллектуального» распределения данных на
основании статистической информации.
Выбор алгоритма
оптимизации
В настоящий момент в оптимизаторах распределённых запросов
наиболее распространены полный перебор (стратегия грубой силы) и генетический алгоритм.
В первом случае исследуются все сочетания выбираемых таблиц в поиске наименее
затратного.
Во втором случае все выбираемые таблицы кодируются в
хромосомы, для которых запускается механизм естественного отбора (операторы
селекции, скрещивания, мутации) в соответствии с заданной функцией стоимости. В
качестве хромосомы здесь выступает представление запроса в виде
последовательности элементарных операций в форме дерева [3]. Рассмотрим этот способ кодирования
хромосомы на примере элементарного выражения:
(a or b) and (c or d)
Для этого выражения можно построить дерево, представленное
на рисунке 2.
Рисунок 2 – Древовидное представление запроса
В процессе логической оптимизации
создаётся большое количество различных вариантов представления запроса в виде
набора элементарных операций. Каждый из этих вариантов представляется в виде
дерева. В процессе работы оператора скрещивания деревья обмениваются между
собой своими ветвями, и в результате остаётся наиболее оптимальный вариант. Для
задачи поиска глобальных планов распределённых запросов используется
аналогичный принцип.
Генетический алгоритм исследует не всё множество возможных
вариантов, поэтому он не всегда находит глобальный оптимум, и оптимизация
запроса в этом случае проявляется в виде «оптимизации алгоритма оптимизации».
В качестве альтернативного алгоритма было предложено
представить процесс выбора оптимального плана запроса в виде графа. Для этого
сначала нужно разделить всю запрашиваемую информацию на группы (например, по
таблицам; назовём это классами), после чего выяснить, на каких из серверов БД
хранятся эти группы. Эта информация будет исходной для построения графа. Пример
таблицы представлен в таблице 1.
Таблица
1. Исходные данные для построения графа.
|
Сервер |
Классы |
|
1 |
2,3 |
|
2 |
1,2 |
|
3 |
3 |
На основании полученных данных можно построить граф,
который представлен на рисунке 3. Индекс каждой вершины графа обозначает номер
сервера, к которому возможно отправить запрос для получения части нужных
данных. Вершина «Start»
соответствует входному значению запроса, «End» – наиболее оптимальный план.
Каждое ребро графа имеет вес, который вычисляется функцией, входными
параметрами которой могут быть текущая загруженность сервера, полоса
пропускания канала, и так далее.
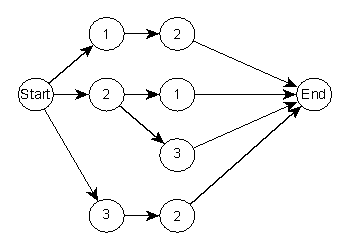
Рисунок 3 – Процесс оптимизации запроса в виде графа
Таким
образом, задача поиска оптимального плана распределённого запроса сводится к
задаче поиска кратчайшего пути на графе, которая может быть решена муравьиным
алгоритмом.
Решение задачи поиска оптимального плана
Приведём пример решения поставленной задачи. В качестве исходных данных будем использовать таблицу, приведённую выше, дополненную весом для каждого сервера. Чем больше вес – тем более затратно проходит работа с этим сервером. Модифицированная таблица исходных данных представлена в таблице 2.
Таблица
2. Исходные данные для построения графа с учётом весов.
|
Сервер |
Классы |
Вес |
|
1 |
2,3 |
3 |
|
2 |
1,2 |
2 |
|
3 |
3 |
1 |
Дополним граф, представленный на рисунке 3 нужной информацией: индекс каждой вершины заполним в виде [<Порядковый номер>: S<Номер сервера>], а так же отметим веса вершин (рисунок 4).
Рисунок 4 – Граф распределённого запроса
Результат очевиден: наиболее оптимальным набором серверов (при котором сумма весов вершин минимальна) являются серверы 3 и 2.
Выводы
В процессе работы был изучен ряд вопросов, касающихся оптимизации запросов к базам данных. В результате было выяснено, что процесс обработки запроса состоит из нескольких стадий, наиболее важной из которых с точки зрения оптимизации распределённых запросов является выбор альтернативного плана. Было предложено представить процесс оптимизации в виде графа и использовать муравьиный алгоритм для поиска оптимального пути по нему.
Литература
1.
Матиас Ярке, Юрген Кох. Оптимизация
запросов в системах баз данных
//
Computing Surveys, Vol. 16, No. 2, June 1984.
2.
Гребенников Н.
А. Метод поиска оптимального плана выполнения запросов к базам данных на основе
нисходящей стратегии.
3.
Suhail S. J. Owais, Pavel
Kromer, Vaclav Snasel.
Query Optimization by Genetic Algorithms с. 128.