АППАРАТНАЯ РЕАЛИЗАЦИЯ И КОРРЕКТИРУЮЩИЕ ВОЗМОЖНОСТИ КОДОВ РИДА-СОЛОМОНА
Дяченко
О.Н.
Донецкий национальный технический
университет
do@cs.donntu.ru
Abstract
Dyachenko O.N. Hardware
implementation and correcting possibilities of Reed-Solomon codes. Integrated assessment of modes of hardware implementation for encoders and decoders for Reed-Solomon codes is discussed. Analysis of choice of generator
polynomial is concerned using single-error-correcting Reed-Solomon code as
example; characteristic properties of construction of code and circuits
of encoder and decoders are illustrated. Method of increase of correcting
possibilities of codes is proposed.
Введение
Коды
Рида-Соломона нашли широкое применение в цифровых системах связи и хранения
информации. Можно привести несколько наиболее известных примеров: (255, 223,
33) код Рида-Соломона для космической связи NASA, укороченные коды Рида-Соломона
над полем Галуа GF(28)
для CD-ROM, DVD и цифрового телевидения высокого
разрешения (формат HDTV),
расширенный (128, 122, 7) код Рида-Соломона над полем Галуа GF(27) для кабельных модемов [1]. Коды Рида-Соломона широко
описаны в литературе [1, 2, 3], но вместе с тем аппаратная реализация
кодирования и декодирования освещена либо вкратце, либо вовсе отсутствует.
Данная работа посвящена особенностям построения кодирующих и декодирующих
устройств кодов Рида-Соломона и их корректирующих возможностей.
1. Порождающий полином
кодов Рида-Соломона
Коды
Рида – Соломона являются частным случаем кодов БЧХ. Главное отличие кодов Рида
– Соломона заключается в том, что в качестве символа выступает не двоичный
символ (один бит), а элемент поля Галуа (несколько битов).
Порождающий
полином кода Рида – Соломона, исправляющего s ошибок, должен содержать 2s
корней:
{aj0, aj0+1, aj0+2,…, aj0+2s-1},
где j0 –
конструктивный параметр.
Как
правило, j0 выбирают равным 1. Тогда множество корней полинома
принимает вид {a, a2, a3… a2s}.
Для кода
Рида – Соломона, исправляющего s ошибок, порождающий полином имеет следующий
вид:
RS(х) = (х - a)(х - a2)(х - a3)…(х - a2s),
При
таком представлении очевидно, что порождающий полином имеет множество корней {a, a2, a3… a2s}.
2. Коды Рида–Соломона, исправляющие
одиночную ошибку
Для кода
Рида–Соломона, исправляющего одиночную ошибку (s=1), порождающий полином имеет
вид RS(х) = (х - a)(х - a2).
Возможно
несколько форм записи порождающего полинома для кодов Рида–Соломона. Как правило,
для построения кодов Рида–Соломона используют расширения поля GF(2) над
примитивным полиномом p(z). В этом случае, в соответствии с определением
примитивного полинома, элемент поля z является примитивным. Поэтому вместо
обозначения примитивного элемента a можно использовать z:
RS(x) = x2 + (a + a2)*x + a3 = x2 +
(z + z2)*x + z3.
Другая
форма будет зависеть от того, какое именно поле используется для построения
кода Рида-Соломона. Поэтому эту форму рассмотрим на примере.
Пример.
Построим поле Галуа GF(8) как расширение поля GF(2) над примитивным
полиномом р(z) = z3 + z + 1. Элементы поля могут
быть представлены в различном обозначении.
|
В виде степени |
В виде полинома |
В двоичном виде |
|
0 |
0 |
000 |
|
a0 |
1 |
001 |
|
a1 |
z |
010 |
|
a2 |
z2 |
100 |
|
a3 |
z + 1 |
011 |
|
a4 |
z2 +z |
110 |
|
a5 |
z2 + z + 1 |
111 |
|
a6 |
z2 + 1 |
101 |
Поскольку
RS(x) = x2 + (z + z2)*x + z3, а (z + z2) для рассматриваемого поля
GF(8) в степенном обозначении a4, z3 - a3, то порождающий полином можно
представить в следующей форме: RS(x) = x2 + a4x + a3.
При
изменении j0 также изменяется порождающий полином.
Например, при j0=2 RS(x) = (x - a2)(x - a3) = x2 + (z3 + z2)x + z5. Для GF(8) над р(z) = z3 + z + 1 RS(x) = x2 + (z2 + z + 1)x + z2 + z + 1 = x2 + a5 x + a5.
Кроме
того, отметим, что элементы поля в общем виде для поля GF(8) можно обозначить: a2z2 + a1z + a0, где а2,
а1, а0 – коэффициенты, принимающие разные значения. Эти
элементы поля - в данном случае триады -
являются символами кода Рида – Соломона.
3. Кодирующие и декодирующие
устройства
Итак,
для кода Рида-Соломона, исправляющего одиночные ошибки, получены разные формы
порождающих полиномов:
1) RS(х) = (x - a)(x - a2) при j0 = 1;
2) RS(x) = (x - a2)(x - a3) при j0 = 2;
3) RS(x) = x2 + (z + z2)*x + z3 при j0 = 1;
4) RS(x) = x2 + (z3 + z2)x + z5 при j0 = 2;
5) RS(x) = x2 + (z + z2)*x + z + 1 при j0 = 1;
6) RS(x) = x2 + (z2 + z + 1)x + z2 + z + 1 при j0 = 2;
7) RS(x) = x2 + a4x + a3 при j0 = 1;
8) RS(x) = x2 + a5 x + a5 при j0 = 2.
Формы 1,
2 являются общими для разных полей Галуа, но для построения схем в таком виде
не используются. Все остальные формы могут быть использованы для построения
схем кодера и декодера, при этом формы 3, 4 не зависят от конкретного поля
Галуа, формы 5-6 зависят от конкретного поля Галуа.
Нечетные
и четные варианты полиномов определяют разные коды – у них будет разная схемная
реализация, но основные параметры – корректирующие возможности, длина кода n, количество информационных k и проверочных n-k=p символов - одинаковы.
Как
правило, для представления функциональных схем кодирующих и декодирующих
устройств используют 7, 8 варианты порождающих полиномов, вид схем наиболее
компактный, но построение таких полиномов предполагает применение поля Галуа.
Для разработки
принципиальных схем лучше использовать 3-6 варианты полиномов, поскольку они не
требуют построения поля Галуа, причем 5, 6 варианты более предпочтительны.
Рассмотрим
примеры.
Для поля
GF(8) и порождающего полинома RS(x)
= x2 + a4x + a3 код Рида-Соломона, исправляющего одну ошибку (одну триаду – три двоичных
символа) имеет следующие параметры: длина кода n=7, количество проверочных символов
p=degRS(x)=2, количество информационных
символов k=n-p=5. Таким образом, реализуем (7,
5)-код Рида-Соломона, причем числа 7 и 5 означают количество триад двоичных
символов.
Кодер
этого кода аналогичен кодеру циклического кода Хэмминга. Как и для кодов
Хэмминга, кодер систематического кода Рида-Соломона представляет собой схему
умножения на полином xP и деления на порождающий полином; кодер
несистематического кода Рида-Соломона представляет собой схему умножения на
порождающий полином. Отличие в этих кодах - разная интерпретация символа
кодового слова и, соответственно, элементов памяти и умножителей на константу.
Схема
декодера аналогична декодеру Меггитта для циклического кода Хэмминга, за
исключением того, что каждый элемент задержки в данном случае не один элемент
памяти, а три. Кроме того, у этой схемы специфические умножители на константу.
Именно эти умножители и представляют затруднение при преобразовании
функциональной в принципиальную схему. Особенности реализации для кодеров и
декодеров одинаковы, поэтому рассматривать их будем на примере декодеров.
Для
порождающего полинома RS(x) = x2 + a4x + a3 декодер имеет вид, представленный на рисунке
1.
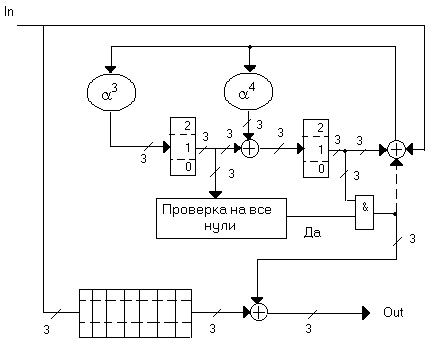
Рисунок 1 - Первый вариант декодера (7, 5)-кода
Рида-Соломона
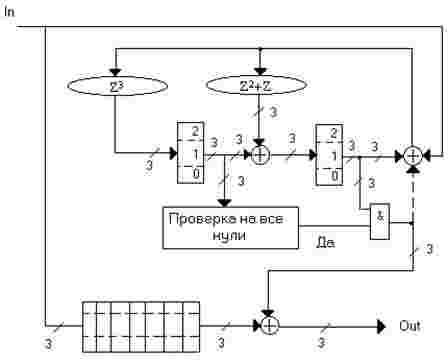
Для порождающего полинома RS(x) = x2 + (z + z2)*x + z3 декодер имеет такой же вид за
исключением умножителей на константы (рис. 2)
Рассмотрим пример реализации умножителя на константу z3..
Чтобы поставить ему в соответствие схему на двоичных элементах, определим (a2z2 + a1z + a0)*z3 mod
p(z).
Рисунок 2 - Второй вариант декодера (7, 5)-кода
Рида-Соломона
![]() a2z5 + a1z4
+ a0z3 z3
+ z +1
a2z5 + a1z4
+ a0z3 z3
+ z +1
![]() - a2z5 + a2z3
+ a2z2
- a2z5 + a2z3
+ a2z2
a1z4
+ (a2+a0)z3+a2z2 a2z2 + a1z
+ (a2+ a0)
- a1z4 + a1z2
+ a1z
(a2
+a0)z3 + (a1 +a2)z2 + a1z
-(a2 +a0)z3 + (a2
+a0)z + (a2 +a0)
(a1
+a2)z2 + (a0 + a1 +a2)z
+ (a2+ a0)
По полученному остатку от деления строится схема умножителя
на константу.
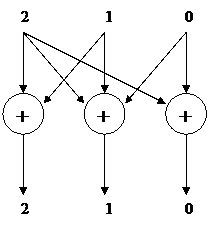
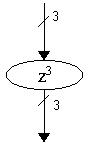
а) б)
Рисунок
3 – а – умножитель
на константу z3, б – умножитель на
константу z3 на основе сумматоров по модулю два
Получить остаток R от деления для реализации схемы
умножителя на константу (z2 + z) можно с помощью
нескольких операций умножения и деления на примитивный полином p(z):
1. (a2z2 + a1z + a0)*z2
= a2z4 + a1z3 + a0z2
![]() a2z4 + a1z3 + a0z2 z3 + z +1
a2z4 + a1z3 + a0z2 z3 + z +1
![]() - a2z4 + a2z2
+ a2z
- a2z4 + a2z2
+ a2z
a1z3
+ (a2+a0)z2+a2z a2z + a1
- a1z3
+ a1z + a1
(a2
+a0)z2 + (a1 +a2)z + a1 остаток R1
2. (a2z2
+ a1z + a0)*z = a2z3 + a1z2
+ a0z
![]() a2z3 + a1z2 + a0z
z3 + z +1
a2z3 + a1z2 + a0z
z3 + z +1
![]() - a2z3 + a2z
+ a2
- a2z3 + a2z
+ a2
a1z2
+ (a2+a0)z+a2 a2
остаток R2
3. R = R1 + R2
(a2 +a0)z2 + (a1 +a2)z
+ a1
+ a1z2
+ (a2+a0)z+a2________
(a2 + a1 + a0)z2 + (a1 + a0)z+(a2 + a1)
![]()
![]()
![]()
3
а)
![]()
![]()
3
а) б)
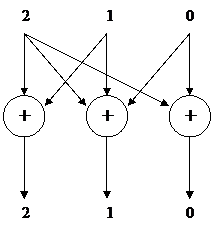
Рисунок
4 – а – умножитель
на константу z3 + z, б – умножитель на
константу z3 + z на основе сумматоров по модулю два
Таким
образом, получив представление умножителей на константу в виде схемы на трех
сумматорах по модулю два, преобразовать функциональные схемы кодирующих и
декодирующих устройств в принципиальные не составит особых затруднений.
4. Корректирующие возможности кодов
Рида-Соломона
Коды Рида-Соломона можно использовать для
исправления ошибок, как в параллельном, так и в последовательном потоке
двоичных символов.
Код Рида
– Соломона (7,5) позволяет исправить:
- одну ошибочную триаду в последовательности
триад длиной 7;
-
пакет ошибок длины 3 в последовательном коде двоичных символов с ограничением
на характер расположения пакета ошибок в последовательности символов длины 21.
Несколько
замечаний по поводу указанного ограничения на примере рассматриваемого кода.
При преобразовании триад в последовательный код на выходе кодера,
последовательность двоичных символов можно разделить на участки по три символа.
Если пакет ошибок попадает в один из таких участков, он будет исправлен. Если
же пакет ошибок захватывает два таких участка, то декодер не сможет его
исправить, поскольку, после преобразования последовательного кода в
параллельный, на входе декодера ошибки будут располагаться в двух триадах. Это соответствует двойной ошибке в символах
кода Рида-Соломона, поэтому декодер не сможет ее исправить.
В общем случае для кода поля Галуа GF(2b), эти ситуации можно изобразить
следующим образом:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() b b b b b b . .
. b
b b b b b b . .
. b
![]()
![]()
![]()
![]()
![]()
![]()
Неисправляемый Исправляемый
пакет
ошибок пакет ошибок
Рисунок
5 - Преобразование
триад (символов кода Рида-Соломона) в последовательный
код
Чтобы
снять ограничение на характер расположения ошибок и, кроме того, увеличить
корректирующие возможности, используют посимвольное перемежение кодов Рида –
Соломона, исправляющих одиночную ошибку.
Например,
при посимвольном перемежении кода Рида – Соломона (7,5) с параметром
перемежения j = 3 получаем код Рида-Соломона (21, 15), который позволяет
исправить:
-
для параллельного кода пакет 3 искаженные триады без ограничения на
характер расположения ошибок;
-
для параллельного кода 3 искаженные триады с ограничением на характер
расположения ошибок;
-
для последовательного кода пакет ошибок длины 7 (без ограничения на характер
расположения ошибок); пакет длины 9 или 3 пакета длины 3 или 1 пакет длины 6 и
1 пакет длины 3 (с ограничением на характер расположения ошибок).
В общем
случае длина исправляемого пакета ошибок для последовательного кода без
каких-либо ограничений равна b’ = j*b – (b - 1) для посимвольно
перемеженного кода Рида-Соломона поля Галуа GF(2b) с параметром перемежения j.
Схему
посимвольно перемеженного кода Рида-Соломона можно получить из схемы исходного
кода, вставив дополнительно к каждому элементу памяти j-1 элементов. Например, для поля GF(23) при перемежении с
параметром j=5 каждую
триаду элементов памяти нужно заменить пятью последовательно включенными
триадами. На рисунке 6 приведен вариант декодера для j=2. Отметим, что такой же способ
построения схемы посимвольного перемежения без необходимости построения
порождающего полинома можно применять и для двоичных циклических кодов над
полем GF(2).
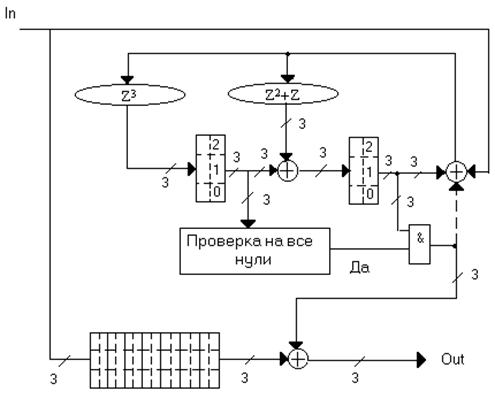
Рисунок 6 – Декодер для
посимвольно перемеженного (7,5) кода Рида-Соломона с параметром
перемежения j=2
Увеличить
корректирующие возможности кодов Рида-Соломона можно и другим способом. Для
этого необходимо изменить порождающее поле Галуа на большее количество
элементов, например, вместо поля GF(23) использовать GF(24).
Однако в этом случае для построения принципиальных схем кодера и декодера, надо
не только выполнить простую замену элементов памяти – вместо триад поставить тетрады,
но также необходимо снова преобразовать умножители на константы в схемы на
сумматорах по модулю два.
Выводы
Рассмотрена комплексная оценка
способов схемной реализации кодов Рида-Соломона – от построения порождающих
полиномов и выбора их оптимальной формы
для последующего синтеза устройств до функциональных схем кодеров и декодеров. На
примере кодов Рида-Соломона, исправляющих одиночную ошибку, показаны
особенности преобразования функциональных схем декодеров в принципиальные; предложен
способ повышения корректирующих возможностей кодов.
Полученные результаты могут
оказаться полезными при разработке устройств, исправляющих пакетные ошибки, или
для построения устройств компактного тестирования с возможностью локализации
пакетных ошибок. Кроме того, многие вопросы, связанные с построением кодов
Рида-Соломона, которое использует математический аппарат алгебры полей Галуа,
становятся более понятными при иллюстрации их конкретными примерами аппаратной
реализации.
Литература
1. Robert H. Morelos-Zaragoza. The Art of
Error Correcting Coding. First Edition, John Wiley & Sons, 2002. –
221p.
2. R.E.Blahut. Theory and Practice of Error
Control Codes. Addison-Wesley Publishing Company,
3. Питерсон У.,
Уэлдон Э. Коды, исправляющие ошибки. - М.: Мир, 1976. - 595с.