УДК 621.314

 

 Анализ выходного напряжения многоуровневого преобразователя частоты при регулировании в соответствии с пространственным вектором напряжения

 

Баранов А.В., студент; Шавёлкин А.А., доц., к.т.н.

(Донецкий национальный технический университет, г. Донецк, Украина)

 

Для многоуровневых преобразователей частоты (МПЧ) применяются различные методы регулирования выходного напряжения как с использованием ШИМ, так и без. В качестве базового при амплитудном регулировании следует рассматривать регулирование в соответствии с пространственным вектором напряжения. Эффективность того или иного способа регулирования предполагает оценку гармонического состава выходного напряжения, что и является целью данной работы.

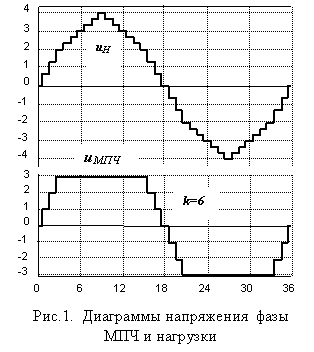
Рассмотрим особенности расчета гармонического состава и действующего значения фазного напряжения на нагрузке. Каждому уровню напряжения фазы МПЧ u_МПЧ соответствует 2 уровня пространственного вектора напряжения траектория которого - шестигранник. Обозначим номер шестигранника k=1,2,3. Одновременно с этим k соответствует количеству уровней напряжения u_МПЧ отличных от нуля (рис.1). При четных значениях k относительная продолжительность, которая соответствует данному уровню напряжения (значения i=1,2,3..) определяется как:

         .                                                       (1)

Амплитуда гармоник напряжения  с кратностью ν:

,                      (2)

   де: ν=6n±1 и n=1,2,3….

При нечетных значениях k относительная продолжительность для  последнего уровня , для остальных при  значения .

При этом амплитуда гармоник напряжения:

 

Период выходного напряжения на фазе нагрузки u_Н можно разделить на 6k интервалов . Количество уровней в полуволне выходного напряжения на фазе нагрузки р=2k, причем  один уровень составляет  (в относительных единицах 1/3). Принцип формирования напряжения на фазе нагрузки при четных  и нечетных k имеет свои закономерности. Это касается сдвоенных на интервале уровней, количество которых k₂. При  четных значениях k полуволна напряжения u_Н начинается со сдвоенных уровней (рис.1). При нечетных значениях k сдвоенные уровни отсчитываются, начиная со второго в полуволне уровня.

Для определения действующего значения достаточно учесть только четверть периода. При этом длительность последней ступени составляет половину интервала, количество целых интервалов, где напряжение отлично от нуля – j.

При нечетных k=1,3,5,…

, .

Относительное значение напряжения на iтом - интервале (ступени):

, если i≤k₂

, если i>k₂.

Действующее значение напряжения:

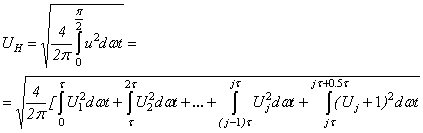
После преобразования получаем:

.

При  четных k=2,4,6,…

, .

Относительное значение напряжения на iтом - интервале (ступени):

, если i≤k₂

, если i>k₂.

Действующее значение напряжения определяется в соответствии с .

Коэффициент гармоник (THD):  .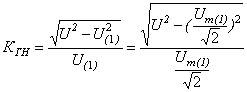

Значение коэффициента гармоник и относительное значение гармоник низкого порядка приведено в табл.1

Таблица1

Коэффициент гармоник выходного напряжения МПЧ