ВХОДНОЙ ТОК ДВАДЦАТИЧЕТЫРЕХФАЗНОЙ СХЕМЫ ВЫПРЯМЛЕНИЯ

С. И. Крючкова, рук. А. А. Шавелкин, к.т.н., доц.
Донецкий национальный технический университет

---

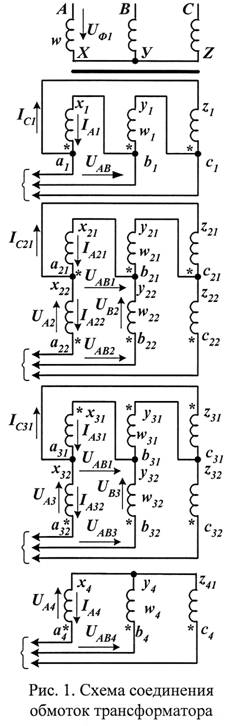
Актуальным вопросом при проектировании преобразовательных устройств является обеспечение электромагнитной совместимости с питающей сетью. Одним из способов является использование многофазных схем выпрямления [1]. Рассмотрим, как обеспечивается формирование входного тока в составной двадцатичетырехфазной схеме выпрямления. При этом четыре выпрямителя питаются от четырех комплектов вторичных обмоток, которые обеспечивают взаимный сдвиг|смещение| напряжений на угол 15˚.  Сдвиг|смещение|  фазы создается последовательным соединением обмоток разных|различных| фаз.

Рассмотрим вариант с использованием|употреблением| в качестве базовой схемы «треугольник|трехугольник|» (рис.1). Первый комплект обмоток соединен по схеме «треугольник|трехугольник|», при этом линейные напряжения равняются фазным. Четвертый комплект обмоток соединен по схеме «звезда|трехугольник|», при этом линейные напряжения (U_АВ4 на рис.2) опережают фазные на угол 30˚.  

Принимаем действующее значение напряжения за 1 (далее напряжения приводятся в относительных единицах). Линейное напряжение на зажимах второго комплекта U_АВ2 (между зажимами а₂₂ – в₂₂ на рис.1) определяется суммой линейного напряжения для схемы «треугольник» U_АВ1 (между зажимами а₂₁ – в₂₁) и напряжениями U_А2  и U_В2 на последовательно соединенных с «треугольником» катушках а₂₂, х₂₂ и в₂₂, у₂₂, соответственно. Напряжения U_АВ1 и U_А2  имеют ту же фазу, что и фазное напряжение U_А, их значения складываются  U_АВ1 +U_А2=к₁U_А (U_А2=к₂U_А). Напряжение U_В2 при добавлении (относительно к направлению обхода контура по 2-му закону Кирхгофа) имеет знак минус, то есть направлено противоположно фазному напряжению U_В (U_В2=к₂(-U_В)). Результирующее напряжение U_АВ2 (рис.2) опережает U_А на угол 15º и имеет те ж значения при условии, что коэффициенты к₁=cos45º/cos30º=0.816 и к₂=cos75º/cos30º=0.299. Разница их  (к₁-к₂)=0.517 и определяет напряжение обмотки по схеме «треугольник». Упомянутые коэффициенты определяются количеством витков в соответствующих обмотках.

Третий комплект обмоток отличается от второго встречным включением обмоток, соединенных в «треугольник|трехугольник|» (на рис.1 одноименные выводы обмоток отмечены) и соотношением напряжений на последовательно соединенных с «треугольником|трехугольником|» катушках а₃₂, х₃₂ и в₃₂, у₃₂:    U_А3=к₁U_А,     U_В3=к₁(-U_В).

Результирующее напряжение U_АВ3 (рис.2) опережает U_А на угол 45º. При этом результирующий ток фазы трансформатора содержит четыре составляющие от каждого из|с| комплектов обмоток. Для первого комплекта обмоток имеем ту же картину, что и для 12-ти фазной системы [1], ток i₁ при Ψ_k=0 (рассматриваем относительно|касательно| напряжения U_А) описывается выражением:

Для четвертого комплекта:

Для второго и третьего комплектов, исходим из|с| МДС| обмоток размещенных на общем стержне|стрежне| трансформатора (w₂₁, w₂₂ и  w₃₁, w₃₂).  Это дает возможность определить эквивалентный ток фазы, при этом следует учитывать, что ток в линейном проводе i₂₂  и i₃₂ (катушки w₂₂, w₃₂) равняется разнице|разности| фазных для схемы «треугольник»:

і_А=(√3і_А1 + і_А2+ і_А3+ і_А4)/n,

і_А2=0.517і_А21 + 0.299(і_А21 – і_С21)=0.816і_А21 - 0.299і_С21,

    і_А3=0.517(-і_А31) + 0.816(і_А31 – і_С31)=0.299і_А31 - 0.816і_С31,

 

где: n=w/w₄.

Линейные токи второго и третьего комплекта обмоток (токи на входе соответствующих выпрямителей) при одинаковой загрузке будут такие же, как и для первого комплекта. С учетом того, что результирующие линейные напряжения имеют сдвиг|смещение| по фазе, соответственно 15˚ и 45˚, такой же сдвиг|смещение| при одинаковых значениях будут иметь и токи в фазах, то есть:

і_А21= f*₃(ωt + 15˚),  і_С21= f*₃(ωt + 15˚+120˚),

і_А31= f*₃(ωt + 45˚), і_С31= f*₃(ωt + 45˚+120˚).

 

Таким образом, эквивалентный ток фазы трансформатора:

Кратность гармоник  k=6l±1. Для основной гармоники (k=1) третья и четвертая, пятая и шестая составляющие (1) при сложении|прибавлении,додавании| попарно дают значение coswt, это касается и второй (Ψ_k=-π/6). Таким образом, амплитуда тока увеличивается в четыре раза (соответствующая векторная диаграмма приведена на рис.3, где ось действительных чисел, которая соответствует фазе а расположена вертикально).

Для l =1 и нечетных|четных| значений l гармоники (5-я,7-я,17-я,.. гармоники) токи первого, четвертого и второго, третьего комплектов обмоток в противофазе и взаимно компенсируются (на рис.4 показана векторная диаграмма для k=5), сумма их равняется 0. Так, при k=5 фазы векторов, которые соответствуют третьей и четвертой составляющим составляют Ψ₂=5×15˚=75˚ и  Ψ₃=5×135˚=675˚=(2×360˚- 45˚), результирующий  вектор I_А2(5) имеет ту же амплитуду, что и вектор I_А1(5), но опережает по фазе на Ψ=90˚, для пятой и шестой составляющих имеем  Ψ₄=5×45˚=225˚ и Ψ₅=5×165˚=825˚=(2×360˚+105˚), результирующий вектор I_А3(5) имеет ту же амплитуду, что и вектор I_А1(5), но отстает по фазе на Ψ=90˚.

При четных|нечетных| значениях l (11-я,13-я гармоники) токи I_А1(11)=I_А4(11), а I_А2(11)=I_А2(115). Указанные пары токов имеют противоположные фазы и при равенстве амплитуд взаимно компенсируются.

Выражение (1) можно свести к виду

Таким образом, 24х - фазная схема выпрямления обеспечивает полное подавление высших гармоник тока, потребляемого из сети переменного тока при симметрии нагрузки всех четырех выпрямителей для всех l за исключением значений кратных 4.

24-х фазную схему выпрямления можно рассматривать как две 12-ти фазные при этом для нечетных|четных| значений l (5-я,7-я,17-я,.. гармоники) подавление достигается независимо от нагрузки. При четных|нечетных| значениях l (11-я,13-я гармоники) и несимметрии нагрузки подавление гармоник частичное – результирующее значение гармоники тока определяется разностью соответствующих гармоник.

Литература

1. Перетворювальна техніка. Навчальний посібник/ О.О. Шавьолкін,
   О.М. Наливайко. – Краматорськ, ДДМА, 2008.- 326с.