Применение универсальной математической модели формоизменения свободного контура для определения формы и площади контакта в вытяжных калибрах

Солод В.С.
Бенецкий А.Г.
Кулагин Р.Ю.

Источник: Металл и литье Украины.- 2006. - №7-8. - с.49-51

Известно [1], что при расчете энергосиловых параметров прокатки в вытяжных калибрах с применением метода приведенной или соответственной полосы ошибки в некоторых случаях могут достигать 45 - 60%. Большая часть ошибок при этом обусловлена неточным определением проекции поверхности контакта металла с валком. Для повышения точности расчета в работе [1] предложены эмпирические зависимости, которые, по мнению самих авторов применимы лишь для тех условий, в которых они получены.

В работе Г.Цоухара [2] также предложены инженерные формулы для расчета площади проекции поверхности контакта полосы с валком (площади контакта), основанные на приближенном описании формы очага деформации прямоугольниками и трапециями, однако их применение также ограничено рамками исследованных систем.

Для повышения точности определения формы и площади контакта полосы с валком нами предложена универсальная математическая модель формоизменения металла в вытяжных калибрах. В основу математической модели положены два локальных правила преобразования контура, а именно правило поперечного «прилипания» и правило распределения уширения по высоте, ее существо подробно описано в работе [3]. Указанная математическая модель позволяет пошагово строить контуры очага деформации с учетом закономерности развития уширения металла на свободном от контакта контуре, на основе сформулированных правил, а также зависимости задающей уравнение контура уширения в виде


где bо и b - начальная и конечная ширина полосы соответственно; Ld - длина очага деформации.

Для подтверждения возможности использования предлагаемой математической модели при описании формы и расчете площади горизонтальной проекции линии контакта полосы с валком использовали экспериментальные данные, полученные Г. Цоухаром, [2] для систем калибров «овал-квадрат», «овал-круг», «ромб-квадрат», «ромб-ромб».

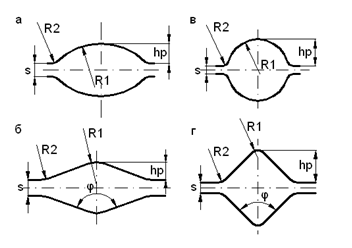
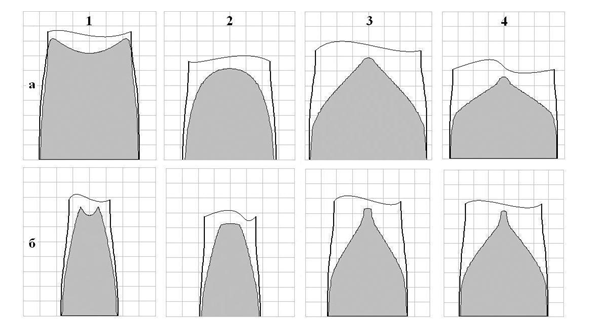
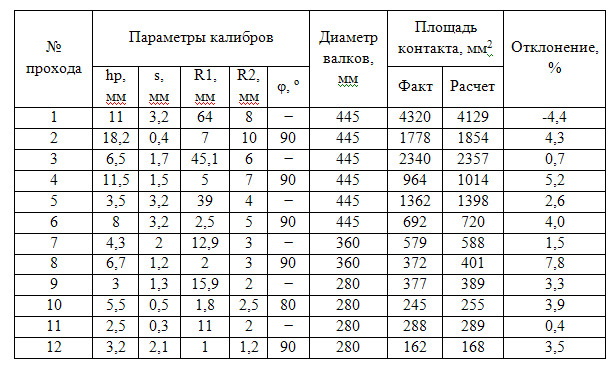
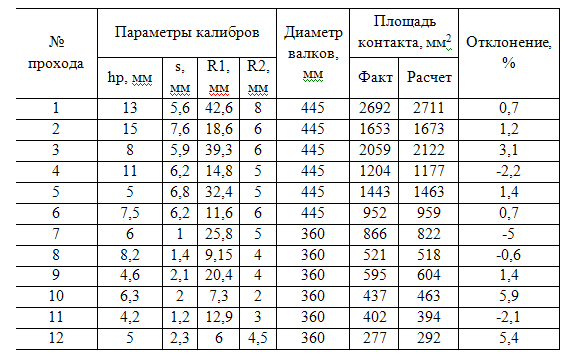
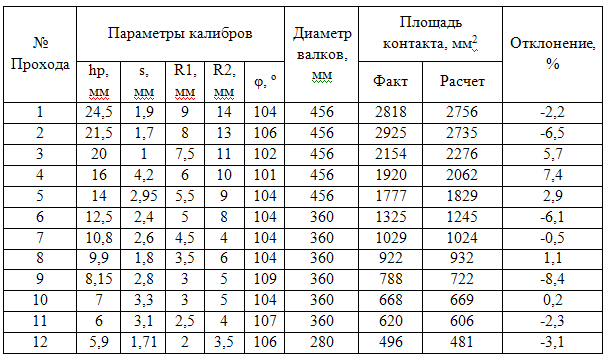
В результате моделирования формоизменения метала в калибрах, форма и условные обозначения парамеров которых показаны на рис.1, а размеры - в табл. 1-4, установлено, что уравнение контура уширения показанное выше нуждается в корректировке вследствие разных условий развития уширения по длине очага деформации, для калибров, с разной формой ручьев. Учитывая это, уравнение контура уширения на горизонтальной оси симметрии сечения предложено использовать в виде


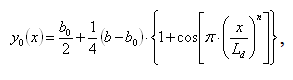
где n - показатель степени, характеризующий форму калибра (n=1...2), зависящий от среднеинтегральной характеристики tgqср угла наклона стенки калибра к горизонтали qср на участке контакта калибра с полосой


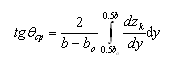
Показатель n определяется по формуле n = 2-tgqср при tgqср<1 , а при tgqср≥1 принимаетсяравным 1.

Следует отметить, что такая корректировка практически не влияет на форму и площадь поперечного сечения раската на выходе из валков. На рис.2 приведены рассчитанные по предлагаемой модели поперечные сечения раскатов с учетом коэффициента формы калибра n.

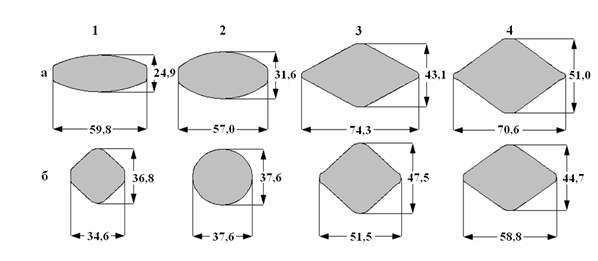
Рисунок 1 - Обозначения параметров калибров (а - овального, б - ромбического, в - круглого, г - квадратного), (hp - глубина вреза ручья, s - зазор, R1 и R2 -радиусы у дна ручья и бурта валка, φ - конструктивный угол ручья)

Результаты применения модели в виде расчетных формы и размеров контактных поверхностей с учетом коэффициента формы калибра n приведены на рис.3 и в табл. 1-4. Затененная область на рисунке отображает площадь контакта полосы с валком, жирной линией показан контур максимальной ширины (уширения) раската.

Формы поверхности контакта и поперечных сечений раскатов полученные по предложенной модели визуально хорошо соответствуют экспериментальным (см. [2]).

Рисунок 2 - Поперечные сечения раскатов (в первых - (а) и во вторых - (б) проходах вытяжных систем: 1-«овал-квадрат»; 2-«овал-круг»; 3-«ромб-квадрат»; 4-«ромб-ромб»).

Рисунок 3 - Горизонтальные проекции линии контакта полосы с валком (в первых - (а) и во вторых - (б) проходах вытяжных систем: 1-«овал-квадрат»; 2-«овал-круг»; 3-«ромб-квадрат»; 4-«ромб-ромб»).

Таблица 1 - Размеры калибров и результаты сравнения экспериментальных и расчетных площадей контакта по проходам для системы калибров «овал-квадрат»

Таблица 2 - Размеры калибров и результаты сравнения экспериментальных и расчетных площадей контакта по проходам для системы калибров «овал-круг»

Таблица 3 - Размеры калибров и результаты сравнения экспериментальных и расчетных площадей контакта по проходам для системы калибров «ромб-квадрат»

Таблица 4 - Размеры калибров и результаты сравнения экспериментальных и расчетных площадей контакта по проходам для системы калибров «ромб-ромб»

Выводы

Погрешность расчета площадей для описанных систем выраженная среднеквадратичным отклонением составляет: для поперечных сечений по всем системам 1,3%, для площади контакта в системах «овал-квадрат» - 4,0%, «овал-круг» - 3,1%, «ромб-квадрат» - 3,9%, «ромб-ромб» 4,7%.

Полученные результаты позволяют сделать заключение о возможности использования разработанного принципа описания свободного контура раската при разработке компьютерных алгоритмов моделирования сортовой прокатки в вытяжных калибрах.

Литература

1. Смирнов В.К., Шилов В.А., Инатович Ю.В. Калибровка прокатных валков. - М.: Металлургия, 1987.-368с.

2. Цоухар Г. Силовые воздействия при прокатке в вытяжных калибрах, пер. с нем. В.Г. Дрозда, под ред. Е.С. Рокотяна. - М.: Металлургия, 1963.-103с.

3. Солод В.С., Кулагин Р.Ю., Бейгельзимер Я.Е. Универсальная математическая модель формоизменения металла в вытяжных калибрах// Сталь.- 2006.- № 8.- с.16-18.