Abstract
We discuss design considerations for radiometers that use correlation to difference powers between two positions on the sky. Our summary of theoretical analysis and practical experience with the GBT’s Ka-band correlation radiometer is that symmetry is a key design principle, as is usual good practice for high-performance radiometer design.
1. Introduction
This memorandum summarizes design considerations for radiometers that use correlation to difference powers between two positions on the sky. Radiometers with this architecture have many names: continuous comparison [1, 2], differential [3], or correlation radiometers [4], and correlation [5] and pseudo-correlation [6] receivers. We discuss general correlation radiometer design considerations, whatever the names, based on a combination of theoretical considerations and our experience with the Green Bank Telescope’s (GBT’s) Ka-band correlation radiometer. An ideal correlation radiometer produces the power difference between two neighboring positions on the sky; it is a high-frequency differential amplifier for powers. This mode contrasts with usual total-power radiometry, in which the output is a difference of sequential observations of the two sky positions. The principal advantage to the continuous comparison arrangement is higher stability than total-power radiometers: receiver gain fluctuations multiply the small difference signal rather than the much larger system temperatures within the total power radiometer’s beam, so output fluctuations due to rapid gain fluctuations are proportionally smaller. The goal is to improve the radiometer system stability to a timescale long enough that moving the telescope to interchange the two beams on the source (a telescope “nod”) on a timescale of tens of seconds removes drifts and fluctuations, eliminating the need for a fast “chop” with a timescale near or below a second.
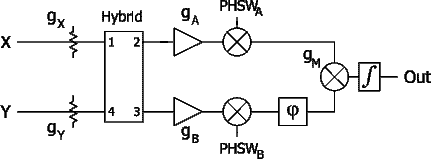
Figure 1: Correlation radiometer block diagram.
Figure 1 is a block diagram of a correlation radiometer. Signals from two feeds at positions X and Y in a focal plane combine in a hybrid, then pass on to amplification at the hybrid’s outputs. In this way signals from both sky positions simultaneously pass through the same amplifiers. Phase modulators follow to provide ±180◦ phase switching of the signal voltage, and an overall phase shift
provides proper phasing for correlation. A multiplier and integrator (a correlator) produce the cross-correlation function (the second hybrid in the GBT’s Ka-band radiometer is part of a multiplier circuit; see sec. 2.4). Standard circuits for the multiplier include a 180° hybrid and pair of power detectors (the GBT’s CCB), a 180° hybrid and pair of autocorrelation spectrometers (the GBT’s Spectrometer), or direct voltage multiplication in transistor multipliers (the Zpectrometer). All of these circuits are identical in function, differing only in implementation (sec. 2.4).
In the ideal case, the cross-correlator’s output u is
 |
(1) |
where TX,Y are the input radiation temperatures and Ê is a constant that accounts for system gain and unit conversions. A more complete expression for the output of the cross-correlator is
 |
(2) |
where Gx= |gx|2 and GY are the power gains (generally less than unity) of the elements before the hybrid, TOX and TOY are offsets in the inputs, α and β are the voltage transmission coefficients of the hybrid, ga,b are the complex voltage gains after the hybrid, Φ is the differential phase between the two circuits between the hybrid and the multiplier, gm is the complex multiplier responsivity, and u0 is a correlator output offset. Recasting equation (2) into a somewhat more convenient form,
 |
(3) |
In the following we discuss the terms in equation (3) and explore ways to reach the ideal case described by equation (1).
2. Design principles
2.1. Symmetry before the hybrid
The term in equation (3)’s square brackets shows why receivers with gain before the hybrid are impractical: for good common-mode rejection and low offsets the gains must be extremely well matched, frequency by frequency, across the entire band. Excellent matches for the input losses as a function of frequency of the components before the hybrid are also needed for good common-mode rejection and low offset ∆T0. Tight matching is more practical with simple passive components. Poor common mode rejection implies poor sky noise rejection: an offset provides a signal for gain instability to affect, so stability suffers. We had direct experience with gain imbalance with the Ka-band radiometer, where we traced the large output offsets and consequent stability degradation to reflection loss mismatches involving the orthomode transducers (OMTs) [7, 8, 9]. Symmetry is the key to reducing the mismatch imbalances in gain and phase, especially across broad bands, and the radiometer performance improved substantially when we removed the OMTs [10] and reconfigured the circuit to be as symmetrical as possible.
Reflections from circuitry before the hybrid (S22 for the components before the hybrid) produces offsets from noise radiated by components following the hybrids. The offset will have an amplitude proportional to the power reflection coefficient difference. Reducing the contribution of reflected and then correlated noise is the reason that some correlation radiometers have isolators between the hybrid and subsequent amplifiers. Ensuring a good match to the feeds is important to reduce spurious correlation offsets.
Noise radiated from the amplifier inputs will pass through the hybrid and radiate from the feed antennas. Coupling from one feed to another provides another path to produce a correlated signal. Cross-polarizing the input feeds attenuates the coupled signals [3], but at the cost of introducing some asymmetry. The Ka-band receiver without the OMTs is linearly cross-polarized with two 45° waveguide twists, which are identical except for the sense of twist. This maximizes symmetry to minimize the differential reflections, while still providing cross-polarized beams.
An analysis that includes noise terms [11] shows that cross-polarizing the inputs of radiometers with 180° input hybrids also rejects a term from correlated field emission from the atmosphere that is common to both beams. It is unclear how well these cross-polarization arguments hold within the very near fields of the horns and antenna, but there should be a useful effect. The GBT Ka-band radiometer is patterned on the WMAP architecture, which has a 180° hybrid. Rejecting atmospheric effects is obviously not a concern for space-based radiometers (e.g. WMAP); symmetry in the input circuit is more important for ground-based radiometers.
2.2. The hybrid
Superior phase smoothness and amplitude balance over broad bands, as well as improved rejection of post-hybrid and some atmospheric noise terms, favor 90° branch-line hybrids over 180° “magic tee” or ring hybrids. If the first hybrid is a 90° device, a second 90° phase shift, probably produced by another hybrid, is needed before correlation. Reference [11] contains a comparative analysis of the two hybrid types and provides references for hybrid properties and performance.
Balancing the hybrid’s voltage transmission coefficients, α and β, gives the maximum signal. Hybrid balance is only important for signal loss; imbalance does not generate spurious correlations by itself. Leakage between nominally isolated hybrid ports causes signal loss and allows signals to couple from one port to another, but this is not a major source of offsets since the signals generally have little correlation (e.g. amplifier noise with input signal). A hybrid phase deviation δθ from ideal decreases the output signal by a factor cos(δθ). Phase shifts later in the system can correct for the hybrid’s phase deviations, but the correction must be appropriate at every frequency across the band, a general problem that we discuss in sec. 2.3.
2.3. Symmetry after the hybrid
Symmetry in the circuits at the hybrid’s outputs preserves phase balance, which is necessary both to retain the signal and to minimize nonideal terms that are not apparent in this simple analysis (reference [11] covers noise and imbalance; reference [4] covers amplifiers that are dissimilar in phase, amplitude, and bandwidth). Amplitude balance is less important than phase balance because amplitude imbalances do not introduce nonideal terms, but simply change the signal’s strength. In principle it is possible to compensate for phase errors stemming from phase mismatches in the complex voltage gain product gagb* and the hybrid’s phase deviation δθ by trimming a phase offset φ (Fig. 1). It is, however, practical to match only simple and smooth phase variations. This sets a requirement of well-behaved and well-matched phases throughout the entire receiver, something that is most easily accomplished by symmetry in the circuit layout.
2.4. Correlator
The correlator’s output is proportional to its two input voltages,
 |
(4) |
where the angle brackets indicate a time average from low-pass filtering or integration. Time averaging is the result of finite post-detection amplifier bandwidth or a separate integration circuit.
There are many ways to implement the correlator’s four-quadrant multiplication. The Ka-band setup uses two multipliers: the classical hybrid-and-two-power-detectors multiplier for the CCB and Spectrometer, and a Gilbert-cell transistor voltage multiplier for the Zpectrometer. In the former case the multiplier’s hybrid is mounted within the receiver structure with the power detection outside; in the latter case signals from the two amplifier chains feed the external Zpectrometer system.
Some radiometer descriptions drop the distinction between the multiplier section and the rest of the radiometer. We cover this approach in the Appendix, where we analyze the receiver as a beamswitching, instead of correlation, radiometer. Incorporating the multiplier circuit in the receiver obscures the basic receiver architecture and makes the overall system seem more complex. It also masks the close relationship with other correlation receivers, such as interferometers, that is apparent in Figure 1. The imperfections in the multiplier section itself then become less obvious. This muddling of multiplier and receiver properties led to the designation of “pseudo-correlation radiometer.” One might as well name a total-power radiometer with a power detector that deviates slightly from a perfect square law as a “pseudo-total-power radiometer.”
The principle behind the classical power detector multiplier circuit is straightforward. First, take the squares of a 180° hybrid’s voltage outputs,
 |
(5) |
Second, difference the power detector outputs to get
a value proportional to the voltage product of the hybrid’s input signals. Hybrid imbalances leave residual total power terms
va2 and vb2, which phase switching (sec. 2.6) reduces. Compensating for power detector responsivity, as discussed further in the Appendix, is necessary for many applications. References [2, 4, 12] describe some of the correction methods.
The Zpectrometer’s multiplier is a Gilbert-cell multiplier circuit [13] implemented with microwave transistors. Modulating transistor gain forms the basis of multiplication, for an output of
 |
(6) |
for va,b << vT, where vT = kT/q ≈ w 25 mV at room temperature. Although Gilbert cells are not perfectly linear, they are nearly so when the input voltages are small compared with vT. The Zpectrometer operates in the small-signal regime, and the multipliers are sufficiently linear for practical work.
2.5. Gain stability
The basic principle of differential radiometry is that the radiometer reduces the fluctuations by reducing the signal available for multiplication by system gain rather than by some form of gain stabilization. Intrinsic amplifier stability is still extremely important. The correlation architecture minimizes but cannot completely eliminate the effects of amplifier gain fluctuations, although phase switching may help; see sec. 2.6. Equation (3) shows that amplifier gains, the multiplier gain, and phase changes scale the inevitable residual offsets as gagb*gM cos(Φ).
Even if the radiometer is in perfect balance, with TX = TY on average, the difference fluctuates about zero, and gain fluctuations increase the output noise. Faris [4] calculated the noise produced by gain fluctuations for this case. He starts with amplifier gains related by a factor a,
| gb=[1+a(t)]ga | (7) |
If a(t) = a, a constant, the correlator’s output output scales by a2, another constant. If a(t) is a zero-mean stochastic function, the output noise increases by a factor (1 +a2)1/2 . A similar scaling applies to the multiplier gain or fluctuating phase.
Our measurements of the Ka-band system with cryogenic terminations at the hybrid inputs [9] showed Allan variance minimum times often beyond 100 seconds. At other times we recorded fluctuations correlated across many lags, indicating overall system gain fluctuations. We ruled out electric field pickup on the first-stage low noise amplifier (LNA) bias lines by driving 1 V p-p into a wire draped along the wiring harness and synchronously detecting the IF total power; we could not detect a signal. This result pointed to fluctuations in bias or ground potential (see sec. 2.6), rather than in pickup as the main cause of gain fluctuations.
Another potential source of gain fluctuations is changes in the standing wave pattern inside the cryostat [14]. The cryostat is a resonator whose dimensions can change with temperature and gravitational loading. Absorber within the innermost radiation shield of the GBT’s Ka-band receiver damps standing wave patterns that can couple into signal path optically or through cracks in component bodies or waveguide flanges.
2.6. Correlator offsets and phase modulation
Phase modulation is not a fundamental part of the correlation radiometer architecture; its purpose is to allow LNA operation above their 1/f gain fluctuation knees and to reduce offsets at the correlator output. Modulating at frequencies above 10 kHz pushes the detection above typical LNA gain fluctuation frequencies, improving stability (sec. 2.5). We varied the modulation frequency to map the improvement from 4.17, 6.25, and 10.4 kHz [7], verifying that rapid modulation decreases the radiometer noise. Since the multiplier 1/f knees are below a few kilohertz, we presumably traced the LNA noise spectrum. Efficiency considerations from the finite transition times for the modulators limit the upper phase switch frequency.
Phase modulation also removes offsets at the correlator outputs. Offsets may come from the correlator itself or, as we have seen with the Ka-band receiver, from electrical pickup synchronous with the receiver’s phase switching. It is likely that a slight ground loop through the receiver’s mechanical frame, which also serves as the ground return for both the phase switch and LNAs, is the cause of the pickup. Whatever the origin of the modulation, it must be stable to avoid compromising the overall system stability. Correlator offsets, the u0 term in equation (3), enter the analysis on a slightly different footing because they do not depend on the high-frequency gains.
We traced large offsets to small ground-loop currents in the Ka-band receiver frame from the phase modulator drive signals [7]. The modulators themselves are standard double-balanced mixers that are not electrically isolated from the rest of the receiver, and the current return included the receiver’s mechanical structure. Switching two modulators in quadrature, as shown
in the upper two traces in Figure 2, reduced the pickup to a satisfactory degree. Figures 8 and 9 in reference [9] show the effect particularly clearly. With quadrature switching, the only currents at the demodulation frequency (bottom trace in Fig. 2) come from small differences in the switch rise and fall times and, to a very small extent, waveform asymmetries from delays in the signal generation logic. We did not find pickup coupling through the receiver’s common power supply, a frequent conduit for synchronous pickup, so an isolated power supply for the phase modulator drives was unnecessary for the Ka-band receiver.
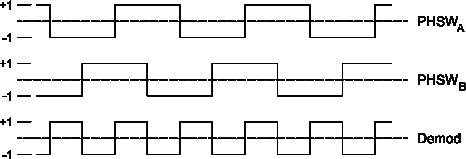
Figure 2: Quadrature modulation and demodulation waveforms.
The phase switching patterns in Figure 2 are low-order Walsh functions [15, ch. 7.5]. We experimented briefly with higher-order Walsh function switching sequences. These take higher-order derivatives of the input stream and should remove drifts and curvature as well as the constant term that the lowest-order Walsh functions eliminate. We did not find any improvements with the higher-order waveforms, perhaps because the drifts were small, and returned to the low-order waveforms for highest switching efficiency.
Unequal gain in the phase modulator’s states will produce an offset at the correlator output. A pure continuum radiometer can use different drive currents in the two states to produce gains that are identical on average [6], but this is not possible for a radiometer with multiple spectral channels unless the switch gains are absolutely flat across frequency. Quadrature switching with two modulators is an advantage here. If a single modulator has a gain difference of ∆g between the two states, the offset from quadrature switching will be ∆g2, which can be substantially smaller for reasonably well-matched modulator gain states. We have had experience with instruments that work well with a single active phase switch (as did WMAP [6]), but dual phase modulators preserve symmetry and generally perform better.
3. Total power measurements
Total power measurements are needed for calibration (e.g. atmospheric transmission, system temperature) and system characterization (e.g. receiver temperature). Since correlation radiometers are intrinsically differential, some supplemental total power monitoring is necessary. It may be possible to extract total power signals at the multiplier, depending on type (see the Appendix).
It is also possible to monitor the power before the multiplier inputs both for calibration and for setting the multiplier power levels. The multiplier input powers A and  (Fig. 1) are weighted sums of the input powers Px and Py:
 |
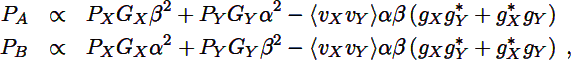(8) |
where the terms in angle brackets account for correlated power between the two beams. This term will be zero for independent blackbody loads covering each feed, and should be small if the signal arises in the telescope’s near field where the beam overlap is large but the feeds are cross polarized.
4. Conclusions
Design considerations for correlation radiometers include:
From this list we find two main summary points. First, symmetry is an overarching consideration for the highest common-mode rejection. Second, symmetry does not relieve the need for a well-engineered receiver: it should be built with all the care customary for high performance radiometry.
Acknowledgments
We thank D. Emerson for discussions of higher-order phase switching schemes. University of Maryland participation in this work was supported by the National Science Foundation’s ATI program and an NRAO Visitor’s Program award to AH.
References
[1] E.-J. Blum, “Sensiblite des radiotelescopes et recepteurs a correlation,” Ann. Astrophys., vol. 22, pp. 140-163, 1959.
[2] C. Predmore, N. Erickson, G. Huguenin, and P. Goldsmith, “A continuous comparison radiometer at 97 GHz,” IEEE Trans. Microwave Theory Tech., vol. MTT-33, pp. 44-51, 1985.
[3] S. Padin, “GBT 26-40 GHz radiometer: design considerations for the continuum section.” Report, California Institute of Technology, 2001.
[4] J. Faris, “Sensitivity of a correlation radiometer,” J. Res. Nat. Bur. Stand.-C, vol. 71C, pp.153-170, 1967.
[5] M. Tiuri, “Radio astronomy receivers,” IEEE Trans. Antenn. Propag., vol. AP-12, pp. 930-938, 1964.
[6] N. Jarosik, C. L. Bennett, M. Halpern, and 12 others, “Design, implementation, and testing of the Microwave Anisotropy Probe radiometers,” Astrophys. J. (Suppl), vol. 145, pp. 413-436, 2003.
[7] A. Harris, S. Zonak, K. Rauch, A. Baker, G. Watts, K. O’Neil, R. Crea-ger, B. Garwood, and P. Marganian, “Zpectrometer commissioning report, Fall 2006.” NRAO Green Bank Telescope memo series No. 245, 2007. http://wiki.gb.nrao.edu/bin/view/Knowledge/GBTMemos.
[8] A. Harris, S. Zonak, and G. Watts, “Symmetry in the Ka-band correlation receiver’s input circuit and spectral baseline structure.” NRAO Green Bank Telescope memo series No. 248, 2007. http://wiki.gb.nrao.edu/bin/view/Knowledge/GBTMemos.
[9] A. Harris, S. Zonak, and G. Watts, “Basic stability of the Ka-band correlation receiver.” NRAO Green Bank Telescope memo series No. 249, 2007. http://wiki.gb.nrao.edu/bin/view/Knowledge/GBTMemos.
[10] A. Harris, S. Zonak, and G. Watts, “Brief summary of results from modified Ka-band receiver tests.” Report, 2007. http://www.astro.umd.edu/ harris/kaband/aug07_report.txt.
[11] A. Harris, “Spectroscopy with multichannel correlation radiometers,” Rev. Sci. Inst, vol. 76, pp. 4503-+, May 2005.
[12] A. Mennella, M. Bersanelli, M. Seiffert, D. Kettle, N. Roddis, A. Wilkinson, and P. Mein-hold, “Offset balancing in pseudo-correlation radiometers for CMB measurements,” Astr. Astrophys., vol. 410, pp. 1089-1100, Nov. 2003.
[13] B. Gilbert, “A precise four-quadrant multiplier with subnanosecond response,” IEEE J. Solid-State Circuits, vol. 3, pp. 365-373, 1968.
[14] R. Norrod, “Cryostat cavity noise and the impact on spectral baselines.” NRAO Electronics Division Internal Report No. 318, 2007.
[15] A. R. Thompson, J. M. Moran, and G. W. Swenson, Jr., Interferometry and Synthesis in Radio Astronomy. New York: Wiley, second ed., 1991.
Appendix: Beamswitching mode
It is possible to use the separate outputs of the classical power detector multiplier to detect power in the individual beams and make an electronic beamswitching receiver. This may be useful if gains throughout the system and the detector responsivities are not well known or are not carefully matched. The following simplified analysis eliminates the distinction between the receiver and multiplier sections to explore the total power mode. Neglecting various constant terms, the output of the two detectors at the Σ and ∆ ports of the second hybrid are
 |
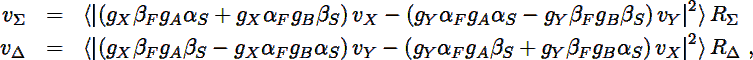(A.1) |
taking voltage transmission coefficients aF,S and βF,S for the first and second hybrids, gains including the modulator phase gA,B and detector responsivities of RΣ,∆ for the detectors following the second hybrid. For the ideal case, αF = αS = βF = βS = 1/√2 and gx = gr = 1, so equation (A.1) becomes
 |
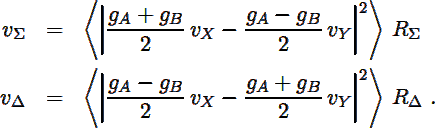(A.2) |
For ga = +1 and gb= -1, as an example, the detector outputs are
 |
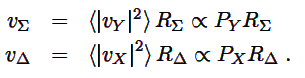(A.3) |
Here the Σ detector’s output is proportional to the power at the receiver’s X input, Px, and the ∆ detector’s output is proportional to the power at the Y input. Table 1 shows how the detector outputs correspond to different beams as the the modulator states change.
Table 1: Outputs of the power detectors at the second hybrid’s Σ and ∆ ports for different phase modulator combinations, from equations (A.2).
If RΣ = R∆, the ideal case, the difference of the detector voltages is the power difference at the receiver inputs: this is the correlation receiver with the the second hybrid and detectors used as a multiplier.
If RΣ ≠ R∆, the power difference is unequally weighted by responsivity. In this case, differencing each detector output separately will produce better common-mode rejection because the responsivity is the same for both input signal selections. This mode corresponds to a sequential beamswitching receiver, not a correlation receiver, with beam selection driven by the phase modulator settings. The tidy results in equations (A.2) and Table 1 deteriorate rapidly as the mixture of signals from both feeds apparent in equations (A.1) grows with imperfect phase modulator matches in both phase states and at all frequencies, with unequal hybrid voltage transmission coefficients across frequency, and with input gain imbalance.