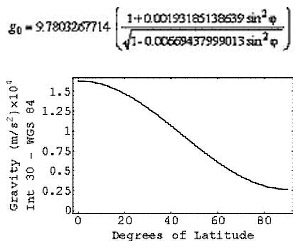
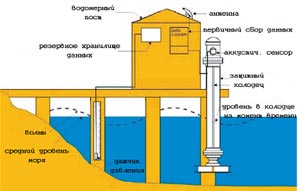
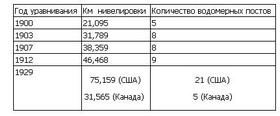
Введение: это первая часть работы, состоящей из четырех частей, посвященной фундаментальному понятию «что такое высоты». Национальная Геодезическая Служба (NGS) начинает программу по обновлению высотной основы, благодаря которой, в будущем, отпадет необходимость определять ортометрические высоты старых и новых нивелирных реперов. NGS присвоит реперам геодезические и ортометрические (по Гельмерту) высоты. Таким образом, производители работ столкнутся с необходимостью смены системы высот, в которой они работают. Хотя понятие «высота» - часто употребляется – найти его точное определение бывает затруднительно. В четырех работах мы поговорим о различных пониманиях высоты, использующихся в геодезии, и точном определении этого понятия в разрезе физических свойств потенциала силы тяжести; также разговор пойдет об определении высот из высокоточных GPS определений. Целью данной статьи мы ставили освещение существующих систем высот и самого понятия «высоты» с тем, чтобы избежать возможных ошибок со стороны геодезистов, тогда, когда будет введена новая система высот. Первая часть посвящена референц-эллипсоидам и поверхности относимости, связанной с уровнем моря. Вторая часть рассказывает о физическом аспекте высот, упрощенно описывает геоид и объясняет, почему уровень водомерных постов имеет разную ортометрическую высоту. Третья часть знакомит нас с геопотенциальными числами и динамическими высотами, объясняет поправку, которую необходимо вводить, вследствие непараллельности уровенных поверхностей и освещает, как эти поправки используются в NAVD 88; четвертая часть повествует о самых удачных примерах измерения высот при помощи GPS. Вступление Национальная Геодезическая Служба (NGS) отвечает за создание и поддержание пространственной геодезической сети США. В порядке соответствия современным требованиям, NGS начала программу модернизации системы высот, которая при удачном исходе должна вылиться в единую национальную систему позиционирования, реализованную жесткой высокоточной плановой, высотной и гравиметрической сетью, созданной и поддерживаемой при помощи GPS, и контролируемой Национальной Геодезической службой. В конечном итоге NGS планирует реализацию Национальной пространственной системы координат. В прошлом NGS производила высокоточные работы по созданию планового и высотного обоснования, представленного в каталоге геодезическими широтами, долготами и ортометрическими высотами. NGS отвечает за создание геодезической основы и занимается развитием, и внедрением современных технологий, для более эффективного развития, и поддержания государственной геодезической сети, к примеру, Сеть постоянно действующих станций GPS (CORS). Служба, совместно с другими организациями, работает над адаптацией новых технологий применительно к каждому району и виду работ таким образом, чтобы технологии могли покрыть частный сектор геодезических работ под строгим контролем NGS. Вместо закладки новых пунктов, NGS создала сеть постоянно действующих станций (известную как CORS) в расчете на то, что эта сеть в будущем обеспечит потребности в геодезической основе. Хотя при помощи GPS неплохо получаются плановые координаты, непосредственно измерение ортометрических высот с ее помощью невозможно. Получить можно только эллипсоидальные (геодезические) высоты. В прикладных целях редко требуется знание высот относительно эллипсоида, так что NGS были созданы сложные высокоточные многогармонические математические модели гравиметрического поля (Милберта 1991, Милберта-Смита 1996, Смита – Милберта 1999, Смилта-Романа 2001), которые используются для перевычисления эллипсоидальных высот в ортометрические высоты по Гельмерту. В результате, геодезисты, картографы и инженеры работают с сочетанием геодезических и ортометрических высот. Разумеется, чтобы осветить все тонкости вычислений, используемые при переходе от одной системы к другой, необходимо коснуться всех аспектов высот - превышений, ортометрических, геодезических, динамических высот, геопотенциальных чисел. Согласно геодезическому справочнику (NGS 1986) высота определяется, как расстояние, измеряемое по нормали между точкой и поверхностью относимости, например, высота самолета над землей. Хотя это определение кажется интуитивно понятным, оно дает довольно расплывчатое представление о том, что же такое поверхность относимости. Системы высот можно разделить условно на два типа – относящиеся к полю силы тяжести и относящиеся к эллипсоиду. Те высоты, которые отнесены к полю силы тяжести можно назвать геопотенциальными числами, а высоты, отнесенные к эллипсоиду – эллипсоидальными высотами. Между этими двумя системами высот нет прямой связи. Они относятся к разным поверхностям, и, как будет описано позже, отсутствие глобальных высокоточных знаний о структуре гравитационного поля препятствует прямому строгому переходу из одной системы в другую. Это аналогично тому, что между геодезическими датами разных лет NAD 83 и NAD27 не существует строгой связи. Определение и связь превышений, ортометрических, динамических высот, геопотенциальных чисел и геодезических высот довольно часто недопонимается многими практикующими инженерами. Это, возможно, неудивительно, поскольку существует огромное количество профессиональных жаргонизмов, относящихся к высотам. Справочник геодезиста содержит 17 определений слова «превышение» и 23 определения «высоты», несмотря на то, что почти 9 из них является определениями превышения. Целью этой статьи является внесение ясности в понятие слова «высота». Статья Статья состоит из четырех частей, в которых рассказывается о вертикальных поверхностях относимости, физическом смысле измерения превышения, сравнении различных типов высот и современную технологии определения ортометрических высот при помощи GPS измерений. Рисунки и таблицы имеют сквозную нумерацию для всех четырех частей. Первая часть – вводная. Целью ее является обоснование концепции построения нового вида сетей, обзор эллипсоидов, средних уровней моря и отсчетных поверхностей, использующихся в США. Вторая часть посвящена гравитационному полю. В ней рассказывается о силах, действующих на Землю, потенциальном поле, объясняется, почему гравитационное поле еще не определяет уровенные поверхности, в то время как их определяет Геопотенциальное число. Известен факт незамыкания сильно вытянутого нивелирного хода. Правда, немногие знают, что это справедливо и для ортометрических высот. Во второй части идет обсуждения ондуляций (высот) геоида и их влияния на высоты. В третьей части обсуждаются проблемы, связанные с динамическими высотами и ведется поиск их решения. В четвертой части идет обсуждение возможности определения высот с помощью GPS. При том, что точный пересчет геодезических высот в ортометрические требует знания материала, содержащегося в данном обзоре. Как сказано ранее, NGS пытается привить геодезическому сообществу новые методы. Мы полагаем, что данный обзор будет интересен инженерам, и поможет лучше понять смысл и специфику ортометрических высот и процесс перевычисления между разными системами высот. Следующий раздел будет посвящен обзору эллипсоидов, их использованию в геодезии и картографии. После следует часть, посвященная понятию среднего уровня моря и ортометрических высот, далее ведется обсуждение национальных поверхностей относимости (счета высот) США. Первая часть текущего документа заканчивается заключением. Референц-эллипсоиды Референц-эллипсоид, его часто называют сфероидом – это упрощенная математическая модель формы Земли. Однако в случае невысоких требований к точности картографирования, в качестве приближения Земли может использоваться сфера, когда требования к точности выше и сферическая модель уже не может удовлетворить им, вводят модель эллипсоида вращения. Эллипсоид вращения (или просто эллипсоид) – это фигура, которая получена вращением эллипса вокруг одной из осей. В геодезии используются сжатые (у полюса) эллипсоиды, так как полярная ось Земли короче, чем экваториальная. Локальные референц-эллипсоиды Геодезические даты и картографические системы координат зависят от того, какая математическая модель Земли лежит в их основе – относительно которой выполняются тригонометрические преобразования по вычислению координат точек Земной поверхности – переход между геоцентрическими, геодезическими и географическими координатами. Вычисления геодезических и географических координат требует знания эллипсоида (например их описывали Бугаевский и Шнайдер 1995, Qihe et al. 2000; Snyder 1987). Точно также, преобразование между геодезическими и прямоугольными координатами по Гельмерту требует знания эллипсоида. Как сказано выше, измеренные величины для геодезической обработки должны редуцироваться на единую поверхность, и референц-эллипсоид является такой поверхностью. Таким образом, горизонтальные поверхности относимости выбираются в зависимости от подходящего реферец-эллипсоида. До недавнего времени, форма и размеры референц-эллипсоидов устанавливались, исходя из результатов наблюдений в сетях триангуляции (Gore 1889; Crandall 1914; Shalowitz 1938; Schwarz 1989; Dracup 1995; Keay 2000). Существует, по крайней мере, два способа перейти к эллипсоиду – метод дуг (Эйри 1830, Эверест 1830, Бесселя 1841, Кларка 1866) и метод площадей (Хейфорд 1909). При помощи рулеток, цепей, проволок или реек измерялась длина, по крайней мере, одного базиса, лежащего между вершинами треугольника, после координаты и длины линий передавались при помощи триангуляции. В ранних сетях триангуляции высоты использовались для редуцирования и получались, главным образом, из тригонометрического или барометрического нивелирования, хотя в NАD27 «линия высокоточного нивелирования, повторяющего звено триангуляции начиналась с залива Чиспик и заканчивалась в Сан-Франциско 1907» (Dracup 1995). Эллипсоиды, установленные по результатам обработки сетей триангуляции были оптимальны для данной территории. В результате, для каждого района по результатам измерений выводился и ориентировался собственный эллипсоид и в итоге число референц-эллипсоидов постоянно увеличилось (в документах NIMA WGS 84 Update Committee (1997) и Meyer (2002) приведены параметры множества эллипсоидов). При триангуляции было невозможно создание единого, всеобщего реферец-эллипсоида – так как фрагменты сети были разделены значительными водными препятствиями. Местные эллипсоиды не давали вертикальной поверхности относимости в привычном ее понимании и не использовались в таком качестве. Геодезические высоты определялись как расстояние от точки до поверхности эллипсоида, имеющее положительное направление при удалении от эллипсоида вверх. Несмотря на строгость математического определения, на практике определение геодезических высот было затруднено по нескольким причинам. До GPS, все высокоточные определения производились при помощи нивелирования, геодезические высоты определялись по известным ортометрическим высотам и известному значению аномалий высоты, которые получали из астрономических и гравиметрических измерений. (Heiskanen and Moritz 1967, стр. 82-84). Вдобавок, положение центра местного эллипсоида относительно центра масс было произвольным, т.е. центр Земли не совпадал с центром масс, так что местные эллипсоиды не отражали никоим образом средний уровень моря. Например, центр эллипсоида Кларка 1866, использующегося в NAD27 на 236 метров удален от центра глобальной системы GRS80, на которой основана система NAD73. Геодезические высоты, отсчитываемые относительно референц-эллипсоидов не имеют никакого отношения к полю силы тяжести. Последнее ведет к конфузу, который до сих пор часто встречается: когда в некоторых районах «вода течет вверх», если судить по геодезическим высотам (как мы поймем дальше, это справедливо и для общеземных эллипсоидов, центр которых совмещен с центром масс). Несмотря на это, некоторые местные эллипсоиды были созданы из расчета наилучшего расположения относительно местного геоида в том смысле, что в рамках выбранной территории их поверхность приближена к уровню моря (NAD37, Пуэрто-Рико). К примеру, при редуцировании расстояний в NAD27, поправки за высоту обычно именовались «поправками за уровень моря». Резюмируя, можно сказать, что референц-эллипсоиды являются математическим упрощением, которое позволяет строго вычислять геоцентрические, геодезические и географические координаты, таким образом, они не более чем основа горизонтальной поверхности относимости. Как утверждает Фишер (2004) «О. Кэфи объяснял мне использование эллипсоида только как математическую условность, для вычисления координат». Уровненные эллипсоиды В отличие от референц-эллипсоидов, которые получают в результате построения сетей триангуляции, глобальные, общеземные эллипсоиды создаются при помощи РСДБ (GRS80), методов спутниковой геодезии (WGS84) в сочетании с астрономическими и гравиметрическими измерения. РСДБ и спутниковая геодезия дают возможность точного измерения расстояний между точками, разделенными океанами. Полученные таким образом модели Земли являются глобальными - общеземными, они не подбираются конкретно под какую-то территорию. WGS-84 и GRS80 имеют такие размеры, что сумма квадратов отклонения от геоида для них минимальна. Цитируя Морица (2000 с,128) GRS80 была принята на XCII Генеральной Ассамблее IUGG в Канберре, в декабре 1979 г. следующим образом: «… поскольку GRS1967 уже не отражает с необходимой точностью форму, размеры и гравитационное поле Земли, рекомендуется заменить основу GRS1967 на GRS1980, основанную на уровенном эллипсоиде, определенном следующими параметрами: - большая полуось эллипсоида а=6 378137 м; - геоцентрическая гравитационная постоянная Земли GM- 3,986,005 x108 m3 s-2 - гармонический коэффициент J2= 108,263x 10-8 - угловая скорость Земли ? = 7292115 x10-11 rad s-1 Имеется значительное отличие уровенных эллипсоидов от референц-эллипсоидов. Если референц-эллипсоиды являются фигурой чисто геометрической, то уровенные эллипсоиды задаются набором как геометрических, так и физических параметров. GRS80 является уровенным эллипсоидом, (Мориц 2000) приведенные выше постоянные задают все свойства эллипсоида. К тому же, уровенные эллипсоиды (GRS80, WGS84) являются геоцентрическими, т.е. их центр совмещен с центром масс Земли. Необходимо, также, заметить, что центры эллипсоидов NAD83 и GRS80 на два метра не совпадают с центром ITRS, и WGS84 в данный момент подобрана таким образом, чтобы совпадать с ITRS. Уровенные эллипсоиды одновременно являются моделью фигуры Земли и ее гравитационного поля. Сомильяни (1929) вывел первую строгую формулу для нормальной силы тяжести, а в 1930 был принят первый международный уровенный эллипсоид. Он задавался, как: g0 = 9.78046{1+0.0052884sin2В - 0.0000059sin2(2В)} где g0 – ускорение свободного падения на расстоянии 6,378,137 м от идеальной Земли, B- геодезическая широта. Значение g0 называют теоретической силой тяжести или нормальной силой тяжести. Зависимость этой величины от геодезической широты связана как раз с фактом незамыкания нивелирных ходов на большие расстояния, особенно, протяженных с севера на юг (это выражено в больше степени, чем в направлении запад-восток). Для современных уровенных эллипсоидов GRS80 и WGS84 для вычисления нормальной силы тяжести используется формула Блейкли 1995