Источник:
http://www.profoptic.ru/articles/?id=30
Геодезия (греч. gedaisa, от ge – Земля и daio – делю, разделяю), наука об определении положения объектов на земной поверхности, о размерах, форме и гравитационном поле Земли и других планет. Это отрасль прикладной математики, тесно связанная с геометрией, математическим анализом, классической теорией потенциала, математической статистикой и вычислительной математикой. В то же время это наука об измерениях, разрабатывающая способы определения расстояний, углов и силы тяжести с помощью различных приборов. Основная задача геодезии – создание системы координат и построение опорных геодезических сетей, позволяющих определить положение точек на земной поверхности. В этом существенную роль играют измерения характеристик гравитационного поля Земли, связывающие геодезию с геофизикой, использующей гравиметрические данные для изучения строения земных недр и геодинамики. Например, в геофизике геодезические методы измерений применяются для исследования движений земной коры, поднятий и опусканий массивов суши. И наоборот, нарушения во вращении Земли, которые влияют на точность геодезической системы координат, отчасти могут быть объяснены физическими характеристиками литосферы.
Геодезические работы обычно выполняются государственными службами. В США созданием и поддержанием государственной геодезической сети занимается Национальная служба по исследованию океана при участии Министерства обороны и Национального управления по аэронавтике и исследованию космического пространства (НАСА). Международные геодезические исследования организуются и направляются Международной ассоциацией геодезии, действующей по инициативе и в рамках Международного геодезического и геофизического союза.
Геодезические работы ведутся на трех уровнях. Во-первых, это плановая съемка на местности – определение положения точек на земной поверхности относительно местных опорных пунктов для составления топографических карт, используемых, например, при строительстве плотин и дорог или составлении земельного кадастра. Следующий уровень включает проведение съемок в масштабах всей страны; при этом площадь и форма поверхности определяются по отношению к глобальной опорной сети с учетом кривизны земной поверхности. Наконец, в задачу глобальной, или высшей, геодезии входит создание опорной сети для всех остальных видов геодезических работ. Высшая геодезия занимается определением фигуры Земли, ее положения в пространстве и исследованием ее гравитационного поля.
Последнее имеет особенно большое значение, т.к. все геодезические измерения (за исключением расстояний) отчасти зависят от определения направления силы тяжести (совпадающего с направлением отвесной линии). Геодезические приборы (теодолит, используемый для измерения углов и направлений, и нивелир, измеряющий превышения) устанавливаются так, чтобы оси их установочных уровней были параллельны уровенной поверхности, всегда перпендикулярной направлению силы тяжести. Более того, сама форма земной поверхности (70% которой составляют акватории) в общем определяется конфигурацией уровенной поверхности, представляющей собой идеализированную поверхность океана; именно от нее производится отсчет высот конкретных точек (т.н. высота над уровнем моря). В гравитационном поле Земли под уровенной поверхностью понимают поверхность, в любой точке которой помещенное на нее тело остается в состоянии покоя. Конфигурация уровенной поверхности определяется путем измерения силы тяжести.
Относительное положение точек на поверхности Земли устанавливается путем измерения расстояний между ними (при условии, что каждый пункт геодезической сети может непосредственно наблюдаться с нескольких других пунктов). В настоящее время для определения взаимного расположения точек земной поверхности в качестве промежуточных точек используются искусственные спутники Земли, при этом измеряется расстояние между спутником и наземным пунктом. Поскольку эти измеренные расстояния не зависят от ускорения силы тяжести, может показаться, что гравитационное поле Земли не играет существенной роли в геодезических построениях. Однако космическая геодезия, хотя и дополняет традиционные наземные наблюдения, пока не может их заменить. Более того, орбиты самих искусственных спутников определяются гравитационным полем Земли, что опять-таки делает необходимым изучение силы тяжести.
Геодезия может рассматриваться в геометрическом и физическом аспектах. Геометрические задачи геодезии решаются методами съемки, т.е. измерениями и расчетами расстояний, углов и направлений. Физический аспект связан с измерениями силы тяжести. Геодезические измерения осложняются спецификой используемой системы координат, которая включает широту, долготу и высоту. Уровенные поверхности, по которым устанавливается высота точки, непараллельны вследствие изменений силы тяжести на земной поверхности, обусловленных особенностями рельефа (распределением гор, долин, впадин и пр.) и плотности слагающих Землю горных пород. Подобные же причины нарушают параллельность поверхностей, имеющих одинаковую широту или долготу. Кроме того, на результаты расчетов геодезических показателей, например координат точки, влияют погрешности измерений и используемой физической модели.
Прикладные аспекты геодезии.
Геодезические данные используются в картографии, навигации и землепользовании, например, для определения зоны затопления после сооружения плотины, местоположения буровых платформ на шельфе, точного положения государственных и разного рода административных границ и пр. Навигация и стратегические системы наведения в равной степени зависят от точности информации о положении цели и адекватности физических моделей, описывающих гравитационное поле Земли. Геодезические измерения используются в сейсмологии и при изучении тектоники плит, а гравиметрическая съемка традиционно применяется геологами при поисках нефти и других полезных ископаемых.
Развитие геодезии.
Геодезия возникла в глубокой древности. Ее развитию способствовал прогресс в естественных и точных науках, изобретение таких инструментов, как маятник и телескоп и др. Однако за последние полвека геодезия добилась больших успехов, чем за всю предшествующую историю, что связано с использованием данных, полученных с искусственных спутников, появлением электронно-вычислительных машин и электронных измерительных приборов. Современные компьютеры позволили проводить анализ большого объема информации, применять в геодезии новые математические разработки, придавшие новый импульс развитию теоретической геодезии параллельно с прогрессом математики и теории информации.
Методы съемки.
Положение точки на земной поверхности определяется с помощью трех координат: широты (центральный угол, образованный отвесной линией в данной точке с плоскостью экватора, отсчитывается к северу или к югу от экватора), долготы (угол между плоскостью меридиана, проходящего через данную точку, и плоскостью начального меридиана, за который условно принимается Гринвичский меридиан в Англии; отсчет ведется к западу или к востоку от начального меридиана) и высоты (расстояние по отвесной линии между данной точкой и некоторой уровенной поверхностью, например, средним уровнем моря).
Традиционно горизонтальные и вертикальная координаты рассматриваются порознь и исходные пункты устанавливаются для них отдельно. Такое различие продиктовано в основном практическими соображениями. Во-первых, основная задача геодезии – определить положение выбранных точек на поверхности Земли. При этом высотное положение меняется в гораздо более узких пределах, чем горизонтальное, и может определяться при помощи более простого математического аппарата. Во-вторых, классические способы измерения высот резко отличаются от тех, что применяются для определения показателей планового положения. Например, горизонтальные углы определяются гораздо точнее, чем вертикальные, при измерении которых возникают ошибки из-за рефракции световых лучей в атмосфере; поэтому измерение вертикальных углов играет меньшую роль в определении высот.
Однако теоретически не существует никаких препятствий для совместного определения вертикальных и горизонтальных (плановых) координат. Практически любые измерения высотных и плановых характеристик могут быть обобщены без введения каких-либо особых уровенных поверхностей. Именно такой способ применяется в т.н. пространственной, или космической, геодезии, где определение координат ведется с искусственных спутников и действительно нет методических различий в измерении планового положения и высоты. Хотя в конечном счете применение спутников может уменьшить потребность в разработке раздельных методов плановых и высотных измерений, различие подходов сохранится для решения многих практических задач.
Сеть высотных опорных пунктов.
Высотная привязка, или определение высотных отметок точек местности, в локальном и региональном масштабах или в масштабе страны осуществляется путем определения относительных высот (превышений) точек земной поверхности. Совокупность методов определения высот обозначается общим термином «нивелирование». При геометрическом нивелировании используется нивелир с цилиндрическим уровнем и зрительной трубой, ось которой устанавливается параллельно уровенной поверхности в данном месте приведением пузырька уровня на середину ампулы. Есть нивелиры с компенсатором, в которых ось зрительной трубы приводится в горизонтальное положение автоматически, с помощью компенсаторной призмы. Помещая нивелир между двумя точками (рис. 1) и производя отсчет по двум нивелирным рейкам, установленным вертикально в этих точках, определяют превышение между этими точками. Превышения также могут быть найдены непосредственным измерением вертикального угла (по отношению к горизонтальной плоскости или к зениту); такое измерение осуществляется с помощью теодолита, установленного в одной точке и направленного на другую точку. В таком случае необходимо знать расстояние между этими двумя точками. Этот метод известен как тригонометрическое нивелирование; он применяется чаще всего в условиях пересеченной местности с крутыми склонами, где геометрическое нивелирование неприменимо. Тригонометрическое нивелирование вследствие атмосферной рефракции уступает в точности геометрическому нивелированию.

Рис. 1. ГЕОМЕТРИЧЕСКОЕ НИВЕЛИРОВАНИЕ для определения превышений. Нивелир помещается примерно посредине между двумя проградуированными рейками в точках А и В. Визирный луч указывает отсчеты на рейках А' и B'. Разность длин отрезков АА' и BB' и является разностью высот точек А и В, т.е. превышением точки В над точкой А.
Высотное положение точек устанавливается посредством создания нивелирных сетей, состоящих из отдельных линий – нивелирных ходов; превышение по нивелирному ходу определяется как сумма превышений на станциях (между отдельными точками внутри хода); при этом превышение на станции получается как разность отсчетов на заднюю и переднюю нивелирные рейки. Нивелирные ходы прокладываются таким образом, что они начинаются и кончаются в одной и той же точке, образуя полигон; это помогает выявить погрешности измерений, т.к. сумма превышений для замкнутого нивелирного хода должна быть равна нулю и отличие ее от нуля указывает на сумму погрешностей. Поскольку конфигурация уровенных поверхностей зависит от гравитационного поля Земли (например, присутствие аномально большой массы в каком-либо месте вызывает заметное «вспучивание» уровенной поверхности), эти поверхности непараллельны. Из-за того, что визирный луч нивелира устанавливается параллельно уровенной поверхности в данном месте, измеренные превышения также зависят от силы тяжести. Для выполнения высокоточного нивелирования его данные должны дополняться гравиметрическими измерениями. Высота топографической поверхности над средним уровнем моря называется ортометрической высотой. Ортометрическая поправка рассчитывается с помощью гравиметрических наблюдений; введение этой поправки позволяет учесть непараллельность уровенных поверхностей.
Уровенная поверхность, ближе всего соответствующая среднему уровню Мирового океана (т.н. среднему уровню моря), называется поверхностью геоида (рис. 2). На суше эта поверхность представляет собой продолжение уровня моря под материками. Именно эта поверхность служит в качестве нулевой, от которой традиционно отсчитываются абсолютные высоты. Средний уровень моря определяется по данным систематических наблюдений (мониторинга) за приливами. Однако установление нулевой отметки высот по среднему уровню моря затруднено тем, что в региональных масштабах он не является строго выдержанным; поверхность моря отклоняется до нескольких десятков сантиметров от горизонтали под влиянием преобладающих ветров, течений, колебаний температуры и солености воды и атмосферного давления. В масштабе какой-либо одной страны нулевой уровень высот определяется на основании осредненных показателей многолетних замеров на нескольких водомерных постах. Однако, поскольку отклонения измеренного среднего уровня моря от истинной уровенной поверхности слишком велики, не представляется возможным принять единый глобальный нулевой уровень, базирующийся на замерах уровня моря.

ГЕОИД – фигура Земли, ограниченная уровенной поверхностью, совпадающей со средним уровнем Мирового океана при спокойном состоянии водных масс и продолженной под континентами. Общий земной эллипсоид представляет собой геометрическую фигуру, наиболее точно аппроксимирующую поверхность геоида. Угол между отвесной линией в данной точке и перпендикуляром к поверхности эллипсоида называется уклонением отвесной линии. Отклонения (положительные или отрицательные) геоида относительно эллипсоида называют ондуляциями геоида.
В США нивелирные сети подразделяются на сети 1-го, 2-го и 3-го классов в соответствии с необходимой точностью, расстоянием между отдельными пунктами, общей протяженностью и методом нивелирования. Наиболее точные сети 1-го класса представляют собой главную основу, устанавливающую единую систему высот для всей страны. Сети 2-го класса дополняют и сгущают более точные сети 1-го класса. В этих сетях расстояния между узлами и соседними пунктами, закрепленными на местности специальными марками и реперами, меньше, чем в сетях 1-го класса. Сети 3-го класса прокладываются для непосредственного высотного обоснования инженерно-технических проектов и крупномасштабных топографических съемок. Их точность определяется конкретными требованиями в каждом отдельном случае.
Сеть плановых опорных пунктов.
Создание геодезических плановых сетей основано на определении направлений, расстояний между пунктами и углов. Для измерения углов и направлений используется главным образом теодолит, основная рабочая часть которого, зрительная труба, вращается вокруг горизонтальной и вертикальной осей. Угол как в горизонтальной, так и в вертикальной плоскости измеряется угломерным кругом. Горизонтальный круг, по которому отсчитывают горизонтальные углы и направления, выравнивается с помощью специального цилиндрического уровня. Вертикальный круг служит для измерения углов наклона. Теодолит может использоваться также для измерения широты и долготы точки на местности. Для этого проводится наблюдение за звездами, занимающими вполне определенное положение на небесной сфере. Раньше для измерения расстояний использовались мерные ленты или рейки. Современный дальномер фиксирует время, за которое электромагнитные волны проходят расстояние между прибором, находящимся в одной точке, и отражателем, установленным в другой точке. Поскольку скорость распространения электромагнитных волн в воздушной среде известна, расстояние между точками определяется как произведение времени на скорость. В приборах для измерения расстояний, основанных на этом принципе, используются источники лазерного и микроволнового излучения. Теодолит и электронное дальномерное устройство монтируются в виде интегрального прибора, включающего устройства для электронного считывания показаний и автоматической коррекции погрешностей измерений.
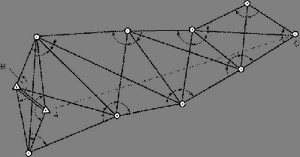
Построение геодезической опорной сети выполняется тремя методам: 1) триангуляции, когда плановое положение геодезических пунктов на местности определяется путем построения систем смежно расположенных треугольников, в которых измеряются углы, а длины сторон рассчитываются по длине хотя бы одной точно измеренной базисной стороны (или базиса) (рис. 3); 2) трилатерации – путем построения систем смежно расположенных треугольников и измерения их сторон; 3) полигонометрии – проложения на местности систем ломаных линий (полигонометрических ходов), в которых последовательно измеряются углы и длина каждого отрезка, соединяющего два пункта. В триангуляции и трилатерации для определения величины и формы треугольника достаточно знать величины двух углов и одной стороны или длины всех трех сторон. Длина сторон треугольников в плановых сетях обычно не превышает 15 км; в густонаселенных районах, крупных городах и других местах, где требуется сгущение сетей, они значительно короче. Для уменьшения ошибок измеряются все три угла, затем полученная сумма приводится к известной сумме углов треугольника (составляющей для сферических треугольников несколько более 180°). Плановые линейные характеристики сети получаются путем определения по крайней мере одной стороны треугольника; помимо этого в целях контроля выполняются и другие измерения. Расстояния между пунктами, расположенными на различных высотных отметках, приводятся к горизонтальной плоскости. Привязка геодезической сети, особенно опорных геодезических пунктов высокого класса, осуществляется измерением астрономического азимута, широты и долготы через определенные интервалы на местности.
Форма Земли не является идеально сферической; отклонения составляют примерно 1/300, в основном за счет того, что Земля сплющена у полюсов и приближается к сжатому эллипсоиду вращения (двухосный эллипсоид, полученный вращением эллипса вокруг короткой оси). Поэтому в качестве исходной уровенной поверхности при построении опорной геодезической сети используется поверхность референц-эллипсоида, короткая ось которого параллельна оси вращения Земли, а размеры выбраны таким образом, чтобы он максимально совпадал с поверхностью геоида для данной территории. Все расстояния и направления, измеренные на поверхности Земли при определении планового положения точки, пересчитывают (редуцируют) для перенесения на поверхность референц-эллипсоида. Например, в измеренные величины расстояний между точками необходимо внести поправку на их превышение над поверхностью референц-эллипсоида, которое соответствует сумме истинного превышения поверхности геоида в данном месте и ортометрической высоты (т.е. измеренной строго по вертикали над поверхностью геоида). Подобным же образом углы и направления, или азимуты, измеренные в горизонтальной плоскости, пересчитывают для получения соответствующих им величин на поверхности референц-эллипсоида, т.к. отвесная линия не совпадает с перпендикуляром к поверхности референц-эллипсоида. Поэтому вводится поправка за уклонение отвесной линии (рис. 2). Кроме того, существует расхождение между координатами (широтой и долготой) точки, полученными с помощью астрономических наблюдений (астрономические координаты), и геодезическими координатами соответствующей точки на поверхности эллипсоида. Отметим, что и положение поверхности геоида и направление отвесной линии учитываются в определении планового и высотного положения опорных пунктов сети. Это еще раз свидетельствует о важности исследований гравитационного поля Земли.
Исторически сложилось так, что на территории наиболее крупных стран поверхность референц-эллипсоида совмещалась с действительной поверхностью Земли в каком-либо одном пункте опорной сети, для чего в этом пункте определялось уклонение отвесной линии. «Расположение» эллипсоида в теле Земли затем устанавливалось измерением астрономического азимута (направления на какой-либо соседний пункт) и угла, который этот азимут образует с направлением на астрономический зенит, а затем соотнесением этих величин с геодезическим азимутом и зенитным расстоянием данного пункта на поверхности эллипсоида. С помощью такой процедуры достигается параллельность короткой оси эллипсоида и оси вращения Земли. Различия конфигурации эллипсоида и геоида определяются превышением (разностью отметок их поверхностей) в «исходном пункте». Наконец, для закрепления опорной плановой сети определяются размер и форма (сжатие) эллипсоида с помощью методов, обычно используемых для расчетов формы Земли.
Таким образом, для одной точки эллипсоида устанавливалось точное положение относительно соответствующей точки на физической поверхности Земли. На основе значений относительной высоты геоида, ортометрической высоты и астрономических координат на поверхность эллипсоида проектировалось положение других точек земной поверхности. Для уточнения положения опорных пунктов сети на промежуточных пунктах проводились дополнительные определения астрономического азимута. На практике исходные пункты геодезической сети выбирались таким образом, чтобы обеспечить хорошее соответствие поверхности эллипсоида опорной сети данной страны или крупного географического региона. При этом центр эллипсоида не обязательно совпадал с центром масс Земли. Поэтому для различных районов мира используются несколько различающиеся плановые опорные сети. Однако с появлением орбитальных искусственных спутников Земли значительно упростились измерения ускорений силы тяжести в глобальных масштабах и, следовательно, повысилась точность определения положения поверхности геоида и точность ее соответствия поверхности референц-эллипсоида. Более того, наблюдая за движением спутников из определенных точек на поверхности Земли, определяют геоцентрические координаты этих точек. Множество наземных станций, для которых найдены эти координаты, обеспечивают жесткую основу геодезической сети. Плановое положение других пунктов сети определяется обычными методами. Если удастся принять общий земной эллипсоид для всех геодезических сетей, это позволит избежать сложных и чреватых ошибками пересчетов при переходе от одной региональной сети к другой.
Геометрическая форма эллипсоида описывается с помощью экваториального радиуса и сжатия, представляющего собой отношение разности длин большой и малой полуосей эллипсоида к большой полуоси. Эти параметры обычно определяются совместно; раньше для этого использовались результаты измерений наземных плановых сетей, а теперь – измерений со спутников. Первое определение размеров Земли было осуществлено Эратосфеном из Александрии в 3 в. до н.э., который считал, что Земля имеет форму шара. Он знал, что в городе Асуан Солнце стоит выше всего (практически в зените) в полдень в день летнего солнцестояния. В тот же день он измерил зенитное расстояние (угол между направлением на зенит и направлением на Солнце) в Александрии и нашел, что он равен примерно 7,2°. Зная это и приблизительное расстояние между двумя городами (по меридиану), он определил радиус Земли с ошибкой менее 15%. Дуговые расстояния измерялись с помощью астрономических наблюдений китайскими учеными в 8 в. и арабскими – в 9 в.
В Западной Европе попытки определить размер Земли с использованием более точных методов были предприняты только в 17 в., когда было снаряжено несколько экспедиций, в задачи которых входило измерение длины дугового градуса методом триангуляции. Вместо того, чтобы измерять высоту Солнца, они наблюдали звезды; им удалось провести измерения с погрешностью не более нескольких процентов. Было отправлено две экспедиции, одна в Лапландию, а другая в Перу, чтобы проверить утверждение И.Ньютона о том, что следствием вращения Земли должно быть увеличение ее экваториального радиуса (и, следовательно, сжатие ее у полюсов). Эти экспедиции позволили решить вопрос в пользу представлений И.Ньютона и опровергли более ранние результаты, не подтвердившие его точку зрения. Другим очень важным способом определения сжатия Земли явилось измерение ускорения силы тяжести вблизи полюсов и на экваторе. Если Земля действительно имеет сплюснутую у полюсов форму, то сила тяжести должна возрастать от экватора к полюсам, т.к. при этом уменьшается расстояние до центра масс Земли.
Французский математик А.Клеро (1713–1765) установил зависимость изменения силы тяжести от геометрической формы (сжатия), впервые выявив тесную связь между геометрическими и физическими параметрами Земли. Третий способ измерения сжатия земного эллипсоида (использующийся и сегодня) – наблюдение за движением по орбитам искусственных спутников Земли. Если бы Земля обладала идеально симметричным распределением плотностей в недрах, то орбита любого спутника представляла бы собой эллипс, никогда не изменяющий ни положения, ни ориентировки. Однако расширение Земли у экватора вызывает изменения орбиты (прецессию и нутацию), исследования которых используются для расчетов сжатия Земли и определения параметров референц-эллипсоида.
Плановая опорная сеть в США образована рядом меридиональных и широтных полигонометрических ходов, связывающих между собой пункты, координаты которых определяются из спутниковых наблюдений. Такая трансконтинентальная сеть ходов, помимо основной цели – давать плановую основу для геодезической съемки, служит также для мониторинга дрейфа континентов и движения плит земной коры.
Определение положения точек с помощью спутников.
Появление искусственных спутников Земли произвело переворот в методах геодезии и значительно повысило точность навигации и определения положения точек и объектов на поверхности Земли. Большое преимущество, которое дает геодезии использование искусственных спутников, состоит в том, что спутник может синхронно наблюдаться с нескольких наземных станций, что позволяет определять их взаимное расположение. Сам спутник при этом может играть пассивную роль (например, отражая луч лазера, посланный с наземной станции, обратно на ту же станцию) или активную роль (непрерывно осуществляя передачу радиосигнала). На первых этапах развития космической геодезии сигналы подавались в виде вспышек света, которые фотографировались на фоне звезд одновременно с нескольких наземных пунктов, находящихся вне непосредственной видимости. Положение спутника на фотографии относительно опорных звезд давало возможность определить точное направление на него с данной станции наблюдения. Спутниковые системы позволяют наблюдателю, где бы он ни находился, точно определять свое местонахождение (например, Система глобального определения местоположения – Global Positioning System, GPS, использующая созвездие навигационных спутников NAVSTAR).
Обычно измеряют расстояние между наземным пунктом и спутником и скорость изменения этого расстояния при прохождении спутника. Расстояния рассчитывают, исходя из времени, которое затрачивает электромагнитный сигнал (лазерная вспышка или радиоимпульс) на прохождение пути от спутника до принимающей станции, при условии, что скорость движения сигнала известна. Вводятся поправки за атмосферную задержку сигнала и рефракцию. Скорость изменения расстояния между спутником и принимающей станцией определяется по величине наблюдаемого доплеровского сдвига частоты – изменения частоты сигнала, поступающего со спутника. Еще одна группа спутниковых наблюдений основана на принципе интерферометрии (т.е. наложения волн), когда радиоимпульс принимается в двух пунктах на земной поверхности и определяется время его запаздывания в одном пункте по отношению к другому. По величине этой задержки и известной скорости распространения волны с учетом угла подхода (который рассчитывается на основе известных параметров орбиты спутника) вычисляется расстояние между двумя пунктами. Наблюдения нескольких спутников позволяют также точно определить направление базисной линии, соединяющей наземные станции.
Различные методы наблюдений позволяют определять абсолютное и относительное положение объектов на земной поверхности. При определении абсолютного положения (например, расстояния) используются не менее трех спутников, находящихся на существенно различающихся орбитах, т.к. положение каждой точки земной поверхности изменяется по трем осям – с севера на юг, с востока на запад (плановые координаты) и вверх-вниз (высотная координата). Поскольку весьма существенно при этом время наблюдения, то обычно требуется еще и четвертый спутник, чтобы компенсировать разницу в точности определения времени по часам, установленным на борту спутников и на наземной станции. Определение относительного положения пункта на земной поверхности требует одновременного наблюдения нескольких спутников (на практике обычно не менее четырех) с двух (или более) наземных станций.
Чтобы перейти к геоцентрической системе координат, необходимо знать элементы орбиты спутника в этой системе, любые погрешности в определении которых автоматически влекут за собой неточности в определении положения станции наблюдения. Эти погрешности могут быть уменьшены путем осреднения наблюдаемых величин за несколько дней, недель или месяцев. Многие систематические погрешности в расчетах элементов орбиты примерно в одинаковой степени отражаются на всех станциях наблюдения и взаимно уничтожаются при определении взаимного положения этих станций, поэтому относительные положения обычно определяются с большой точностью. В зависимости от числа одновременно работающих принимающих станций и одновременно наблюдаемых спутников можно получать определенные различия между принимаемым и передаваемым сигналами; это позволяет исключить влияние неизвестных факторов.
Наиболее перспективной космической системой, служащей для решения геодезических задач, является система глобального определения местоположения, которая начала разрабатываться в начале 1970-х годов на основе существовавших ранее навигационных систем в военно-морских и военно-воздушных силах США. Эта система стала исключительно точным инструментом для решения прикладных задач геодезии, геофизики и землепользования.
GPS состоит из трех частей: 18 рабочих искусственных спутников, размещенных симметрично на круговых орбитах, системы управления и пользователей. Каждый спутник в этой системе снабжен микропроцессором для обработки данных, приемником и передатчиком для связи с наземной системой управления и для передачи функциональных сигналов пользователям, несколькими атомными часами для определения точного времени. Энергоснабжение спутника осуществляется двумя большими солнечными батареями. Система управления объединяет операторов и наблюдателей станций слежения, рассредоточенных по всей планете. Они определяют орбиты спутников, постоянно контролируют функционирование их систем и точность хода часов и передают информацию на спутники для ретрансляции ее пользователям, имеющим специальный приемник, преобразующий сообщения со спутников в информацию о координатах. Приемное устройство состоит из антенны, источника энергии, процессора с несколькими каналами ввода для приема различных сигналов со спутника, записывающего устройства для хранения обработанных данных и приборов, дающих возможность считывания информации пользователем.
Системы координат.
Широта какой-либо точки на поверхности Земли определяется по отношению к экватору (или, что то же самое, по отношению к оси вращения Земли, которая перпендикулярна экватору). Измерив высоту звезды над горизонтом и зная склонение этой звезды, наблюдатель может определить широту пункта своего местонахождения, если ему известна ориентировка оси вращения планеты по отношению к звездам.
Долгота определяется относительно начального меридиана, который проходит через пункт вблизи Гринвичской обсерватории в Англии. Угол между этим меридианом и тем, на котором находится объект, определяется по времени, которое требуется конкретной звезде, чтобы «переместиться» по суточной параллели (однако это движение видимое, поскольку в действительности вращается Земля) от одного меридиана до другого.
На точность измерений широты и долготы влияют колебания скорости вращения Земли и направления земной оси относительно звезд и земной коры. Именно изменение ориентировки земной оси по отношению к небесной сфере приводит к изменению наблюдаемого склонения небесного светила, а по отношению к земной коре это изменение влияет на широту, определяемую наблюдателем. Наиболее сильное влияние оказывает общая прецессия, период которой составляет примерно 25 700 лет. При вращении земная ось, подобно оси волчка, описывает конус; в результате этого через 12 850 лет Северный полюс земной оси будет направлен в точку небесной сферы, отстоящую примерно на 47° от Полярной звезды. Прецессия и другие движения меньшей амплитуды (нутация) обусловлены гравитационным воздействием на Землю Солнца, Луны и других близлежащих планет. Изменение положения Северного полюса (т.е. точки пересечения земной оси с поверхностью Земли) связано с физическими свойствами земных недр, в частности, с упругостью, наличием жидкого ядра и неоднородным распределением масс. Положение Северного полюса Земли также изменяется во времени. С периодичностью ок. 1,2 года он описывает почти правильную окружность, диаметр которой (измеренный на поверхности Земли) составляет приблизительно 4–5 м.
Все наземные системы координат так или иначе привязаны к Северному полюсу и к начальному меридиану. После того, как было принято международное соглашение относительно этих исходных параметров, все страны используют единую систему координат. Истинное положение Северного полюса было определено Международной службой движения полюсов, в которую входит ряд обсерваторий; широты этих обсерваторий постоянно поверяются астрономическими наблюдениями. В работе Службы принимает также участие Международное бюро времени в Париже. В 1988 вместо этих двух международных организаций была создана Международная служба вращения Земли, использующая постоянные наблюдения за вращением Земли (продолжительность суток и движение полюсов) с многочисленных станций и обсерваторий, применяющих традиционные астрономические методы, РСДБ, лазерную локацию спутников и Луны и т.д. Международная служба вращения Земли ведает единой системой координат и определяет положение Земли в пространстве для решения геодезических, астрономических и геофизических прикладных задач, а также следит за соотношением всемирного времени (мерой которого является вращение Земли) и атомного, измеряемого атомными часами. Чтобы обеспечить совпадение этих двух систем измерения времени, атомные часы периодически юстируют на несколько секунд.
Измерительные устройства.
Наиболее распространенный прибор для измерения силы тяжести – гравиметр, используемый для относительных измерений, т.е. разности значений силы тяжести в двух пунктах. Основным элементом гравиметра является горизонтальное коромысло, на одном конце которого размещен груз, а на другом находится опора, относительно оси которой коромысло может поворачиваться под действием наклонно расположенной пружины. Один конец пружины крепится к коромыслу вблизи точки размещения груза, второй – к жесткому элементу корпуса прибора. Если в каком-либо пункте указатель шкалы прибора, связанный с положением груза, стоит на нуле, то в другом пункте в связи с изменением силы тяжести (и, соответственно, положения груза) показание на шкале прибора будет отличаться от нуля. Это показание шкалы и определяет разность значений силы тяжести между двумя пунктами. Достоинствами таких гравиметров являются малые размеры и высокая точность (до 0,02 миллигала, мГал).
Для получения действительного значения ускорения силы тяжести в любом пункте относительные измерения в заданном пункте связывают с данными абсолютных измерений силы тяжести в этом пункте с помощью баллистического гравиметра, в котором измеряется время падения тела под действием силы тяжести. Расстояние, пройденное этим телом в процессе падения, измеряется лазерным интерферометром, а время падения – высокоточным электронным устройством. Точность измерения баллистическими гравиметрами достигает 0,01 мГал. Для проведения абсолютных измерений силы тяжести требуется большое количество вспомогательного оборудования, поэтому их нецелесообразно проводить при обычных геодезических съемках. Большинство баллистических гравиметров размещается в стационарных лабораториях, однако существуют и транспортабельные устройства, имеющие приемлемые уровни точности измерения.
Международная гравиметрическая стандартная сеть по состоянию на 1971 включала 10 гравиметрических станций для абсолютных измерений и 1854 пункта для относительных измерений силы тяжести. Эта сеть является основой для проведения большого количества региональных гравиметрических съемок с точностью 0,1–0,2 мГал. Хотя статические гравиметры позволяют получить наиболее точные значения, их использование в полевых условиях требует значительных затрат труда и времени.
Применение гравиметров на подвижных основаниях затруднено главным образом тем, что прибор не способен ощутить разницу между ускорением силы тяжести и возникающим при этом инерционным (кинематическим) возмущающим ускорением (например, вследствие вертикальных перегрузок при движении автомобиля, корабля или самолета). Тем не менее существуют подобные системы, способные обеспечить точность гравиметрических измерений порядка нескольких миллигал. В них используются усовершенствованные наземные гравиметры либо комплекты акселерометров, измеряющих величину ускорения по всем направлениям. Кинематическая составляющая ускорения вычитается из общего значения, для чего система осуществляет постоянное дифференцирование пройденного расстояния по времени, а полученные скорости после последующего дифференцирования дают искомые значения ускорений. Кроме того, появляется возможность ввести поправки на действие таких редко учитываемых факторов, как ускорение Кориолиса и центростремительное ускорение.
Для успешного функционирования транспортабельных гравиметрических устройств необходимо использовать высокоточные современные системы навигации. В аэрогравиметрических съемках обычно используются бортовые радиолокационные системы с радиолокационными или лазерными альтиметрами (высотомерами). Для достижения необходимой точности учитываются также данные, полученные со спутниковой системы GPS. При измерении градиента силы тяжести (величины изменения ускорения силы тяжести на очень малых расстояниях) обычно пренебрегают учетом положения и ускорения самого аппарата-носителя, однако при этом используются более сложные измерительные приборы. Существующие мобильные системы проведения гравиметрических измерений либо находятся в стадии опытной разработки, либо (как в случае гравиметрической системы, размещаемой на вертолете) используются исключительно в геофизических исследованиях.
Важную роль в совершенствовании измерений параметров гравитационного поля Земли сыграло использование радиолокационных альтиметров, размещаемых на борту орбитальных спутников. В принципе, спутниковая альтиметрия достаточно проста: расстояние от спутника до поверхности океана определяется с помощью электронных устройств, измеряющих время, за которое радиоволны проходят это расстояние и обратный путь до бортового приемного устройства после отражения от поверхности океана. Скорость распространения сигнала, умноженная на половину полученного временного отрезка, дает искомое значение высоты. Уровень поверхности океана (приблизительно соответствующий поверхности геоида) относительно центра Земли или относительно поверхности некоего эллипсоида рассчитывается как разность между высотой орбиты спутника (которая постоянно определяется расположенными вокруг земного шара станциями слежения) и значениями измеренной высоты полета спутника над поверхностью океана. Таким образом, при использовании спутниковой системы измерений для определения высотного положения поверхности океана (геоида) на значительной части его площади потребуется несколько месяцев. Поскольку ок. 70% общей площади поверхности Земли приходится на океан, значительная часть ранее не известных данных о гравитационном поле Земли (аппроксимированной в виде геоида) была получена в процессе первых же витков полета специализированного спутника.
Если же известна конфигурация конкретной границы (в данном случае уровенной поверхности) поля силы тяжести, то определение значений силы тяжести становится чисто математической задачей. Первые спутниковые альтиметры имели точность ок. 1 м, а более современные – несколько сантиметров. Основное ограничение точности измерений при использовании спутниковой альтиметрии определяется параметрами горизонтального разрешения при сканировании поверхности океана и высокой скоростью движения спутника. Еще одно ограничение налагает неполнота наших знаний об изменении скорости распространения электромагнитных волн в различных слоях атмосферы. Чтобы воспользоваться преимуществами высокой точности, которую дают современные альтиметры, необходимо добиться сопоставимой точности в определении орбиты спутника и степени расхождения между поверхностью геоида и поверхностью океана, возмущаемой воздействием ветров, течений, температур и других факторов. Фактически многие полеты спутников, выполнявших альтиметрические наблюдения, специально планировали для получения данных об океанических течениях путем повторных замеров высоты по определенным маршрутам. Поверхность геоида, являющаяся постоянной величиной, при этом исключалась из результатов наблюдений, учитывались только изменения уровня океана по отношению к поверхности геоида, позволяющие судить о течениях и других процессах.
Методика.
Гравитационное поле Земли принято разделять на две части: нормальное гравитационное поле и остаточное аномальное поле. В физической геодезии оперируют в основном с аномальным гравитационным полем. Основное преимущество такого подхода состоит в том, что аномальное поле гораздо слабее действительного гравитационного поля Земли и поэтому его характеристики легче определить. Нормальное гравитационное поле характеризуется четырьмя параметрами: общей массой Земли; формой и размерами эллипсоида, наиболее близко соответствующего геоиду в глобальном масштабе; скоростью вращения Земли. Его определение вытекает из условия, что поверхность эллипсоида – это уровенная поверхность в нормальном гравитационном поле, а поверхность геоида представляет собой уровенную поверхность в действительном гравитационном поле (нормальное поле объясняет также существование негравитационной, центробежной, силы, которая возникает вследствие вращения Земли вокруг своей оси). При этом предполагается, что центр нормального эллипсоида (или референц-эллипсоида) совпадает с центром масс Земли. В любой точке разность высот геоида и референц-эллипсоида, называемая ондуляцией геоида, прямо пропорциональна возмущающему потенциалу (потенциал силы тяжести – одна из важнейших характеристик гравитационного поля Земли). Таким образом, определение аномального гравитационного поля (путем гравиметрических измерений) позволяет определить положение поверхности геоида по отношению к эллипсоиду и отсюда – форму Земли. Если нам известна форма геоида, то известно и направление силы тяжести, которое в каждой точке перпендикулярно к поверхности геоида. Следовательно, можно найти уклонение отвесной линии, т.е. угол между направлением силы тяжести и перпендикуляром к поверхности эллипсоида.
В математической физике существуют т.н. граничные, или краевые задачи, формулируемые примерно следующим образом. Если изменения некоторой величины, например возмущающего потенциала, подчиняются какому-то закону и эта величина (или связанная с ней) принимает определенное значение на какой-то граничной поверхности, то можно определить значение этой величины в любой точке пространства. В геодезии сила тяжести определяется прямыми измерениями; таким образом задача состоит в том, чтобы определить возмущающий потенциал на земной поверхности и над ней. Однако в геодезии краевая задача осложняется тем, что граничная поверхность (в данном случае физическая поверхность Земли), определяемая относительно геоида, представляет собой искомую величину, которая определяется в последнюю очередь; поэтому это еще одна неизвестная величина, входящая в задачу. С теоретической точки зрения, это одна из самых трудных проблем в геодезии, для которой получены пока только приближенные решения.
Ирландский математик Дж.Стокс в 1849 первым решил геодезическую краевую задачу при условии, что ускорение силы тяжести известно в любой точке поверхности геоида (рассматриваемой в данном случае как граничная поверхность). Однако, определить силу тяжести на всей земной поверхности очень нелегко, а измерять силу тяжести на поверхности геоида на суше вообще невозможно. Единственно возможное решение состоит в том, чтобы рассчитать ускорение силы тяжести для геоида, используя данные измерений на земной поверхности и вводя поправку за аномалию высоты. Этот метод требует также учета гравитационного воздействия масс земной коры, находящихся между топографической поверхностью и поверхностью геоида.
В конце 1950-х годов советский геодезист М.С.Молоденский нашел решение, пригодное для любой произвольной поверхности (в т.ч. топографической); эта поверхность может быть описана по гравиметрическим данным. Хотя это решение также приближенное, оно представляет шаг вперед, т.к. не требует знания плотностной структуры верхней части земной коры, как это требовалось в решении Стокса. В обоих случаях величина ускорения силы тяжести вблизи той точки, где должна быть определена поверхность геоида, оказывает гораздо более сильное влияние, чем в более удаленных областях. Отсюда следует, что требования к точности измерений силы тяжести в глобальном масштабе могут быть не столь строгими.
Другие аспекты геодезических исследований.
Благодаря применению современных приборов и методов измерений появилась возможность вносить коррективы в систему геодезических координат. Однако такие уточнения довольно редки, поскольку система координат должна быть довольно жесткой, и все же в некоторых случаях, например, при изучении землетрясений, гравиметрические и чисто геодезические работы учитывают и временной аспект событий.
В 1960-х годах, когда очень активно велись исследования Луны, большинство задач, связанных с определением местоположения, навигацией и картографированием, решались геодезическими методами. Сейчас совершенно ясно, что методики, разработанные для изучения Земли, могут быть использованы на любой другой планете, хотя конечно, в каждом случае это будет сопряжено со специфическими трудностями.
Резюме
| Биография
| Реферат
| Библиотека
| Ссылки
|
| Индивидуальный раздел
ДонНТУ >
Портал магистров ДонНТУ


