УДК 622.831.
Обоснование возможности применения метода конечных элементов при расчете напряженно-деформированного состояния дискретизированных пород
Д.т.н. Касьян н.н., к.т.н. НЕГРЕЙ С.Г. аспирант МОКРИЕНКО В.Н. студ. КУРДЮМОВ Д.Н. г. Донецк, Украина.
На основании результатов расчетов с использованием положений механики грунтов и моделирования методом конечных элементов обоснована возможность применения МКЭ при исследовании напряженно-деформированного состояния окружающего массива и установлении механизма выдавливания подстилающих пород из-под охранных сооружений.
Проблема и ее связь с практическими задачами. Анализ современных тенденций подземной разработки угольных пластов Украины позволяет сделать вывод о том, что с увеличением глубины ведения горных работ всё большее распространение находят схемы отработки выемочных участков с поддержанием подготовительных выработок вслед за очистным забоем. Вместе с тем, это сопряжено с проблемой обеспечения их эксплуатационного состояния позади лавы в зонах влияния очистных работ и установившегося горного давления, а также необходимостью разработки эффективных способов и средств охраны выемочных выработок.
В 60-70% случаях неудовлетворительное состояние выработок, поддерживаемых позади лавы, обусловлено интенсивными смещениями пород почвы. Многосложность процесса пучения пород почвы определяет широкий спектр способов борьбы с этим явлением. И, как показывает практика, одних лишь способов предотвращения пучения пород почвы в усложняющихся условиях отработки пластов недостаточно, и для обеспечения устойчивости выработки необходимо рассмотрение вопросов ее поддержания и охраны в комплексе. Причем правильно выбранные способ и средства охраны являются наиболее результативным путем снижения затрат на крепление и поддержание выработок [1]. Очень часто сами средства охраны (бутовые полосы, БЖБТ, литые полосы и др.), а именно схемы их установки и размещение относительно выработки, являются причинами интенсивного пучения пород почвы, и эти сооружения играют роль штампа, из-под которого выдавливаются породы в полость выработки [2, 3].
Таким образом, разработка способов и определения их параметров должны предусматривать комплекс исследований напряженно-деформированного состояния (НДС) окружающего массива и установление механизма выдавливания подстилающих пород из-под охранных сооружений с целью обеспечения безремонтной эксплуатации выработки.
Результатами лабораторных исследований доказана эффективность применения способа охраны жесткими сооружениями с компенсационными полостями [4], сущность которого состоит в том, что за счет схемы установки вдоль выработки жестких опор в форме прямоугольного параллелепипеда с ориентацией их большей боковой гранью перпендикулярно продольной оси выработки и оставлением между ними компенсационных полостей, под действием горного давления выдавливающие силы перенаправляются в эти полости, чем достигается уменьшение смещений пород почвы выработки и обеспечивается ее эксплуатационное сечение без необходимости проведения ремонтных работ.
Дальнейшие исследования в этом направлении и разработка рекомендаций по применению предложенного способа требуют уточнения его параметров. На этом этапе нельзя ограничиться только лабораторным моделированием, которое даёт возможность получения широкого диапазона решений, но со значительной степенью схематизации объектов изучения. А так как этих недостатков лишены аналитические методы, которые позволяют получить решения с наибольшей степенью общности и в широких диапазонах изменения условий, представляется необходимым привлечение численных методов в достижении поставленных целей.
В последнее время широкое распространение получили численные методы, в частности метод конечных элементов (МКЭ), который является основой многих коммерческих программ, которые применяются при расчете напряженно-деформированного состояния в различных средах, причем при идентификации параметров модели исследуемого материала с реальными условиями с помощью МКЭ с достаточно большой достоверностью можно моделировать дискретные среды. Кроме того, адекватность результатов численного моделирования может быть определена сопоставлением их с результатами расчетов известными апробированными методами.
В связи с этим целью настоящей работы является установление адекватности результатов численного моделирования методом конечных элементов и аналитических расчетов методом угловых точек, который основан на использовании положений механики грунтов и сыпучих сред, при исследовании процесса выдавливания подстилающих пород из-под прямоугольного штампа.
Основная часть. На первом этапе исследований с использованием решения Н.А. Цытовича методом угловых точек [5] определялись сжимающие напряжения в подстилающих породах на различных глубинах под центрами и под серединами длинных сторон загруженных внешней нагрузкой прямоугольников размерами 1´1, 1´2, 1´3, 1´5 и 1´10м.
Максимальные сжимающие напряжения под центром загруженного прямоугольника (рис. 1) определялись из выражения
![]() , (1)
, (1)
где Ko– угловой коэффициент для центральных точек;
Р– интенсивность равномерно распределенной нагрузки, МПа.
Угловой коэффициент Ko из выражения (1) определяется отношением напряжения в рассматриваемой точке массива от действия внешней пригрузки к величине прикладываемой к прямоугольнику нагрузки и является ни чем иным, как коэффициентом концентрации напряжений от действия этой силы.
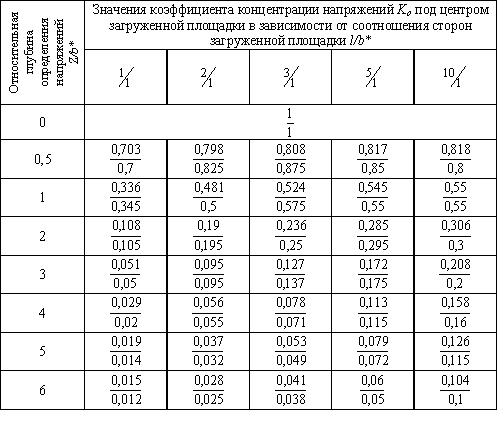
Значения коэффициента определялись в соответствии с таблицей 3.2 [5] и интерполяцией в зависимости от размеров прямоугольной площадки и глубины определения напряжений и представлены в таблице 1. В графической форме зависимость изменения данного показателя с глубиной приведена на рисунке 2.

Рисунок 1– Схема по определению сжимающих напряжений в подстилающем массиве от действия внешней нагрузки
Таблица 1– Результаты расчетов коэффициента концентрации напряжений Ko, полученные методом угловых точек (значения в числителе) и МКЭ (значения в знаменателе)
На втором этапе исследований данная задача была решена методом конечных элементов.
Была создана модель почвы горной выработки в системе аналитического проектирования SolidWorks [6], и решена задача статики в линейной постановке посредством пакета конечно-элементного анализа CosmosWorks [7]. Общий вид конечно-элементной модели показан на рисунке 3.
Исходными данными для моделирования приняты типичные условия для глубоких шахт украинского Донбасса, отрабатывающие пласты пологого падения [8]: модуль упругости Е=1,3×108 кг/м2, объёмная масса g= 2,3 т/м3, пределы прочности на одноосное сжатие sсж=24,5 МПа и одноосное растяжение sр=2,5 МПа, коэффициент Пуассона µ= 0,25.
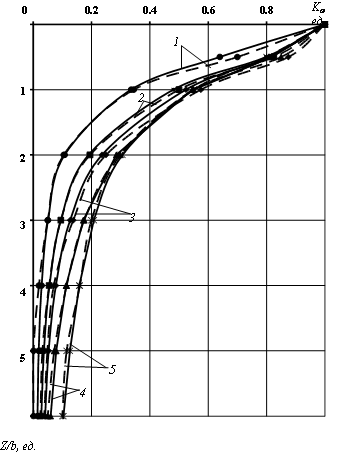
Рисунок
2– Графики зависимости коэффициента концентрации напряжений в подстилающих
жесткую прямоугольную опору породах в зависимости от расстояния до внешней
нагрузки, полученная по результатам расчетов методом угловых точек (![]() ) и конечно-элементного моделирования (
) и конечно-элементного моделирования (![]() ), при различном соотношении сторон
основания опоры (1– при соотношении 1:1, 2– 2:1, 3– 3:1, 4– 5:1 и 5– 10:1)
), при различном соотношении сторон
основания опоры (1– при соотношении 1:1, 2– 2:1, 3– 3:1, 4– 5:1 и 5– 10:1)

Рисунок 3– Общий вид конечно-элементной модели по определению напряжений в подстилающих породах от действия внешней нагрузки на жесткую опору с основанием прямоугольной формы
Условия на границах моделируемого участка оставались неизменными на всех этапах исследования. Размер массива горных пород был принят 21×30×15м. Ширина опоры b по оси ОХ (рис. 2) на всех этапах моделирования была принята 1м, а ее длина l изменялась от 1 до 10м. Таким образом, была отработана серия моделей с соотношениями сторон прямоугольника 1:1, 2:1, 3:1, 5:1 и 10:1.
На верхнюю грань параллелепипеда была приложена внешняя нагрузка по прямоугольной площадке размерами b×l.
В результате конечно-элементного моделирования были получены распределения напряжений в подстилающих породах при различных соотношениях сторон основания штампа. В таблице 1 приведены значения коэффициента концентрации напряжений в подстилающем массиве по оси, проходящей через центр загруженной площадки, которые определялись с помощью МКЭ. Зависимость коэффициента концентрации напряжений от расстояния до внешней нагрузки с учетом параметров опоры, полученная по результатам конечно-элементного моделирования представлена на рисунке 2.
Из рисунка 2 следует, что с увеличением площади опоры величина напряжений в подстилающих породах и глубина действия внешней нагрузки увеличивается.
Сравнение результатов расчетов двумя методами позволило установить, что отклонение конечно-элементного решения от решения методом угловых точек не превышает 9%. Данное обстоятельство указывает на их сходимость и возможность применения МКЭ в данной постановке при решении пространственных задач для дискретных сред, находящихся в начальном (ненарушенном) или конечном (стабилизированном) статическом состоянии. В этих случаях под действием внешней нагрузки массив будет находиться в предельном напряженном состоянии, когда зависимость между деформациями и напряжениями линейна.
Выводы. Таким образом, результатами проведенных исследований доказана возможность применения численного моделирования методом конечных элементов при исследовании физических процессов в подстилающих охранное сооружение породах.
Рекомендованная литература:
1. Технология, механизация и организация проведения горных выработок / Б.В. Бокий, Е.А. Зимина, В.В. Смирняков, О.В. Тимофеев. Учебник для вузов. 3-е изд., перераб. и доп. М., Недра, 1983.– 264с.
2. Прогнозування зближень порід контуру, проведених слідом за лавою підготовчих виробок на пологих пластах: Автореф. дис... канд. техн. наук: 05.15.02 / О.Ю. Стулішенко; Донец. нац. техн. ун-т. — Донецьк, 2002. — 17 с.
3. Негрей С.Г., Мокриенко В.Н. Об особенностях пучения пород почвы выемочных выработок в условиях пласта m3 шахты им. В.М.Бажанова // Проблеми гірничої технології: Матеріали регіональної науково-практичної конференції, Красноармійський індустріальний інститут ДонНТУ, 2008.– С. 97-102.
4. Мокриенко В.Н. Параметрирование нового способа охраны выемочной выработки с использованием метода эквивалентных материалов // Збірник наукових праць НГУ. 2010 №34 Т.1. С 166-173.
5. Цытович Н.А. Механика грунтов (краткий курс): Учебник для вузов. - 3-е изд., доп.- М.: Высш. школа, 1979.- 272 с.
6. Алямовский А.А. SolidWorks/COSMOSWorks. Инженерный анализ методом конечных элементов. – М./ ДМК Пресс, 2004. – 432с.
7. Сухов С.А. Основы моделирования в SolidWorks: методические указания- Ульяновск УлГТУ, 2007-48с.
8. Справочник (кадастр) физических свойств горных пород. Под ред. Н.В. Мельникова, В.В. Раевского, М. М. Протодьяконова- М. «Недра» 1975.- 219с.