
Грохочение – это основная стадия для разных производственных процессов, горной промышленности, где в основном вся продукция подвергается процессу грохочения на протяжении производственного цикла.Вибрационные грохота способны осуществлять процедуру отбраковки и нести тяжелую нагрузку системы приводов и из-за свойств сырья. Кроме того, это оборудование соответствует требованиям рынка, так как имеет более низкие затраты и срок поставки, более высокую безопасность и доступность. Другое важное требование - более высокая производительность, которая является результатом большой просеивающей поверхности, следовательно, вибрационные грохоты шире. Известно, что увеличение ширины грохота значительно осложняет проектирование вибрационного оборудования. В этом кратком обзоре с одной стороны теоретические и практические знания необходимы для установления правильных размеров просеивающей поверхности для гарантии работы и с другой стороны математические инструменты, такие как численное моделирование по методу конечных элементов, которые необходимы для обеспечения структурной устойчивости. Данная работа представляет собой введение о применении и разработке высокопроизводительного вибрационного грохота. Переменные такие как удар, частота, ускорение, живое сечение сита и их влияние на эффективность грохочения будет кратко рассмотрено так же как собственная частота, форма колебаний, статические и динамические воздействия и их влияние на структурное проектирование.
Вибрационные грохота в основном собираются в прочную раму, состоящую главным образом из стальных листов, называемых коробом грохота. Короб грохота опирается на цилиндрические винтовые пружины или резиновые виброизоляторы и комплектуется системой привода и ситом (-ами) (одно- или многодечные). Иногда создается изоляция также используемая для уменьшения коэффициента передачи динамических нагрузок на опорную конструкцию. Вообще, вибрационные грохоты идентифицируются по ширине и длине просеивающей поверхности.
У вибрационных грохотов в основном два типа движения: круговое (наклонные или круговые вибрационные грохоты) и линейное (горизонтальные или линейные вибрационные грохоты).
В круговых вибрационных грохотах частица перемещается круговыми движениями, задаваемыми системой привода и наклоном деки. Амплитуда равна радиусу круга, образованного при движении короба (ход равен диаметру).
Линейные вибрационные грохоты были разработаны, чтобы уменьшить вертикальные габаритные размеры, необходимые круговым грохотам и обеспечить лучший контроль за обезвоживанием. Однако, помимо обезвоживания, линейные вибрационные грохоты также широко используются при классификации. В отличие от круговых вибрационных грохотов, линейные в состоянии транспортировать материал без помощи силы тяжести, образуемый угол вектора возбуждения обычно равен 450 с поверхностью деки. Амплитуда равна половине длины траектории (ход равен целой длине).
Высокая эффективность грохочения достигается при правильном определении размеров просеивающей поверхности, правильном выборе ее типа, правильном выборе амплитуды и рабочей частоты при грохочении материала. Частица должна двигаться по просеивающей поверхности, не попадая в одну и ту же ячейку, но и не перескакивая через несколько ячеек. В таблице 1 приведена рекомендуемая частота в зависимости от размера ячеек для линейных вибрационных грохотов (Chaves and Peres 2003).

Соотношение между силой привода (FC) и вибрирующим весом короба называют фактором грохочения (К). Он должен быть в пределах от 3g до 5g – обычно 4g – (HBL 2004). Известно, что центробежная сила - функция вибрирующей массы (m) и центробежного ускорения (aC); и что центробежное ускорение - функция амплитуды (a) и рабочей частоты, выраженной в Гц (w) или об/мин (N):

В этом пункте важно подчеркнуть, что правильное определение фактора грохочения так же как рабочей частоты и амплитуды основано на эмпирической информации, связанной с характеристикой просеиваемого материала.
Относительно систем приводов вибрационного грохота для круговых вибрационных грохотов больше всего распространена одновальная с неуравновешенными массами (2 балансира). Ширина вибрационного грохота ограничена длиной вала 2500 мм. По этому параметру стоимость становится невозможной из-за размера балансира, механической прочности/измерения размеров вала, расстояния между деками и т.д. Распределительный вал (4 балансира — ход от жесткого привода) имеет аналогичные ограничения одновальных по отношению к двухвальным. Однако, последний грохот движется линейно из-за встречного вращения валов. Вибраторы могут использоваться для возбуждения круговых или линейных движений, но их конструкция (электродвигатель, соединенный с балансиром), препятствует их применению в высокопроизводительных грохотах. Они требуют более высоких возбуждающих сил, следовательно больших масс балансиров и двигателей. В отличие от первых, у системы приводов возбудителя нет ограничений по ширине, означая, что большинство высокопроизводительных грохотов (более широкие грохоты) используют возбудители в качестве системы приводов (Iizuka 2006).
Главная цель измерений величин напряжения - экспериментальное определение величин напряжения в любой точке анализируемой структуры. Возможно, что величина напряжения, хода и ускорения, определенного числовым моделированием, отличаются от реальных величин, таким образом экспериментальный анализ необходимо оптимизировать с помощью модели для расчета методом конечных элементов, уменьшая это различие.
Величины напряжения связаны с мостом Уитстона так, когда анализируемый составляющая нагружена отдельными блоками перевозимого оборудования, электрическое сопротивление изменяет величину напряжения, вызывающую неустойчивость в мосте. Эта неустойчивость выражена в изменении напряжения и пропорциональна напряжению составляющей.
Для правильного выбора величины напряжения, факторы как окружающие условия (главным образом тепловой), необходимую точность, исходные условия, затраты, металлическую чувствительность сплава, длину деформации напряжения на координатной сетке и другие нужно рассмотреть. Связанный с конструктивной формой величины напряжения, три типа - основные: одноосный (применяемый, когда основные показателями известны с точностью ±5°); прямоугольная розетка или X розетка (для применений, вовлекающих двуосные условия напряжения с известными основными показателями) и розетка R (используемая в применении с двуосными условиями напряжения с неизвестными основными показателями). В данной работе только R розетка 0°/45°/90° будет глубоко проанализирована, потому что это в значительной степени используется в контрольно-измерительной аппаратуре вибрационных грохотов (Хоффмэнн 1989).
Главное напряжение (e1, e2, e3) может быть определено с помощью круга Мора (Measurements Group 1990), поскольку углы круга Moра - дважды физические углы инструментованной поверхности и совмещение круга Moра с осью розетки R: (см. рис. 1),
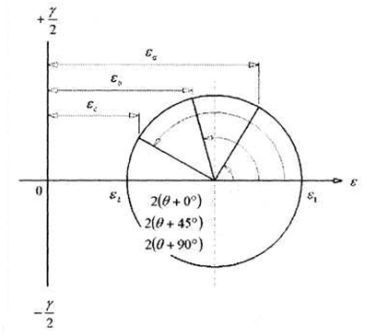

Управление системой уравнения, основные напряжения могут быть определены в зависимости от напряжения величины напряжений (ea, eb, ec):

Предполагая, что проанализированный материал - однородный по своему составу и изотропный по своим механическим свойствам и использовании линейных отношений между напряжением и напряженностью, Закон Гука применительно к плоской деформации напряжения, может использоваться для определения главного напряжения (a1, a2, c3) через главные деформации так же, как напряжение Мизеса.

Использование напряжения Мизеса (a1) широко используется в методе конечных элементов, потому что это уменьшает шестимерные измерения в простой скаляр.
Разные механические проекты, такие как вибрационные грохоты, требуют расчета при помощи созданных технических рисунков программным обеспечением CAD и структурного анализа в программном обеспечении CAE. Стадии проектирования (CAD и CAE) производят повторяющийся процесс, который может быть заявлен до изготовления оборудования или даже до изготовления опытного образца, значительно уменьшая время и затраты проекта (Iizuka 2002). Для подтверждения числового моделирования применимы экспериментальные методы и инструменты. Программное обеспечение CAD, используемое для создания геометрической модели, было Solid Edge V20; и программное обеспечение CAE, обычно применяемое при структурном анализе, было MSC.FEA 2007rl, которое обеспечивало взаимодействие между MSC.Patran (препроцессор и постпроцессор) и MSC.Nastran (решающее устройство).
Данная программа проанализировала грохот R-TE 4 000*11 000 высокой производительности (4 000мм ширина и 11 000 мм длина): модульный линейный вибрационный грохот с одной декой, которую возбуждают 6 возбудителей. Эта машина была разработана и изготовлена Haver & Boecker Latinoamericana Syncrude Ltd (применение нефтяного песка). Основной материал - низкие температурные стальные пластины с модулем Юнга 2.1*1011Н/м2; числом Пуассона 0.3, плотностью 7.85* 103 кг/м3, гомогенных и изотропных.
Таблица 3 представляет некоторые технические данные, связанные с вибрационным грохотом R-TE 4000* 11000.
Таблица 4 представляет результаты числового модального анализа (игнорирующий формы колебаний твердого тела — частотой собственных колебаний менее чем 4.00 Гц).
Модальный анализ является исконным в разработке вибрационного оборудования. Как только эксплуатационная частота приближается к собственной частоте, возрастают динамические усилия (явления резонанса). Эксплуатационная частота R-TE 4000*11000 составляет 11.67 Гц (700 об/мин), и самая близкая собственная частота составляет 12.48 Гц; исторические экспериментальные данные, выполненные при помощи VFD (Двигатель Переменной частоты), показали, что текущего различия 0.8lГц достаточно, чтобы избежать эффектов резонанса.
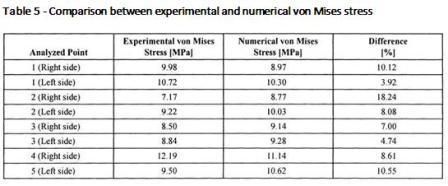
Второй проанализированный результат - сравнение критического напряжения в между числовым моделированием и экспериментальными измерениями. За исключением точки 2 (Правая сторона), таблица 5 показывает, что у всех других точек есть различия ниже или приблизительно 10 % (среднее различие 8.91 %), которое является приемлемым пределом, подтвержденным моделью конечного элемента. Различие, представленное в точке 2, следовало из существующего звука сигнала, который был установлен во время цифрового фильтрования сигнала.
В большей части проанализированных точек (62,5 %) напряжение Мизеса в числовой модели выше, чем экспериментальные вследствие того, что поверхностные элементы относящиеся к числовому моделированию, имеют поведение оболочки. Однако, в экспериментальных измерениях, плоская деформация напряжения засвидетельствована. Последние два комментария об измерениях величины напряжения: хотя эта техника проявила чрезвычайную точность, позволяющую проектировать любую части вибрационного короба, это требует чрезвычайной точности, главным образом в создании условий, соединении и шагах сварки элементов так, чтобы были получены достоверные результаты. Правильная типовая норма после Теоремы Найквиста, чтобы избежать совмещения названий, правильного выбора фильтров (низкий проход, в случае грохотов), чтобы избежать утечки является также важными требованиями в измерениях величины напряжения.
Относительно максимальных величин напряжения они ниже пределов, предусмотренных определенными стандартами к бесконечной усталости металла. Критерии Мизеса, оказалось, были практичны и полезны в структурном анализе.
У данной работы есть также практическое применение: вибрационный грохот R-TE 4000*11000 установлен и работающий в Syncrude LTD. (Область Реки Атабаски, Альберта, Канада), действующий более чем 40 000 часов без конструктивных проблем.
Bathe, Klaus-Jiirgen, 1982. Finite element procedures in engineering analysis. New Jersey: Prentice-Hall.
Chaves, A.P., and Peres, A.E.C., v.3 2003. Teoria e Prdtica do Tratamento de Minerios. Sao Paulo: Signus.
Cook, Robert D., 1989. Concepts and applications of finite element analysis. Madison: University of Wisconsin.
Faco, eds 1994. Manual de Britagem. Sorocaba: Allis — Mineral Systems.
Haver & Boecker Latinoamericana (HBL), 2004. Seminario Nash+HBL. Monte Mor: HBL
Hoffmann, Karl, led., 1989. An Introduction to measurements using strain gauges. Alsbach-Hahnlein: Hottinger Baldwin Messtechnik GmbH.
Iizuka, Eduardo Kenji, 2002. Construcao de model os de elementos finitos e andlise experimental de estruturas mecdnicas. Campinas: Universidade Estadual de Campinas - Mechanical Engineering Dept.
lizando o metodo dos elementos finitos e experimentalmente por extensometria. Campinas: Universidade Estadual de Campinas - Mechanical Engineering Dept.
Measurements Group, 1990. Technical Note — 77V 575—Strain gauge rosettes. Measurements Group. MSC, 2003. NAS120—Linear static, normal model and buckling - Analysis using MSC.Nastran and MSC.
Patran. Santa Ana: MSC.Software Corporation.