 ,
(1)
,
(1)
Важнейшим неотъемлемым элементом рациональной разведки и разработки месторождений полезных ископаемых является геометризация недр, включающая в себя совокупность полевых наблюдений, измерений, вычислений и графических построений, проводимых с целью геометрического изображения форм залежей, условий их залегания, пространственного распределения свойств полезного ископаемого и процессов, которые происходят в недрах.Для графического моделирования показателей свойств полезного ископаемого, распределение которых не является постоянным по любому направлению, используются так называемые поверхности топографического порядка, под которыми понимают поверхности неправильного вида, не имеющие определенного геометрического закона своего образования. К ним относятся как физически существующие поверхности, так и условные (скрытые) поверхности.
Геометризация качественных показателей углей позволяет в наглядной форме охарактеризовать закономерности распределения классификационных показателей марки угля и степень их изменчивости. При геометризации качественных показателей углей одной из ;основных задач является установление однородных площадей и построение границ марочного состава углей.
Для построения границ марочного состава углей применим метод тренд-анализа, в котором закономерности (тренды) изменения классификационных показателей марки угля выявляются путем сглаживания или аппроксимации данных опробования. При этом скрытые топографические поверхности классификационных показателей марки угля, сравниваются с математическими поверхностями, формы которых задаются различными математическими уравнениями. Аппроксимирующие математические поверхности показателей марки угля описываются полиномами вида [1, 2, 3]:
 ,
(1)
,
(1)
где Z – значение классификационного показателя марки в точке опробования;
X, Y – координаты точек опробования;
am – коэффициенты полинома;
m – степень полинома.
Метод полиномиального построения математических моделей поверхностей сталкивается с проблемой определения оптимальной степени описывающих полиномов, так как не всегда более высокая степень полинома дает положительный результат. С увеличением степени полинома не только усложняется сама поверхность, но и усиливается влияние случайных колебаний свойств, что может отрицательно сказаться на надежности аппроксимации.
На рис. 1, в качестве подтверждения вышесказанного, показаны границы марок угля Д, ДГи Г по пласту l3 шахты "Привольнянская", построенные по толщине пластического слоя у на основании данных геологической разведки пласта и с помощью полиномов различных степеней методом тренд-анализа.
Полином второй степени Полином третей степени
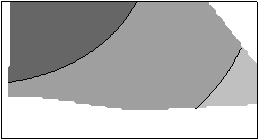
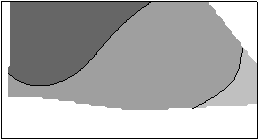
Полином пятой степени По данным геологической разведки


Рис. 1.Результаты построения границ марок угля по пласту l3 шахты
"Привольнянская"
Как видно из рис. 1, в рассматриваемом случае при построении границ различных
марок угля наибольшую сходимость с результатами геологической разведки
имеют границы марок угля, построенные с помощью описывающих полиномов
II> и
III степеней, а не более высокой
С целью установления оптимальной степени описывающих полиномов при построении границ марочного состава углей методом тренд-анализа был произведен сравнительный анализ различных математических поверхностей со скрытыми топографическими поверхностями, построенными по данным геологической разведки.
Для проведения анализа были использованы данные опробования качественного состава угля по девяти пластам действующих шахт Донбасса. При построении границ марочного состава угля использовались следующие основные классификационными параметрами марки угля:
Соответствие аппроксимирующего полинома скрытой топографической поверхности, построенной по данным опробования, к математической поверхности оценивалось методом наименьших квадратов:
![]() (2)
(2)
где Ziист – значение классификационного показателя марки угля, определенное по данным опробования в i- той точке;
Ziвыч – вычисленное значение классификационного показателя марки угля аппроксимирующей поверхности в в i- той точке опробования.
В таблице 1 для различных шахтопластов приведены результаты сравнительного анализа математических поверхностей, описанных полиномами различных степеней, со скрытыми топографическими поверхностями, которые были построены по данным опробования угольных пластов. При построении границ марочного состава угля по отдельным качественным показателям использовались различные объемы выборок, представленные в таблице 1 величиной n.
В качестве критериев выбора степени полинома аппроксимирующей функции использовались коэффициент корреляции и дисперсия.
Табл. 1. Результаты сравнительного анализа математических поверхностей, описанных полиномами различных степеней
|
Показатель |
Степень полинома |
|||
|
1 |
2 |
3 |
4 |
|
|
1 |
2 |
3 |
4 |
5 |
|
пласт l6 шахта "Ясиновская Глубокая" |
||||
|
Ro, n=16, среднее значение 1,85% |
||||
|
Коэффициент корреляции |
0,91 |
0,96 |
0,99 |
0,99 |
|
Дисперсия |
0,08 |
0,06 |
0,02 |
0,02 |
|
Vdaf, n=130, среднее значение 15,1% |
||||
|
Коэффициент корреляции |
0,58 |
0,58 |
0,61 |
0,61 |
|
Дисперсия |
2,76 |
2,75 |
2,67 |
2,67 |
|
y, n=77, среднее значение 7 мм |
||||
|
Коэффициент корреляции |
0,57 |
0,67 |
0,71 |
0,71 |
|
Дисперсия |
5,11 |
4,84 |
4,58 |
4,54 |
|
RI, n=29, среднее значение 6 единиц |
||||
|
Коэффициент корреляции |
0,68 |
0,71 |
0,84 |
0,85 |
|
Дисперсия |
6,79 |
6,48 |
5,08 |
6,79 |
|
пласт l11 шахта №13 "бис" |
||||
|
Vdaf, n=72, среднее значение 20,7% |
||||
|
Коэффициент корреляции |
0,61 |
0,63 |
0,63 |
0,63 |
|
Дисперсия |
1,46 |
1,43 |
1,29 |
1,22 |
|
y, n=55, среднее значение 13,2 мм |
||||
|
Коэффициент корреляции |
0,55 |
0,59 |
0,59 |
0,59 |
|
Дисперсия |
3,23 |
2,98 |
2,84 |
2,80 |
|
пласт k5 шахта "Горняк-95" |
||||
|
Vdaf, n=52, среднее значение 22,1% |
||||
|
Коэффициент корреляции |
0,61 |
0,62 |
0,64 |
0,65 |
|
Дисперсия |
1,91 |
1,92 |
1,90 |
1,96 |
|
y, n=18, среднее значение 14,1 мм |
||||
|
Коэффициент корреляции |
0,44 |
0,48 |
0,48 |
0,48 |
|
Дисперсия |
3,07 |
2,95 |
2,65 |
2,65 |
|
пласт l11 шахта "Калиновская Восточная" |
||||
|
Vdaf, n=72, среднее значение 22,5% |
||||
|
Коэффициент корреляции |
0,66 |
0,66 |
0,67 |
0,67 |
|
Дисперсия |
1,45 |
1,42 |
1,31 |
1,29 |
|
y, n=55, среднее значение 17,4 мм |
||||
|
Коэффициент корреляции |
0,67 |
0,67 |
0,68 |
0,69 |
|
Дисперсия |
3,16 |
3,37 |
3,00 |
2,80 |
|
пласт d4 участок "Красноармейский Западный № 2-3" |
||||
|
Ro, n=103, среднее значение 1,40% |
||||
Окончание табл.1
|
1 |
2 |
3 |
4 |
5 |
|
Коэффициент корреляции |
0,79 |
0,79 |
0,79 |
0,79 |
|
Дисперсия |
0,12 |
0,10 |
0,10 |
0,10 |
|
Ro-расч, n=595, среднее значение 1,30% |
||||
|
Коэффициент корреляции |
0,75 |
0,75 |
0,75 |
0,75 |
|
Дисперсия |
0,07 |
0,06 |
0,06 |
0,06 |
|
y, n=454, среднее значение 11 мм |
||||
|
Коэффициент корреляции |
0,02 |
0,03 |
0,18 |
0,19 |
|
Дисперсия |
2,47 |
2,16 |
2,07 |
2,03 |
|
Vdaf, n=564, среднее значение 26,4% |
||||
|
Коэффициент корреляции |
0,77 |
0,78 |
0,78 |
0,78 |
|
Дисперсия |
1,69 |
1,62 |
1,61 |
1,60 |
|
Qsdaf, n=120, среднее значение 8524 кал/г |
||||
|
Коэффициент корреляции |
0,61 |
0,64 |
0,64 |
0,64 |
|
Дисперсия |
82,9 |
81,6 |
78,3 |
76,9 |
|
пласт m3 шахта им. В.Н. Бажанова |
||||
|
Vdaf, n=212, среднее значение 24,4% |
||||
|
Коэффициент корреляции |
0,85 |
0,85 |
0,85 |
0,85 |
|
Дисперсия |
1,58 |
1,54 |
1,51 |
1,50 |
|
y, n=171, среднее значение 18 мм |
||||
|
Коэффициент корреляции |
0,74 |
0,74 |
0,75 |
0,75 |
|
Дисперсия |
3,48 |
3,32 |
3,23 |
3,20 |
|
пласт m9 шахта им. В.Н. Бажанова |
||||
|
Vdaf, n=272, среднее значение 34,3% |
||||
|
Коэффициент корреляции |
0,77 |
0,77 |
0,83 |
0,83 |
|
Дисперсия |
1,25 |
1,10 |
1,08 |
1,06 |
|
y, n=229, среднее значение 21 мм |
||||
|
Коэффициент корреляции |
0,75 |
0,75 |
0,76 |
0,76 |
|
Дисперсия |
3,32 |
3,29 |
3,21 |
3,14 |
|
пласт l3 шахта "Привольнянская" |
||||
|
Vdaf, n=139, среднее значение 42,3% |
||||
|
Коэффициент корреляции |
0,00 |
0,15 |
0,23 |
0,23 |
|
Дисперсия |
2,47 |
2,43 |
2,31 |
2,30 |
|
y, n=105, среднее значение 7 мм |
||||
|
Коэффициент корреляции |
0,40 |
0,40 |
0,41 |
0,41 |
|
Дисперсия |
3,23 |
3,21 |
3,20 |
3,20 |
|
Ro, n=46, среднее значение 0,55% |
||||
|
Коэффициент корреляции |
0,05 |
0,15 |
0,16 |
0,16 |
|
Дисперсия |
0,04 |
0,03 |
0,02 |
0,02 |
|
Ro-расч, n=105, среднее значение 0,55% |
||||
|
Коэффициент корреляции |
0,04 |
0,11 |
0,11 |
0,11 |
|
Дисперсия |
0,03 |
0,02 |
0,02 |
0,02 |
|
пласт i41 шахта №"17-17 "бис" |
||||
|
Vdaf, n=13, среднее значение 36,6% |
||||
|
Дисперсия |
3,38 |
3,15 |
2,99 |
- |
|
y, n=6, среднее значение 15,5 мм |
||||
|
Дисперсия |
0,08 |
0,03 |
- |
- |
|
Ro, n=8, среднее значение 0,9% |
||||
|
Дисперсия |
0,09 |
0,08 |
- |
- |
Как видно из таблицы 1, при построении границ марочного состава углей методом тренд-анализа целесообразно использовать описывающие полиномы II и III степеней, т.к. построенные с их помощью математические поверхности имеют наибольшую сходимость со скрытыми топографическими поверхностями, построенными по данным опробования пласта.
Полученные выводы подтверждаются материалами исследований и других авторов: в работе [3, 4] наилучшие функции, аппроксимирующие исходные геологические данные, это полиномы третьей степени, в работе [2] – полином второй степени.
Выводы:
1. Построение границ марочного состава углей с достаточной степенью надежности можно производить методом тренд-анализа, в котором закономерности (тренды) изменения классификационных показателей марки угля выявляются путем сглаживания или аппроксимации данных опробования.
2. Увеличение степени полинома аппроксимирующей математической поверхности показателей марки угля не повышает надежность аппроксимации.
3. При построение границ марочного состава углей методом тренд-анализа целесообразно использовать описывающие полиномы II и III степеней.
Библиографический список
1. Дэвис Дж.С. Статистический анализ данных в геологии: Пер. с англ. В 2 кн. – М.: Недра, 1990. – Кн.2. – 427 с.: ил.
2. Забигайло В.Е., Лукинов В.В., Пимоненко Л.И., Сахневич Н.В. Тектоника и горно-геологические условия разработки угольных месторождений Донбасса. – Киев: Наукова думка, 1994. – 152 с.
3. Поротов Г.С. Математические методы моделирования в геологии: Учебник. – СПб, 2006. – 223 с.
4. Поротов Г.С. Основы статистической обработки материалов разведки месторождений. – Л.: ЛГИ, 1985. – 97 с.