ЗАСТОСУВАННЯ МЕТОДУ КЛАСТЕРНОГО АНАЛІЗУ ДЛЯ РОЗПОДІЛУ ЗАПАСІВ ВУГІЛЛЯ ЗА МАРКАМИ

В.В. Мирний, к.т.н., проф., І.В. Філатова

Донецький національний технічний університет

Геометризація якісних показників є однією із задач геолого-маркшейдерської служби підприємств, на основі рішення якої стає можливим в наочній формі охарактеризувати закономірності розподілу класифікаційних показників марок вугілля та ступінь їхньої мінливості. При цьому вирішуються питання виділення однорідних площ і побудови границь марочного складу вугілля.

Розрізнено геометризовані показники класифікації вугілля утворюють зони, які перекриваються (часто на значних площах), що не дає можливості візуально визначити границі конкретних марок. Тому в багатьох випадках розмежування марочного складу вугілля виконується досить умовно зі значними похибками. Між тим, віднесення вугілля до тієї чи іншої марки згідно з державними стандартами [6] повинно виконуватись на основі сумісного (інтегрального) обліку всіх обумовлених класифікаційних показників.

Побудова контурів марок вугілля являє собою важливу виробничу задачу на різних етапах освоєння родовищ (підрахунок запасів вугілля, облік стану та руху запасів, визначення шляхів виробничого призначення сировини, заповнення облікових форм і ін.). В зв’язку з цим, виникає нагальна потреба у розробці методики побудови границь марок вугілля на основі математичних методів, які дозволяють узагальнити облік всіх класифікаційних показників.

Для рішення поставленої задачі, на наш погляд, найбільш оптимальним є застосування кластерного аналізу, тобто математичної процедури багатомірного аналізу, яка дозволяє на основі великої кількості показників, що характеризують ряд об’єктів, згрупувати їх у класи (кластери) таким чином, щоб об’єкти одного класу були більш однорідними і подібними у порівнянні з об’єктами інших класів [1-5, 7]. Виходячи з цього, сукупність якісних показників, яка належать до різних марок вугілля, можна розділити на групи у відповідності з задачею кластеризації. При цьому, якісні показники описуються чисельними виразами і обчислюються відстані між ними, які будуть виражені в евклідовій або в інших метриках. Перевага такого аналізу полягає в тому, що розбивка об’єктів виконується не за одним параметром, а за набором ознак. Для рішення поставленої задачі можуть бути використані методи кластеризації, які ґрунтуються на використанні матриць подібності, оцінюванні функцій цільності статичного розподілу, евристичних алгоритмах перебору, програмуванні та ін.

В запропонованій роботі виконані деякі дослідження класифікаційних показників пласта k₅ шахти "Гірник-95" (Центральний Донбас) на основі кластерного аналізу. Показники є даними опробування, які зібрані в повному обсязі зі справ розвідувальних свердловин і за результатами опробування в гірничих виробках. За результатами підготовки даних створена база даних по пласту k₅ шахти "Гірник-95", яка включає основні характеристики: номера свердловин або точок опробування, планові координати, відмітки поверхні, відмітки точок перетину свердловин з пластом, результати лабораторних досліджень класифікаційних показників марки вугілля (середнього показника відбиття вітриніту R_о, виходу летких речовин V^daf і товщини пластичного шару y).

Попереднє виявлення кластерів і оцінювання їх числа

Попереднє виявлення кластерів й оцінювання їх кількості ґрунтується на дослідженні поводження варіаційного ряду відстаней між різними точками [1-5]. Для рішення поставленої задачі застосовується теорія кластерного аналізу [1-5, 8].

Формування основного варіаційного ряду (ОВР) і його дослідження. Досліджувана множина Х представлена вісімнадцятьма свердловинами:

заданих p числовими ознаками (середнім показником відбиття вітриніту R_o, виходом летких речовин V^daf та товщиною пластичного шару y):

Значення кожного класифікаційного показника нормовано відносно середнього значення за парами ознак: виходом летких речовин V^daf і товщиною пластичного шару y;  виходом летких речовин V^daf і середньому показнику відбиття вітриніту R_o; товщиною пластичного шару y і середньому показнику відбиття вітриніту R_o.

За міру подібності двох елементів прийнята евклідова відстань [1-5, 8]:

Елементами х_i й у_i є пари класифікаційних показників, що характеризують марочний склад вугілля (для дослідження приймаються вище перелічені пари ознак).

Обчисливши по формулі (3) відстані між всіма взятими парами елементів множини Х, одержимо множину дійсних чисел. Після впорядкування елементів множини за зростанням одержимо основний варіаційний ряд (ОВР):

Структура досліджуваних множин відображена у поводженні варіаційних рядів, для яких будуються гістограми (рис. 1). Ідея основного підходу до рішення поставленого завдання кластеризації базується на аксіомі: якщо множина Х складається з k (k³2) віддалених один від одного кластерів, то щільність імовірності ОВР має хоча б один локальний мінімум, що спостерігається на його гістограмі.

З рис. 1 видно, що варіаційні ряди мають локальні мінімуми, отже, множина неоднорідна й включає кілька кластерів.

Для встановлення статистичної значимості локального мінімуму в інтервалі  визначені найближчі локальні максимуми в інтервалах  й . Перевірку гіпотези Н_о про сталість щільності ймовірності виконано в проміжку . Підраховано число спостережень , що потрапили в інтервал  і число рівних проміжків гістограми , що втримуються в інтервал . Гіпотеза Н_о перевіряється за критерієм згоди [4] і зведена до перевірки того, що з  інтервалів число точок дорівнює , для чого обчислена статистика:

де n_j – число спостережень, що потрапили в j-проміжок інтервалу ;

    – число рівних проміжків гістограми.

Число спостережень підраховано за формулою:

Зафіксовано рівень значимості a і по таблиці розподілу c² [6, 9] зі  ступенями свободи знайдене значення. Якщо , то гіпотеза Н_о відкидається й розглянутий локальний мінімум гістограми вважається статистично значимим. Якщо , то гіпотеза Н_о не відкидається й локальний мінімум є статистично не значимим.

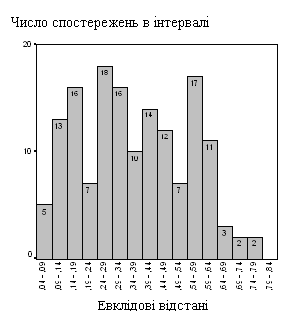
Розглянемо встановлення локальних мінімумів на прикладі створеної гістограми евклідових відстаней для пари ознак виходу летких речовин V^daf і товщини пластичного шару y (рис. 1а).

    а                                                                               б

   в

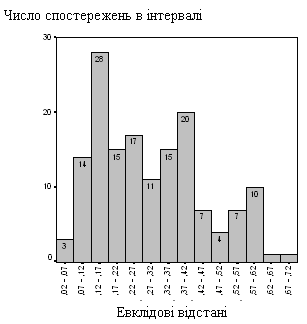
Рис. 1. Гістограми ОВР евклідових відстаней показників

а –  за ознаками V^daf й y

б – за ознаками V^daf й R_o

в – за ознаками y й R_o

Гістограма ОВР евклідових відстаней між цими ознаками має чотири локальних мінімуми на інтервалі : [0,04;0,09), [0,19;0,24), [0,49;0,54), [0,69;0,74). Число спостережень n_j, які зафіксовані в даних інтервалах, складає 5, 7, 7, 2. Найближчі локальні максимуми в інтервалах  для наведених вище локальних мінімумів складають: [0,04;0,19), [0,19;0,29), [0,49;0,64), [0,69;0,79). Число спостережень, які попали в ці інтервали складає : для першого інтервалу 5+13+16=34, для другого – 7+18 =25, для третього – 7+17=24 та останнього – 2. Число інтервалів : 3, 2, 2, 2.

Встановлення локальних мінімумів для гістограми евклідових відстаней між виходом летких речовин V^daf і середнім показником відбиття вітриніту R_o та між товщиною пластичного шару y і середнім показником відбиття вітриніту R_o (рис. 1 б, в) виконується аналогічно. Результати перевірки гіпотези Н_о (про сталість щільності ймовірності) при 5-процентному рівні значимості (a=0,05) наведені у таблиці 1.

Таблиця 1 - Перевірка статистичної значимості локальних мінімумів ОВР

Аналіз даних, наведених у табл. 1, показав, що при такому рівні значимості всі локальні мінімуми не є статистично значимими, так як виконується умова . Тому множина Х або однорідна, або складається із кластерів, що перетинаються або близько розташовані друг до друга.

Проведені дослідження переднього виявлення кластерів, які застосовані на дослідженні поводження основних варіаційних ряді відстаней між парами класифікаційних показників по пласту k₅ шахти "Гірник-95" (Центральний Донбас), стосовно [6], свідчить про те, що запаси вугілля по цьому пласту належать до різних марок, площі розподілу яких або перетинаються, або близько розташовані друг до друга.

Для оцінювання числа кластерів (марок по пласту k₅ шахти "Гірник-95") проведемо аналіз множини Х на основі дослідження додаткових варіаційних рядів – мінімальних і максимальних відстаней, елементи яких відповідають різним парам точок. Для отриманих евклідових відстаней сформовані дві множини і :

де – елементи мінімальних евклідових відстань між ознаками;

    – елементи максимальних евклідових відстань між ознаками.

Видаливши з отриманих множин  і  інваріантні елементи, а інші розташувавши в зростаючому порядку, отримуємо нові множини – додаткові варіаційні ряди:

де – елементи додаткових мінімальних евклідових відстань між ознаками;

    – елементи додаткових максимальних евклідових відстань між ознаками.

Якщо побудовані додаткові варіаційні ряди R_min мають локальні мінімуми, число яких дорівнює , то множина Х складається із  кластерів.

Для додаткових варіаційних рядів R_max число кластерів дорівнює , де  – число локальних мінімумів [3].

Розглянемо встановлення кількості кластерів на прикладі додаткових варіаційних рядів евклідових відстаней R_min і R_max для пари ознак виходу летких речовин V^daf і товщини пластичного шару y. За даними досліджень побудований додатковий варіаційний ряд R_min має один локальний мінімум  і множина Х складається із двох кластерів (). Додатковий варіаційний ряд R_max має один локальний мінімум  і множина Х складається із трьох кластерів ().

Встановлення локальних мінімумів для евклідових відстаней між виходом летких речовин V^daf і середнім показником відбиття вітриніту R_o та між товщиною пластичного шару y і середнім показником відбиття вітриніту R_o на основі аналізу додаткових варіаційних рядів виконується аналогічно. Аналіз додаткових варіаційних рядів евклідових відстаней між класифікаційними показниками марки вугілля по пласту k₅ шахти "Гірник-95" наведено у таблиці 2.

Таблиця 2 – Аналіз додаткових варіаційних рядів

Визначення однорідності структури множини

Для визначення однорідності структури множини Х розрахуємо величину відношення розмаху квадратів ОВР  до розмаху квадратів додаткових варіаційних рядів R_max  за формулою:

Якщо , то множина Х однорідна [3], а якщо – множина Х неоднорідна. Однак ця умова не є достатньою для визначення однорідності множини Х.

Другою характеристикою неоднорідності множини Х обрано  – відношення розмаху квадратів R_min  до розмаху квадратів R_max :

Якщо виконується умова:

то множина Х – однорідна.

При виконаній умові:

то множина Х – неоднорідна.

Розрахунок параметрів однорідності множини Х для даних пласта k₅ шахти "Гірник-95" наведено у таблиці 3.

Аналіз даних, наведених у табл. 3, показав, що множина Х – неоднорідна і запаси вугілля пласта k₅ шахти "Гірник-95" належать до різних марок.

Таблиця 3 – Перевірка однорідності множини

За даними аналізу дослідження поводження основних та додаткових варіаційних рядів  відстаней між різними точками, які є парами ознак класифікаційних показників марок вугілля (виходом летких речовин V^daf і товщиною пластичного шару y; виходом летких речовин V^daf і середнім показником відбиття вітриніту R_o; товщиною пластичного шару y і середнім показником відбиття вітриніту R_o) встановлено, що множина неоднорідна, а значить в ній присутні запаси різних марок. Подальший розподіл запасів вугілля за марками розглянемо на основі застосування методів ієрархічного кластерного аналізу.

Ієрархічний кластерний аналіз

Ієрархічна процедура об'єднання в кластери виконується в такому порядку. Перед початком кластеризації всі об'єкти вважаються окремими кластерами, тобто є p = n кластерів, кожний з яких включає по одному елементу. На першому кроці алгоритму визначаються два найбільш близькі або подібних об'єкти, які поєднуються в один кластер, загальне кількість яких скорочується на 1 (p ® p - 1). Ітеративний процес повторюється, поки на останньому (р - 1)-му кроці всі класи об'єднаються. На кожному наступному кроці процедури об'єднання розраховуються відстані від утвореного кластера до кожного із кластерів, що залишилися.

Ієрархічний кластерний аналіз зручно пояснити методом Ворда. Відмінністю методу Ворда від інших методів є використання методу дисперсійного аналізу для оцінки відстаней між кластерами, у якому мінімізується сума квадратів відстаней для будь-яких двох кластерів, які формуються на кожному кроці. Метод Ворда представляється дуже ефективним, але в ньому створюються кластери малого розміру.

Як дистанційна міра в методі Ворда використається квадрат евклідової дистанції (відстані):

Зведення у квадрат стандартного евклідової відстані виконується для додання більших ваг більше віддаленим один від одного об'єктам.

На рис. 2 представлені дендрограми, на яких графічно показано процес об’єднання в кластери. Початкові 17 об’єктів (показані як номера свердловин) поступово поєднуються спочатку в 3 кластери, а потім в 2 кластери. При цьому розраховуються нові положення центрів кластерів. Ітераційний процес триває доти, поки вони перестають змінювати своє положення.

Рис. 2. Дендрограми класифікації даних методом Ворда

Як видно з рис. 2, на підставі проведеного кластерного аналізу методом Ворда по пласту k₅ шахти "Гірник-95" виділено 2 кластери, що характеризують різний марочний склад вугілля.

Заключним етапом методики геометризації марочного складу вугілля є побудова границь між марками (кластерами). Для цього на план шахтного поля, виконаний в зручному масштабі, наносять границі між кластерами, одержані різними методами (рис. 3). На основі цього обмежується зона, всередині якої розміщені всі криві. З високою ймовірністю можна вважати, що розбіжності результатів об’єкта дослідження знаходяться в одержаної на плані смуги, тобто вона характеризує своєрідний довірчий інтервал границі між двома марками. Візуально намічають середину зони і проводять границю між двома марками вугілля.

Зона характеризує частину площі пласта, в якій розміщується перекриття границь виконаних з використанням розвідувальних даних за різними статистичними методам, в тому числі при застосуванні кластерного аналізу. Графічно по плану оцінюється ширина зони (для пласта k₅ в межах шахти "Гірник-95" вона складає приблизно 1200 м).

За результатами досліджень отримано, що запаси вугілля по пласту k₅ шахти "Гірник-95" для марок К і ПС становлять відповідно 60% і 40%.

Цей розподіл запасів за марками по пласту k₅ шахти "Гірник-95" підтверджуються фактичними даними і документами:

-         даними державного балансу запасів шахти по пласту k₅ шахти "Гірник-95" де вугілля віднесено до марок К і ПС;

-         марка вугілля по балансі виробничих потужностей, затверджених Мінтопенерго України на  08.01.2004 – ПС;

-         результатами фактичного видобутку вугілля шахтою з пласта k₅, відображений у формах 5-ГР, згідно з якою видобуток за марками К і ПС становить відповідно 70%, а ПС - 30%.

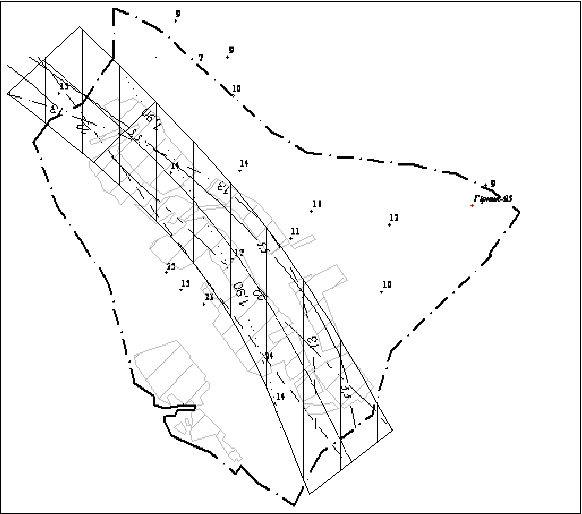
                                                           Масштаб 1:50000 границя по бальній оцінці

                                           Рис. 3. Побудова границь марок по  пласту k₅ шахти "Гірник-95"

Виводи по статті:

1.   Для розподілу запасів вугілля по маркам можна використовувати метод ієрархічного кластерного аналізу.

2.   Проходження границі між марками, яка отримана при застосуванні методу кластерного налізу, підтверджується границями, які отримані при застосуванні інших методів.

3.   Найбільш ймовірними слід вважати зону  і границю, які одержані з використанням різних методів, на основі сукупності різних даних.

4.   Результати, проведених досліджень виявлення границь марочного складу вугілля по пласту k₅ шахти "Гірник-95" надійно підтверджуються фактичними даними видобутку вугілля.

5.   Використовуючи запропоновану методику розмежування запасів вугілля за марками може бути виконане на інших пластах.

Література

1.   Апраушева Н.Н. Три алгоритма естественной кластеризации объектов. – М.: ВЦ АН СССР, 1986. – 22 с.

2.   Апраушева Н.Н. Предварительное обнаружение идеальных кластеров и оценивание их числа. – М.: ВЦ АН СССР, 1987. – 20 с.

3.   Апраушева Н.Н. Некоторые методы обнаружения кластеров. – М.: ВЦ АН СССР, 1988. – 22 с.

4.   Апраушева Н.Н., Ражабов Б.Ж. Экспериментальные исследования по обнаружению кластеров. – М.: ВЦ АН СССР, 1989. – 26 с.

5.   Апраушева Н.Н., Гридина Е.Д. Дополнительные исследования по обнаружению кластеров. – М.: ВЦ АН СССР, 1991. – 20 с.

6.   ДСТУ 3472-96. Вугілля буре, кам’яне та антрацит. Класифікація: Держстандарт України. – Київ, 1997. – 5 с.

7.   Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. – М.: Наука, 1973. – 832 с.

8.   Кремер Н.Ш. Теория вероятности и математическая статистика: Учебник для вузов. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2004. – 573 с.

9.   Могильний С.Г., Кривобоков М.Г. Застосування кластерного аналізу простору ознак при формуванні економіко-планувальних зон // Землевпор. вісн. – 2004. – №4. –  С. 34-40.

10.    Смирнов Н.В., Белугин Д.А. Теория вероятностей и математическая статистика в приложении к геодезии. – М.: Недра, 1969. – 379 с.