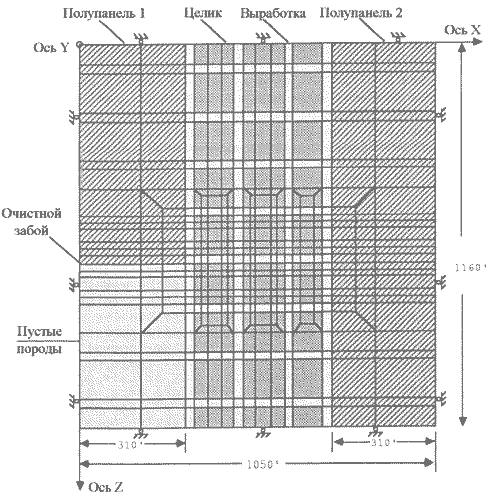
Рисунок 1 – Обзорный план модели и сетки конечных элементов.
Источник: Park, D. W. and Gall, V. (1989) Supercomputer assisted three-dimensional finite element analysis of a longwall panel. Rock Mechanics as a Guide for Efficient Utilization of Natural Resources, Proc. 30th U. S. Rock Mech. Symp., Morgantown (ed. A. W. Khair), 133-40. A. A. Balkema: Rotterdam.
Отработка длинных очистных забоев порождает постоянное перераспределение напряжений в окружающем массиве горных пород при каждом подвигании очистного забоя. Понимание поведения пород, которые подвержены высокому уровню напряженного состояния, является инструментом для того, чтобы правильно выбирать параметры подземной разработки шахт. Чтобы сделать реалистичный анализ поведения таких массивов часто используют метод конечных элементов, причем в трехмерной его постановке. Эта модель также разработана для того, чтобы анализировать большую репрезентативную часть массива, который подвержен влиянию очистного забоя; для этого необходимо было разбить на достаточное количество элементов, чтобы получить детальную информацию распределения напряжений и смещений. Ввиду большого размера модели решение этой задачи было получено с помощью суперкомпьютера CRAY X-MP/24.
Участок, выбранный для анализа, расположен на поле шахты «Черных воинов» в Алабаме. Шахта имеет два выемочных участка в виде длинных очистных забоев на глубине 2000 футов с различными размерами «цепных» охранных целиков, включая и податливые целики. Разнообразные исследовательские программы на этой шахте были выполнены Парком [4]. Были собраны данные по геологии, физическим свойствам массива горных пород и угля. Кроме того, была проведена программа по дополнительному испытанию пород, чтобы получить классификацию этих пород.
Для моделирования постоянного перераспределения напряжения была использована процедура прогрессирующих разрушений. Использовался критерий разрушения Хоека и Брауна [1], который базируется на поведении горного массива и процесс моделирования разрушения осуществлялся с помощью итерационной процедуры. Благодаря этому моделирование сдвижений было весьма реалистично. Для того чтобы автоматизировать процесс расчета прогрессирующих разрушений была разработана специальная компьютерная программа. В итоге была скомбинирована крупномасштабная трехмерная модель с помощью конечных элементов и автоматизирована процедура прогрессирующего разрушения; модель стала инструментом, порождающим огромное количество информации, которая описывает поведение массива горных пород и угля как отклик на отработки длинных очистных забоев.
Трехмерная конечно-элементная модель представляет собой участок 1060х1050 футов, который состоит из трех рядов целиков и двух половин длинных очистных забоев. Половина панели имеет длину 310 футов и расположена по обе стороны относительно системы цепных целиков (см. рис. 1). Общая высота модели составляет более 2000 футов и включает в себя 2 слоя, расположенных ниже угольного пласта. Модель в вертикальном направлении имеет 14 стратиграфических слоев. Это дает практическое представление о стратиграфической последовательности над шахтой. Каждый слой состоит из 531 восьмиузлового гексаэдрального элемента. В итоге общее число элементов – 7434. В области забоя сетка конечных элементов была усовершенствована для возможности детального анализа напряжений в целиках и плоскости очистного забоя. Граничные условия для модели были наложены с единственными ограничениями в направлении оси Х для двух вертикальных границ плоскости Y-Z и в направлении оси Z для двух вертикальных границ плоскости Y-Х. Верхняя граница плоскости Х-Z закреплена в направлении оси Y.

Данные о материалах, такие как модуль упругости, коэффициент Пуансона, удельный вес и прочность были получены в предыдущих изучениях, осуществленных Парком [3] и выполнялась программа по изучению пород. Она была связана с изучением параметров классификации горных пород.
В этом изучении смоделировано отступление системы очистных выработок. Пустое пространство в зоне пустых пород играет важную роль в изучении повышенного давления, если фрагменты отбитой породы компактны. Сложно оценить протяженность зоны пустых пород, потому что неизвестна последовательность процесса разрушения в непосредственной и основной кровле. Модель пустых пород в данной работе основана на моделировании Пенга [6]. Были использованы различные значения модуля упругости для моделирования пустых пород от 2500 до 20000 Psi в зависимости от расположения для определения роста сжатия в направлении от плоскости забоя. Эти значения находятся в диапазоне от 1000 до 47000 Psi, полученные Пенгом [5]. Коэффициент Пуансона равный 0,45 был использован для всех материалов пустых пород.
Гексаэдральными элементами была попытка смоделировать усиленную поддержку. Модуль упругости составил 1080 Psi и коэффициент Пуансона 0,3 были назначены ряду элементов, находящихся в углах очистного забоя. Напряжения в этих элементах в начальном состоянии были вычислены путем нагрузки пустыми породами. Получена нагрузка в диапазоне 600 тонн.
Конечно-элементное моделирование было выполнено на CRAY X-MP/24, ядре суперкомпьютерной сети Алабамы.
Использован конечно-элементный код программного пакета ANSYS 4.3. Сетка конечных элементов была создана с помощью модуля сетей включенного в пакет. Как только была сгенерирована сеть конечных элементов, она сохранена в отдельный ANSYS файл. Для каждого последующего расчета, выполненного моделированием прогрессирующего разрушения, должен быть подготовлен только входной файл, содержащий измененные свойства материалов.
Явление прогрессирующего разрушения пород и угля было смоделировано с использованием способа повторений, который уже показал большой успех в двумерном моделировании Парка [4,3]. Способ требует модификации свойств материала и основана на напряженном состоянии отдельного элемента.
В данной работе используется норма конвергенции в факторах снижения как критерий для окончания моделирования прогрессирующих разрушений. Углы целиков, касающиеся забоя, в начальном состоянии показывают наибольшие напряжения (см. рис. 2) и поэтому перераспределение напряжения будет иметь место в самой большой норме в этом расположении. Благодаря этому конвергенция факторов снижения критическая, особенно в этом участке. После ряда повторений высокие давления со стороны забоя и в углах целиков будут перенесены в центры целиков [2]. Между явлением перераспределения напряжений и сближением фактором снижения была найдена корреляция.

Результаты, представленные в этой статье, учитывают перераспределение напряжений в секции, где сетка конечных элементов была усовершенствована, как показано на рис. 1. После пятой итерации в элементах целиков получена норма конвергенции менее чем 1%. Это дало высокие напряжения в углах целиков, опирающихся на очистной забой в начальном решении, и повторение было закончено. Распределение напряжения показано на рис. 2-4. Напряжения в углах целиков значительно уменьшены, особенно в целиках рядом с пустыми породами. Напряжения переносятся с углов целиков в их центры. Опорное давление в очистном забое также уменьшено пока было уменьшено опорное давление неотработанной части панели. Полное перераспределение напряжений расположено вдали от зоны очистного забоя и пустых пород в направлении неотработанных секций очистной панели. Это представляет очень реалистическое моделирование фактического распределения напряжений в шахте.
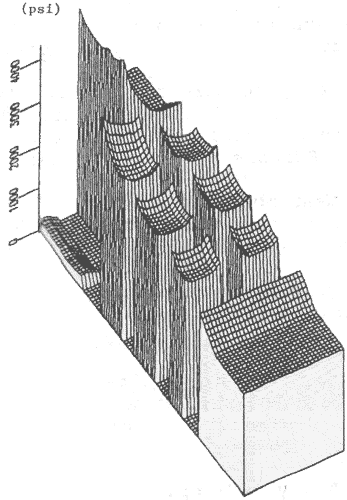
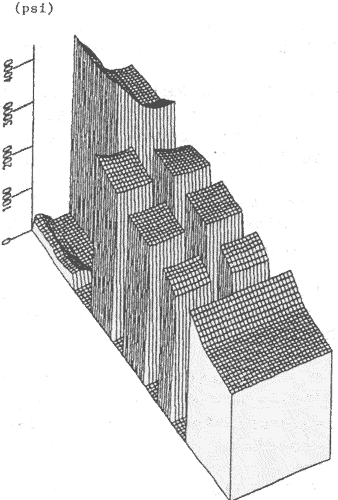
Критерий разрушений Брауна и Хоека, рассматривающий свойство массива горных пород, примененный в трехмерном конечно-элементном моделировании очистной панели показал хорошие результаты. Пригодность суперкомпьютера предоставляет возможность осуществлять моделирование большого масштаба. Автоматизированная процедура для прогрессирующего разрушения обеспечивает легкую обработку данных. Комбинация трехмерной модели с техникой моделирования прогрессирующего разрушения дает возможность реалистичного моделирования работ в очистной панели. Крупномасштабная трехмерная конечно-элементная модель также детально изучает не только участки вблизи забоя, как представлено в этой работе, но и также давление арки, поверхности и под поверхностью падения.