История изучения нестационарных гидродинамических процессов, включающих в частности гидравлический удар, насчитывает уже более ста лет и начинается со ставшей в настоящее время уже классической работы Н.Е. Жуковского [1].
В прошедшие годы явление гидравлического удара неизменно привлекало внимание ученых и инженеров во многих странах в связи с научным и практическим аспектами. К началу шестидесятых годов прошлого столетия основные физические и гидродинамические процессы, протекающие в элементах трубопроводных систем при гидравлическом ударе, были в основном изучены. В то же время было установлено, что в реальных (сложных) гидросистемах специфика переходных процессов в основном определяется многократным наложением отраженных от конструктивных неоднородностей системы волн давления и трансформацией этих волн при их прохождении по длине трубопроводов. В сложных гидросистемах, как и во многих других инженерных задачах, решению препятствует «проклятие многомерности», усугубляемое нелинейностью процессов.
На переходные процессы оказывают влияние большое количество факторов, например, наличие в трубах растворенного в жидкости воздуха, деформационная податливость стенок труб и другие явления. В частности, было установлено, что на характер нестационарных процессов в трубопроводных системах кардинальное влияние оказывают кавитационные разрывы сплошности, которые могут возникать в любой точке системы при падении давления там ниже величины давления насыщенных паров жидкости. Поэтому не удивительно, что в конце шестидесятых годов прошлого века система, состоящая из двух труб разного диаметра, считалась у специалистов «сложной»и трудно поддающейся расчету.
Важным вкладом в методику расчета гидравлического удара было создание «графического» метода, изложенного лучше всего в монографии Л. Бержерона [2]. Однако, даже специалистами в области гидравлического удара, расчеты могли выполняться лишь для достаточно простых гидросистем, состоящих из одной, двух труб, и без учета нелинейных и кавитационных процессов. Все это не позволяло гарантировать достаточную, даже для инженерных систем, точность расчета и возможность массового использования метода в повседневной практике.
Очередной (решающий) шаг в расчетах гидравлического удара - отказ от аналитических и графических методов в пользу численных, позволило сделать начало массового использования электронно-вычислительных машин. Их внедрение и массовое использование позволило проводить расчеты практически без ограничения сложности сетей.
Определенный итог выполненных в этом направлении работ и исследований был подведен в монографиях В.Л. Стритера и Е.Б. Уайли [3] (США), Б.Ф. Лямаева, Г.П. Небольсина и В.А. Нелюбова [4] (СССР), опубликованных в шестидесятых - семидесятых годах двадцатого века. В этих работах приведены методы и результаты решения основных проблем при создании компьютерных моделей для проведения численного эксперимента по изучению нестационарных процессов в реальных (сложных) трубопроводных системах на ЭВМ. Это позволило существенно повысить точность и достоверность расчетов, в том числе за счет привлечения более точных нелинейных моделей для описания распространения волн в трубах и поведения конструктивных элементов системы, учета кавитационных явлений.
Современным подходом при разработке программ для расчета режимов работы инженерных сетей, в частности и для расчета нестационарных гидродинамических процессов в трубопроводных системах, является создание программно-расчетных комплексов для компьютеров на основе использования геоинформационных технологий (ГИС). Это позволяет решать весь перечень задач, связанных с разработкой, проектированием и эксплуатацией гидросистем различного назначения для конкретных условий.
Применение геоинформационных технологий для создания моделей водопроводных сетей и, в частности, исследования нестационарных процессов дает существенное преимущество по сравнению с использованием других программных продуктов, не имеющих в своей основе геоинформационной системы. Это преимущество определяется следующим:
Возможностью использования графической подосновы (карты города, района, населенного пункта) для нанесения на нее водопроводной сети.
Простотой нанесения на карту города схемы водопроводной сети с ее привязкой к существующим зданиям и сооружениям, наглядностью представления информации, быстрым вводом исходных данных, необходимых для выполнения расчетов и удобством анализа полученных результатов расчета.
Процесс нанесение водопроводной сети на карту города максимально автоматизирован. Для этого достаточно при помощи мыши в графическом редакторе изобразить схему водопроводной сети. При этом автоматически создается топологически связный граф сети с привязкой соответствующих баз данных к каждому объекту.
В последнее время в связи с частыми отключеньями электроэнергии участились случаи возникновения гидроударов, поэтому более острой становится потребность в защите от гидроудара. При выборе защитных устройств существенную помощь может оказать компьютерная программа, позволяющая сразу оценить эффективность планируемых мероприятий.
Компания «Политерм», имеющая богатый опыт в разработке программного обеспечения для гидравлических и тепловых стационарных расчетов, предлагает новый программный продукт, предназначенный для расчета переходных процессов (в том числе и при возникновении гидравлического удара) в трубопроводных системах. Программный продукт создан с использованием опыта, накопленного научными школами одного из старейших вузов России Военного инженерно-технического университета. Программа, выполняющая расчеты гидравлического удара, оформлена в виде модуля расширения (plug-in) геоинформационной системы Zulu и входит в программно-расчетный комплекс ZuluHydro.
Кратко опишем возможности программы и используемую математическую модель. Известно, что переходные процессы в водопроводных сетях возникают чаще всего при включении и выключении насосов, а также при открытии и закрытии задвижек. Гидравлический удар является следствием быстрого выполнения одного или нескольких перечисленных действий и может усугубляться наличием воздушных полостей в трубах. В программе предусмотрена возможность выбора пользователем источника возмущения стационарного процесса. В процессе расчета и по его завершению пользователю для анализа переходных процессов программа предоставляет следующую информацию:
В процессе расчета пользователь имеет возможность наблюдать в реальном времени распространение бегущих волн давления и скорости вдоль любого маршрута.
По результатам расчета производится построение графиков наибольшего и наименьшего давлений в каждой точке вдоль этого маршрута.
Приводятся графики изменения давления в зависимости от времени для ряда выбранных точек наблюдения.
В базы данных заносятся значения наибольшего и наименьшего давлений для каждого участка и узла сети с указанием времени возникновения этих давлений, а для участка указываются и соответствующие точки.
ГИС Zulu позволяет с помощью запросов найти по базе данных наиболее опасные участки и узлы и на основании этой информации можно при необходимости выбрать (или добавить) другие точки наблюдения и изменить маршрут для построения графиков.
Отметим, что наряду с зонами повышенного давления определенную опасность представляют и зоны пониженного давления. В этом случае возможен подсос загрязненных грунтовых вод в систему водоснабжения, что может привести к возникновению эпидемий, кроме того, могут проявляться эффекты, связанные с кавитацией.
Остановимся подробнее на основных моментах описания математической модели, использованной при разработке программы расчета гидравлического удара.
Трубопроводная сеть (с математической точки зрения - взвешенный ориентированный граф) состоит из участков (труб) и узлов (соединение труб, потребитель, воздушный колпак, резервуар и так далее). С математической точки зрения насос и задвижка представляют собой участки, хотя на схеме они изображаются узлами. Пользователю о таких вещах беспокоиться не приходится - кодировка сети выполняется программой автоматически.
Распространение волн сжатия и разрежения в трубах описывается квазилинейной системой дифференциальных уравнений первого порядка с частными производными
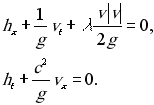 Здесь
Здесь 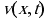 - скорость, а
- скорость, а  - пьезометрический напор, нижний индекс означает частную производную по соответствующей переменной. Решение этой системы проводится численным методом характеристик:
- пьезометрический напор, нижний индекс означает частную производную по соответствующей переменной. Решение этой системы проводится численным методом характеристик:
 Здесь использованы, как и в монографии [5] следующие обозначения: нижний индекс R или S означает, что соответствующая физическая величина берется в предыдущем слое по времени либо в точке слева, либо справа от расчетной точки с индексом P, c - скорость звука, g - ускорение свободного падения, d - диаметр трубы, f - коэффициент гидравлического сопротивления.
Здесь использованы, как и в монографии [5] следующие обозначения: нижний индекс R или S означает, что соответствующая физическая величина берется в предыдущем слое по времени либо в точке слева, либо справа от расчетной точки с индексом P, c - скорость звука, g - ускорение свободного падения, d - диаметр трубы, f - коэффициент гидравлического сопротивления.
Заметим, что скорость распространения волн ввиду наличия растворенного воздуха существенным образом зависит от давления. Учитывается так же влияние на скорость упругости стенок трубы [5]
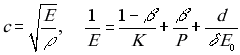 Здесь
Здесь  - доля (объемная) нерастворенного воздуха в воде,
- доля (объемная) нерастворенного воздуха в воде, .gif) - плотность смеси вода-воздух, E - модуль Юнга для смеси вода-воздух с поправкой на упругость трубы, K - модуль упругости воды при отсутствии нерастворенного воздуха, d - диаметр трубы,
- плотность смеси вода-воздух, E - модуль Юнга для смеси вода-воздух с поправкой на упругость трубы, K - модуль упругости воды при отсутствии нерастворенного воздуха, d - диаметр трубы,  - толщина стенки трубы, - модуль Юнга материала трубы.
- толщина стенки трубы, - модуль Юнга материала трубы.
Уравнения следует решать при начальных условиях, получаемых с помощью стационарного гидравлического расчета (мы используем расчетный модуль ZuluHydro), и граничных условиях, определяемых конструктивными элементами. Например: потребитель с заданным расходом описывается граничным условием вида , а резервуар (при достаточно большой поверхности) условием
, а резервуар (при достаточно большой поверхности) условием 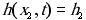 .
.
К более сложным граничным условиям приводят: соединение нескольких труб в одном узле, воздушный колпак, насос, задвижка, локальное сопротивление, разрушаемая мембрана, потребитель с заданным гидравлическим сопротивлением.
Наличие задвижки приводит к граничным условиям
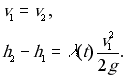 Здесь
Здесь 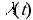 - безразмерный коэффициент сопротивления задвижки. Для каждого конкретного типа задвижки коэффициент сопротивления можно выразить через степень закрытия задвижки, а зависимость последнего от времени задает пользователь, например, можно задать время начала закрытия, продолжительность процесса и назначить линейную зависимость степени закрытия от времени.
- безразмерный коэффициент сопротивления задвижки. Для каждого конкретного типа задвижки коэффициент сопротивления можно выразить через степень закрытия задвижки, а зависимость последнего от времени задает пользователь, например, можно задать время начала закрытия, продолжительность процесса и назначить линейную зависимость степени закрытия от времени.
Взаимодействие насоса с потоком жидкости описывается уравнением движения
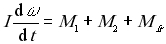 где I - момент инерции насосного агрегата,
где I - момент инерции насосного агрегата,  - угловая скорость вращения рабочего колеса насоса,
- угловая скорость вращения рабочего колеса насоса,  - вращающий момент электродвигателя,
- вращающий момент электродвигателя,  - момент с которым жидкость воздействует на рабочее колесо насоса,
- момент с которым жидкость воздействует на рабочее колесо насоса, 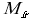 - момент сил трения.
- момент сил трения.
Простейшая модель насоса описывается следующим образом. Задается G-H характеристика насоса в виде параболы
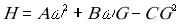 Тогда граничные условия примут вид
Тогда граничные условия примут вид
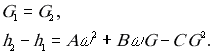 Расход G очевидным образом выражается через скорость
Расход G очевидным образом выражается через скорость 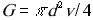 .
.
При наличии обратного клапана в случае возникновении отрицательного расхода жидкости через насос, срабатывание обратного клапана приводит к граничному условию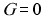 .
.
Отметим, что в программе имеются справочники по задвижкам и насосам, что позволяет пользователю либо выбрать устройство из справочника либо добавить в список новое устройство и ввести характеристику табличным способом.
Воздушный колпак описывается следующими граничными условиями
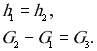 Здесь
Здесь 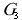 - расход жидкости, втекающей в воздушный колпак, и он зависит от разности давлений (и соответственно напоров) жидкости в месте соединения колпака с трубой и воздуха внутри колпака
- расход жидкости, втекающей в воздушный колпак, и он зависит от разности давлений (и соответственно напоров) жидкости в месте соединения колпака с трубой и воздуха внутри колпака
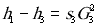 Давление воздуха внутри колпака находится из уравнения состояния газа (изотерма, адиабата или политропа)
Давление воздуха внутри колпака находится из уравнения состояния газа (изотерма, адиабата или политропа)
 Здесь
Здесь  и
и  - давление и объем воздуха в начальный момент времени.
- давление и объем воздуха в начальный момент времени.
Наконец, для отыскания объема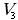 имеем уравнение
имеем уравнение
 ,
,
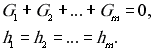 Таким образом, в одном программном комплексе можно проводить расчеты, как стационарных режимов, так и нестационарных для любых по сложности систем водоснабжения.
Таким образом, в одном программном комплексе можно проводить расчеты, как стационарных режимов, так и нестационарных для любых по сложности систем водоснабжения.
Приведем пример расчета переходных процессов для простейшей сети, состоящей из резервуара, колодца, задвижки и потребителя.
На рисунках 1 и 2 показаны окно управления расчетами и окно результатов расчета.
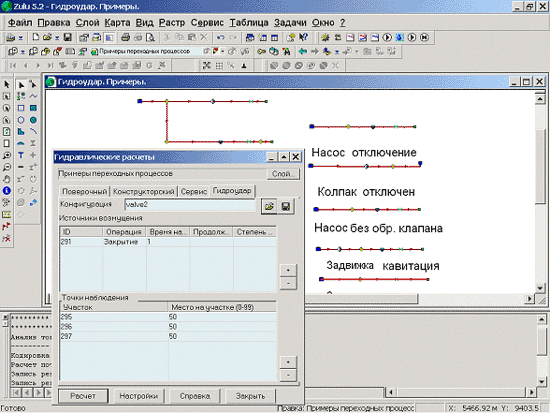
Рис. 1
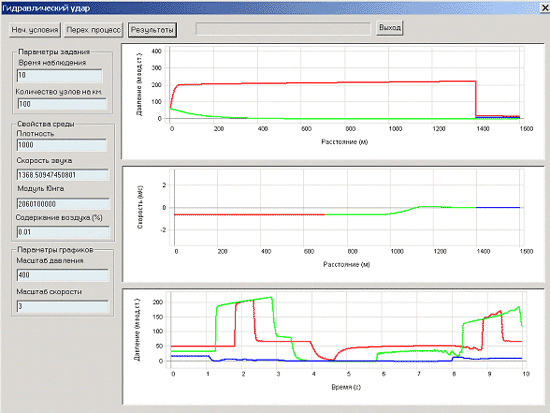
Рис. 2
На верхнем графике наибольшее и наименьшее давление в каждой точке вдоль трубы за все время численного эксперимента.
На среднем графике остановлена бегущая волна в последний момент расчета.
На нижнем графике показано изменение давления в зависимости от времени в трех выбранных точках наблюдения.
Вывод: Организацией «Политерм» создан современный программный комплекс для расчета стационарных и переходных процессов в трубопроводных системах любой сложности.
Литература
Жуковский Н.Е. О гидравлическом ударе в водопроводных трубах. М.-Л., Гостехиздат, 1949. 103 с.
Бержерон Л. От гидравлического удара в трубах до разряда в электрической сети. Общий графический метод расчета. (Перевод с франц.) М., Машгиз, 1962. 348 с.
Streeter V.L., Wylie E.B. Hydraulic Transients. New York, Mc Craw - Hill, 1967. 317 p.
Лямаев Б.Ф., Небольсин Г.П., Нелюбов В.А. Стационарные и переходные процессы в сложных гидросистемах. Методы расчета на ЭВМ. Под ред. Б.Ф. Лямаева.- Л., Машиностроение. Ленинградское отделение, 1978. - 192 с.
Фокс Д.А. Гидравлический анализ неустановившегося течения в трубопроводах. М, 1981.
На переходные процессы оказывают влияние большое количество факторов, например, наличие в трубах растворенного в жидкости воздуха, деформационная податливость стенок труб и другие явления. В частности, было установлено, что на характер нестационарных процессов в трубопроводных системах кардинальное влияние оказывают кавитационные разрывы сплошности, которые могут возникать в любой точке системы при падении давления там ниже величины давления насыщенных паров жидкости. Поэтому не удивительно, что в конце шестидесятых годов прошлого века система, состоящая из двух труб разного диаметра, считалась у специалистов «сложной»и трудно поддающейся расчету.
Важным вкладом в методику расчета гидравлического удара было создание «графического» метода, изложенного лучше всего в монографии Л. Бержерона [2]. Однако, даже специалистами в области гидравлического удара, расчеты могли выполняться лишь для достаточно простых гидросистем, состоящих из одной, двух труб, и без учета нелинейных и кавитационных процессов. Все это не позволяло гарантировать достаточную, даже для инженерных систем, точность расчета и возможность массового использования метода в повседневной практике.
Очередной (решающий) шаг в расчетах гидравлического удара - отказ от аналитических и графических методов в пользу численных, позволило сделать начало массового использования электронно-вычислительных машин. Их внедрение и массовое использование позволило проводить расчеты практически без ограничения сложности сетей.
Определенный итог выполненных в этом направлении работ и исследований был подведен в монографиях В.Л. Стритера и Е.Б. Уайли [3] (США), Б.Ф. Лямаева, Г.П. Небольсина и В.А. Нелюбова [4] (СССР), опубликованных в шестидесятых - семидесятых годах двадцатого века. В этих работах приведены методы и результаты решения основных проблем при создании компьютерных моделей для проведения численного эксперимента по изучению нестационарных процессов в реальных (сложных) трубопроводных системах на ЭВМ. Это позволило существенно повысить точность и достоверность расчетов, в том числе за счет привлечения более точных нелинейных моделей для описания распространения волн в трубах и поведения конструктивных элементов системы, учета кавитационных явлений.
Современным подходом при разработке программ для расчета режимов работы инженерных сетей, в частности и для расчета нестационарных гидродинамических процессов в трубопроводных системах, является создание программно-расчетных комплексов для компьютеров на основе использования геоинформационных технологий (ГИС). Это позволяет решать весь перечень задач, связанных с разработкой, проектированием и эксплуатацией гидросистем различного назначения для конкретных условий.
Применение геоинформационных технологий для создания моделей водопроводных сетей и, в частности, исследования нестационарных процессов дает существенное преимущество по сравнению с использованием других программных продуктов, не имеющих в своей основе геоинформационной системы. Это преимущество определяется следующим:
Возможностью использования графической подосновы (карты города, района, населенного пункта) для нанесения на нее водопроводной сети.
Простотой нанесения на карту города схемы водопроводной сети с ее привязкой к существующим зданиям и сооружениям, наглядностью представления информации, быстрым вводом исходных данных, необходимых для выполнения расчетов и удобством анализа полученных результатов расчета.
Процесс нанесение водопроводной сети на карту города максимально автоматизирован. Для этого достаточно при помощи мыши в графическом редакторе изобразить схему водопроводной сети. При этом автоматически создается топологически связный граф сети с привязкой соответствующих баз данных к каждому объекту.
В последнее время в связи с частыми отключеньями электроэнергии участились случаи возникновения гидроударов, поэтому более острой становится потребность в защите от гидроудара. При выборе защитных устройств существенную помощь может оказать компьютерная программа, позволяющая сразу оценить эффективность планируемых мероприятий.
Компания «Политерм», имеющая богатый опыт в разработке программного обеспечения для гидравлических и тепловых стационарных расчетов, предлагает новый программный продукт, предназначенный для расчета переходных процессов (в том числе и при возникновении гидравлического удара) в трубопроводных системах. Программный продукт создан с использованием опыта, накопленного научными школами одного из старейших вузов России Военного инженерно-технического университета. Программа, выполняющая расчеты гидравлического удара, оформлена в виде модуля расширения (plug-in) геоинформационной системы Zulu и входит в программно-расчетный комплекс ZuluHydro.
Кратко опишем возможности программы и используемую математическую модель. Известно, что переходные процессы в водопроводных сетях возникают чаще всего при включении и выключении насосов, а также при открытии и закрытии задвижек. Гидравлический удар является следствием быстрого выполнения одного или нескольких перечисленных действий и может усугубляться наличием воздушных полостей в трубах. В программе предусмотрена возможность выбора пользователем источника возмущения стационарного процесса. В процессе расчета и по его завершению пользователю для анализа переходных процессов программа предоставляет следующую информацию:
В процессе расчета пользователь имеет возможность наблюдать в реальном времени распространение бегущих волн давления и скорости вдоль любого маршрута.
По результатам расчета производится построение графиков наибольшего и наименьшего давлений в каждой точке вдоль этого маршрута.
Приводятся графики изменения давления в зависимости от времени для ряда выбранных точек наблюдения.
В базы данных заносятся значения наибольшего и наименьшего давлений для каждого участка и узла сети с указанием времени возникновения этих давлений, а для участка указываются и соответствующие точки.
ГИС Zulu позволяет с помощью запросов найти по базе данных наиболее опасные участки и узлы и на основании этой информации можно при необходимости выбрать (или добавить) другие точки наблюдения и изменить маршрут для построения графиков.
Отметим, что наряду с зонами повышенного давления определенную опасность представляют и зоны пониженного давления. В этом случае возможен подсос загрязненных грунтовых вод в систему водоснабжения, что может привести к возникновению эпидемий, кроме того, могут проявляться эффекты, связанные с кавитацией.
Остановимся подробнее на основных моментах описания математической модели, использованной при разработке программы расчета гидравлического удара.
Трубопроводная сеть (с математической точки зрения - взвешенный ориентированный граф) состоит из участков (труб) и узлов (соединение труб, потребитель, воздушный колпак, резервуар и так далее). С математической точки зрения насос и задвижка представляют собой участки, хотя на схеме они изображаются узлами. Пользователю о таких вещах беспокоиться не приходится - кодировка сети выполняется программой автоматически.
Распространение волн сжатия и разрежения в трубах описывается квазилинейной системой дифференциальных уравнений первого порядка с частными производными
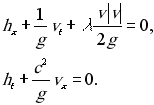

Заметим, что скорость распространения волн ввиду наличия растворенного воздуха существенным образом зависит от давления. Учитывается так же влияние на скорость упругости стенок трубы [5]
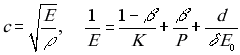
Уравнения следует решать при начальных условиях, получаемых с помощью стационарного гидравлического расчета (мы используем расчетный модуль ZuluHydro), и граничных условиях, определяемых конструктивными элементами. Например: потребитель с заданным расходом описывается граничным условием вида
К более сложным граничным условиям приводят: соединение нескольких труб в одном узле, воздушный колпак, насос, задвижка, локальное сопротивление, разрушаемая мембрана, потребитель с заданным гидравлическим сопротивлением.
Наличие задвижки приводит к граничным условиям
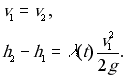
Взаимодействие насоса с потоком жидкости описывается уравнением движения
Простейшая модель насоса описывается следующим образом. Задается G-H характеристика насоса в виде параболы
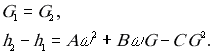
При наличии обратного клапана в случае возникновении отрицательного расхода жидкости через насос, срабатывание обратного клапана приводит к граничному условию
Отметим, что в программе имеются справочники по задвижкам и насосам, что позволяет пользователю либо выбрать устройство из справочника либо добавить в список новое устройство и ввести характеристику табличным способом.
Воздушный колпак описывается следующими граничными условиями
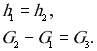

Наконец, для отыскания объема
которое приходится решать численно, поскольку зависимость 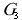 от времени не известна.
от времени не известна.
Сложное соединение труб (соединение нескольких труб в одном узле) приводит к граничным условиям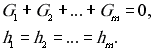
Приведем пример расчета переходных процессов для простейшей сети, состоящей из резервуара, колодца, задвижки и потребителя.
На рисунках 1 и 2 показаны окно управления расчетами и окно результатов расчета.

Рис. 1

Рис. 2
На среднем графике остановлена бегущая волна в последний момент расчета.
На нижнем графике показано изменение давления в зависимости от времени в трех выбранных точках наблюдения.
Вывод: Организацией «Политерм» создан современный программный комплекс для расчета стационарных и переходных процессов в трубопроводных системах любой сложности.
Литература