TAC Menta

 

Process models description

 

1.  Introduction

Within the TAC Menta environment a number of models of common HVAC processes, such as heating coils, cooling coils, fans etc. have been developed. The models can be used together with an application program. By connecting the application program to suitable models, we are able to simulate not only the application program, but also how the control system and the physical processes will influence each other (system behaviour). In this way we can get good knowledge about the system behaviour already in the programming phase.

But the most important reason for using the process models are probably not that they provide us with general information about the system. The system simulation also gives us an excellent tool for trouble-shooting in a very convenient and efficient environment. Once you get used to working with the process models, you will probably notice that a number of programming errors that before usually were discovered during commissioning, now are detected during the programming phase.

1.1.  Model accuracy and restrictions

When you make models of physical processes it is important to know how the models are going to be used.

If you e.g. are a heat exchanger manufacturer, you might be interested in making a heat exchanger model for accurate calculation of the heat transfer for different water velocities and plate properties. This approach would probably lead to a complex model. Also note that the heat exchanger manufacturer may not be so interested in the dynamic behaviour if he is primarily interested in calculating the heat exchanger efficiency.

An application programmer or someone working with commissioning has completely different demands on the model. They are interested in models that can be used for evaluating the control system. The models must describe the dynamic behaviour but the demands on accuracy are moderate. The models should preferably be relatively simple because simple models take less screen space and will execute faster. The purpose of the models in this library is primarily to fulfil the demands for this later category of people.

Since the models in this library are quite simple they naturally have some restrictions.

An important restriction for the component models used in ducts, i.e. Cooler, Dehumidifier, Heater, Heater humidity, Humidifier, Humidifier complex and HX Air2Air is that they are designed under the assumption that we have a constant air flow in the duct. In these models the air flow is set as a constant or in some cases (Cooler and HX Air2Air) we have not taken the air flow dependence into consideration at all. This implies that we can not use the models in this library for studying what happens with the temperature and the humidity when we have a varying air flow. A special case of this is when fans are started and stopped. Note that the Fan speed model of course work with varying flow, but the behaviour of the other components are not affected by the air flow calculated in this model. This is of course not a physically correct behaviour but we designed the models in this way to keep them simple.

1.2.  To use process models; a simple AHU example

We will here give an example of how the process models are supposed to be used. The application is supply temperature control in a simple AHU consisting of a heating coil, a heat recovering rotating wheel and a cooling coil, see Figure 1.1. For simplicity we will disregard the control of the fans.

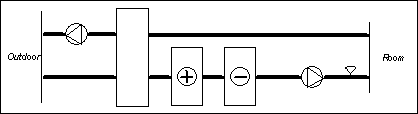
Figure 1.1. Simple air handling unit.

In this example we have chosen to have different cooling and heating setpoints. The controller switches to heating operation when the supply temperature is below the heating setpoint and it switches to cooling operation when the supply temperature is above the cooling setpoint. Since we want to keep the example relatively simple we are just studying the sequence in normal operation, i.e. we have no freeze protection, cool recovery etc. The question is now, how do we use the process models to check that our supply temperature control program works as desired.

The first step is to define what the HVAC system looks like, i.e. what components the system consists of and how they are connected. In our example we have 3 components that influence the supply temperature (we neglect the influence of the supply fan on the supply temperature), the rotating wheel, the heating coil and the cooling coil. This implies that we will need the following models from the model library; HX Air2Air (model of a rotating wheel), Heater (model of a heating coil) and Cooler (model of a cooling coil).

The next step is to decide how the inputs of a certain model should be connected. To be able to do that, it is often helpful to have a schematic picture of the HVAC system like in Figure 1.1. A TAC Menta program for the application is shown in the file Model demo.aut which can be consulted while reading this section.

Let us see how the model of the rotating wheel (HX Air2Air) should be connected. This model has 3 inputs. The inputs are; Temperature before HEX (supply), Temperature before HEX (return) and Control signal. If we take a look at Figure 1.1 we see that the supply air to the HEX comes directly from outdoor, i.e. we should connect an outdoor temperature to the input Temperature before HEX (supply). We could e.g. use a PVR block with the value 10 to represent the outdoor temperature. In the same way we see that the return air entering the HEX is coming from the room. If we assume that the room temperature is 25 °C, we can connect a PVR block with the value 25 to the input Temperature before HEX (return). Finally, we have to connect the Control Signal. This signal is an output from the controller. The connection of the Control Signal is a bit different compared to the other input signals, since it should be connected to a physical output of the controller. Signals that come from physical outputs should be connected to the models via a test probe, see the Reference Manual. In the reversed case where we have signals from the model that are used in the control program, these signals are also connected to test probes, see SupplyTemp in Model demo.aut. The control program can then read these signals via their physical inputs.

In some cases it may be necessary to adjust the constants. The general rule is however that if you are not an experienced user you should stick to the nominal values. The reason for this is that the models have been tested with these constants and proved to give good results.

2.  Process models

2.1.  Model summary

                                Cooler     Simple model of cooling coil. Only temperature relations taken into consideration.

                      Dehumidifier     Model of cooling coil. Temperature and humidity relations taken into consideration.

                          Fan speed     Model of speed controlled fan.

                                Heater     Model of a heating coil.

                 Heater humidity     Model of a heating coil. The temperature relations are the same as in Heater but Heater humidity in addition to the temperature also computes the relative humidity.

                         Humidifier     Simple model of a humidifier that injects steam into an air stream. Only accurate within a limited temperature range.

           Humidifier complex     Model of a humidifier that injects steam into an air stream. The stationary relations are accurate within a wide range of operating conditions.

                        HX Air2Air     Model of an air-to-air heat exchanger (rotating wheel).

               HX Water2Water     Model of a water-to-water heat exchanger (plate type).

                                  Room     Simple model of the temperature dynamics of a room. The room temperature is controlled by changing the supply air temperature.

                   Room complex     Model of the temperature dynamics of a room. The room temperature is controlled by changing the supply air temperature. The dynamics of the room is calculated from physical data of the room.

2.2.  How to use a certain model

In this section we give some more details about the different models. We also give some hints on how to use the model.

2.2.1.  Cooling coil (Cooler)

Description

Cooler is a simple model of a cooling coil. The dynamics of the air is modelled as a first order filter with nominal time constant = 30 s. The air temperature fall (°C) in steady-state when 100% of the cooling capacity is used is defined by the PVR block MaxFall. The nominal value of MaxFall is 20 °C.

Hints

By increasing the value of MaxFall, a higher cooling capacity is achieved. Tai is typically connected to the outdoor temperature or the output of a model situated in front of the cooler in the duct. If Tai is connected to the outdoor temperature, the response from the tempera­ture control loop can be checked by changing (a disturbance) Tai.

Inputs

Tai = incoming air temperature (°C). Real.

uc = control signal (0–100%). Real.

Outputs

Tao = outgoing air temperature (°C). Real.

2.2.2.  Dehumidification with a cooling coil (Dehumidifier)

Description

Dehumidifier is a model of dehumidification with a cooling coil. Since this process is quite complicated we have to make some assumptions in order to get a reasonably simple model.

We consider the cooling coil to consist of three parts, the coolant inside the pipes (together with the metal of the coil), an air film on the coil surfaces and the air stream. The state of the air leaving the coil will be determined by heat balances between the different parts of the coil. The enthalpy of the air film is assumed to be a simple function of the enthalpy of the air entering the coil and the water temperature. Then, the enthalpy of the air leaving the coil is calcu­lated with an enthalpy balance between the air stream and the air film. To determine whether the enthalpy decrease will lead to a dehumidification or not, we calcu­late the dew point of the entering air stream. If the enthalpy drop leads to a temperature below the dew point we assume that the air leaving the coil is saturated, i.e. RH = 100% (this will not generally be the case in reality). In this case the tempera­ture of the air leaving the coil is calcu­lated from the enthalpy and the information that the air is saturated (we have made a third order poly­no­mial approxi­mation of the relation between the temperature and enthalpy for satu­rated moist air). If, on the other hand, the dew point is not reached, the humidity ratio of the leaving air equals the humidity ratio of the enter­ing air. In this case the temperature of the air leaving the coil is calcu­lated as a function of the enthalpy and the humidity ratio. The relative humidity may then be cal­culated as a function of this temperature and the humidity ratio.

We have chosen to model only the static part of the process from physical relations. The dynamics is modelled as a simple first order relation between the control signal (u) and the water temperature (Twi). The time constant has the nominal value = 30 s.

The water temperature (Twi) is a linear function of the control signal.

u = 0% => Twi = Tair and u = 100% => Twi = Twi0. This corre­sponds to mixing valve control.

Hints

Tai is typically connected to the outdoor temperature or the output of a model that is situated in front of the cooler in the duct. If Tai is con­nected to the outdoor temperature, a disturbance may be introduced by changing this temperature in order to check the response from the tem­perature control loop. Fi is often the relative humidity of the outdoor air. To check the behaviour of the dehumidification control, change the value of the relative humidity of the outdoor air and see how the control system reacts.

Inputs

Tai = temperature of incoming air (°C). Real.

u = control signal (%). Real.

Fi = relative humidity of incoming air (%). Real.

Outputs

TOut = temperature of outgoing air (°C). Real.

FiOut = relative humidity of outgoing air (%). Real.

Constants

qair = air flow through coil (m³/s). Nominal value = 5.0 m³/s. Real.

Patm = atmospheric pressure (Pa) = 101315 Pa. Real.

rho = density of air (kg/m³) = 1.2 kg/m³, at P = 101315 Pa and 20 °C. (1993 ASHRAE HANDBOOK, FUNDAMENTALS). Real.

Uh = "generalised" heat transfer coefficient (kg/s). Nominal value = 20.0 kg/s. A high value on Uh gives a larger heat transfer for a given enthalpy difference between the air film and the air stream. A low value on Uh gives the opposite effect. Real.

c8–c18 = constants in calculation of saturation pressure, see (1993 ASHRAE HANDBOOK, FUNDAMENTALS). Real.

References

ASHRAE. (1992):"1992 ASHRAE HANDBOOK, HVAC Systems and Equipment," SI-edition. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc., Atlanta.

ASHRAE. (1993):"1993 ASHRAE HANDBOOK, FUNDAMENTALS," SI-edition. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc., Atlanta.

2.2.3.  Speed controlled fan (Fan speed)

Description

Fan speed is a model of a fan with speed control. The dynamics from the control signal to the fan speed (rpm) is modelled as a first order system. The rest of the model is static. The model is based on the assumption that one point on the fan curve is known. This point is defined by the air flow (q0), pressure (p0) and fan speed (N0). Other operating conditions is derived from the known operating point and fan laws, cf. 1992 ASHRAE HANDBOOK, pg. 18.4.

The fan speed is assumed to be a linear function of the control signal:

uc=0%    => N=0 and p=0

uc=100% => N=N0 and p=p0

Hints

The Fan speed model may be used for validation of the pressure control in a duct. Note however that the flow output of the Fan speed model does not affect the behaviour of the other models. Therefore the Fan speed model can not be used for checking the how the temperature control is influenced by a varying air flow in the duct.

Inputs

uc = control signal (%). Real.

Outputs

P = fan pressure (Pa). Real.

Qair = air flow (m³/s). Real.

Constants

p0 = fan pressure in known operating point (Pa). Nominal value = 500 Pa. Real.

q0 = air flow in known operating point (m³/s). Nominal value = 5.0 m³/s. Real.

N0 = fan speed in known operating point (rpm). Nominal value = 1400 rpm. Real.

References

ASHRAE. (1992):"1992 ASHRAE HANDBOOK, FUNDAMENTALS," SI-edition. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc., Atlanta.