Оценка уровня пожаробезопасности в жилом секторе Украины по причине разрядов молнии

 

Ковалёв А.П., д.т.н., профессор, Соленая О.Я., аспирант, Ищук В.С., студент

 

Известно, что кучево-дождевые облака создают метеорологические условия для аккумуляции электрических зарядов (гигантский конденсатор).

В момент, когда электростатическое поле достигает критического значения, которое зависит от влажности воздуха и атмосферного давления, происходит природный электрический разряд – молния. Вследствие нагрева воздуха электрической дугой происходит резкое его расширение, которое сопровождается громом.

Во Франции ежегодно происходит около 1 млн/год ударов молнии в наземные объекты. В результате ударов молнии (за год): от 20-40 погибает людей; 20000 животных поражаются молнией; 20000 несчастных случаев; до 15000 пожаров, вызванных ударами молнии; 50000 вышедших из строя электросчетчиков; 250 поврежденных колоколен [1].

По данным МЧС за период 2005 – 2011 гг. в Украине произошло N=117 пожаров по причине удара молнии. В бытовом секторе зафиксирован m=21 случай.

Интервалы времени до первого пожара в часах, начиная наблюдение с 01.01.2005 г. и до 25.07.2011 г., представлены в виде вариационного ряда и занесены в таблицу 1:

 

Таблица 1 – Исходные данные и расчетные параметры

i	ti, ч.	xi	Mi	xi+1- xi		а	с
1	2	3	4	5	6	7	8
1	5670	8,643	1,024594	0,768	0,75	0,01355	-0,034
2	12222	9,411	0,525657	0	0	0,01703	-0,0364
3	12227	9,411	0,360159	0,627	1,741	0,02025	-0,0376
4	22889	10,038	0,278117	0,002	0,007	0,02337	-0,0381
5	22919	10,04	0,229551	0	0	0,02646	-0,0379
6	22921	10,04	0,197821	0,301	1,522	0,02956	-0,0372
7	30982	10,341	0,175815	0	0	0,03271	-0,0359
8	30983	10,341	0,160009	0	0	0,03593	-0,034
9	30984	10,341	0,148471	0	0	0,03925	-0,0316
10	30985	10,341	0,140087	0	0	0,04272	-0,0285
11	30986	10,341	0,134200	0	0	0,04635	-0,0246
12	30987	10,341	0,130451	0,223	1,709	0,05021	-0,0198
13	38705	10,564	0,128702	0,201	1,562	0,05435	-0,0138
14	47353	10,765	0,129025	0,009	0,07	0,05885	-0,0064
15	47777	10,774	0,131756	0	0	0,06384	0,0028
16	47778	10,774	0,137659	0	0	0,06949	0,0149
17	47779	10,774	0,148341	0,081	0,546	0,07612	0,031
18	51804	10,855	0,167481	0,105	0,627	0,08434	0,0542
19	57519	10,96	0,205352	0	0	0,09566	0,092
20	57522	10,96	0,306285			0,11986	0,2214

 

Пусть - первые r порядковых статистик  - время до первого пожара по причине ударов молнии. В нашем случае . Введем обозначение x_i = lnt_i. Тогда статистика, которая лежит в основе критерия Манна, будет иметь вид [2]:

 

                                                                                                                          ,                                                                                                                                                              (1)

где

– обозначает наибольшее целое число, меньшее или равное .

Значения М_i, а также S_kr приведены в таблицах приложения 13 [2].

Гипотеза о том, что данная статистика не противоречит закону распределения Вейбулла правомерна, если:

S < S_kr.

Используя данные таблицы 1 и формулу (1), находим S = 0,52. Критическое значение S_kr находим с помощью приложения 13 [2] для случая, когда  и α = 0,95, тогда S_kr = 0,65. Ввиду того, что S < S_kr, гипотеза является правомерной.

Находим параметры функции распределения Вейбулла.

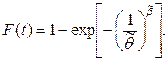                                                                                                                                                              (2)

Оценки первоначальных параметров распределения Вейбулла:

                                                                                                                                                                  (3)

                                                                                                                                                                  (4)

Параметры  и  находятся следующим образом:

                                                                                                                                                         (5)

                                                                                                                                                                  (6)

где

 и  - линейные весовые множители.

Используя данные приложения 9 [2] для случая   находим значения  и  и заносим их в колонки 7 и 8 таблицы 1.

Используя данные колонок 3, 7 и 8 таблицы 1 и формулы (5) и (6), находим:  

Подставляя полученные значения в формулы (3) и (4), находим:  

Оценку математического ожидания и стандарта можно определить по формулам [3].

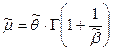.                                                                                                                                                        (7)

                                                                                                                                          (8)

Подставляем полученные значения  и  в формулы (7) и (8) и значения Г(1,77), полученные с помощью таблицы [3], находим:  ч. и  ч.

Подставив полученные оценки параметров распределения в формулу (2), получим:

                                                                                                                                       (9)

Используя вариационный ряд таблицы 1 колонки 2, строим статистическую функцию распределения (рис.1).

С помощью формулы (9) строим функцию распределения интервалов времени до первого возгорания в жилом секторе из-за ударов молнии и наносим ее на статистическое распределение (рис.1).

Рисунок 1 – Статистическая  и аппроксимирующая функции распределения интервалов времени между пожарами в жилом секторе по причине удара молнии

 

Полученная функция распределения (9) позволяет ответить на вопрос, какова вероятность того, что на Украине в течение времени  произойдет возгорание в жилом секторе по причине удара молнии.

Выводы

1. В Украине за 7 лет произошло 117 пожаров по причине ударов молнии, из них 21 сопровождался возгоранием в бытовом секторе.

2. Установлено, что интервалы времени до первого пожара в бытовом секторе по причине ударов молнии не противоречат функции распределения Вейбулла с параметрами  ч. и  ч.

 

Литература

1. Patrick Abati Protection contre la foudre dans les installations BT. [Электронный ресурс] - sitelec.org/cours/abati/foudre/foudre.htm

2. Капур К., Ламберсон Л. Надежность и проектирование систем. Перевод с английского Коваленко Е.Г., под редакцией д-ра техн. наук, проф. Ушакова И.А. – Издательство «Мир», Москва, 1980. – 604 с.

3. Фундаментальные проблемы теории точности. Коллектив авторов / Под ред. В.П. Булатова, И.Г. Фриндлендера. – СПб.: Наука, 2001. – 504 с., 105 ил.