УДК 621.316.06.019.34.001.24

А.П КОВАЛЕВ (д-р техн. наук, проф.), В.В. ХРАМОГИНА

Государственное высшее учебное заведение

«Донецкий национальный технический университет»

kap@elf.dgtu.donetsk.ua

Oценка живучести узлов нагрузки подстанции 110/6-10 кВ

В данной статье предложен один из возможных вариантов оценки живучести узлов нагрузки подстанции 110/6-10 кВ. В статье получена зависимость, которая позволяет определить, в какой степени увеличивается живучесть узлов нагрузки при уменьшении интервала времени между диагностиками системы отключения защитного коммутационного аппарата. Приведен пример расчета.

Подстанция, секция шин, отказы электрооборудования, узел нагрузки, живучесть, защитный коммутационный аппарат, диагностика системы отключения, параметр потока отказа.

Толчком к развитию методов оценки надежности структурно-сложных схем, прогнозирования цепочечных аварий и живучести энергосистем (ЭС) послужила авария, которая случилась 9 ноября 1965 года в США. Эта авария привела к тому, что на территории с населением 30 млн. человек более чем на 10 часов была прекращена жизнедеятельность. Ущерб от аварии составил более 100 млн. долларов [1].

Более 65 % крупных аварий можно отнести к цепочечным, которые происходят в динамическом режиме при коротком замыкании (КЗ) в элементе сети и отказе в срабатывании ряда защитных коммутационных аппаратах, через которые прошел сквозной ток КЗ и привел в действие их релейные защиты [2].

В энергетике под живучестью объекта понимается свойство противостоять возмущениям, не допуская их каскадного развития с массовым нарушением питания потребителей [3].

Под живучестью узла нагрузки будем понимать способность потребителей и их автоматических средств защиты противостоять возмущениям, которые приводят его к аварийному отключению [4].

В работе [5] предложена общая формула, с помощью которой возможно оценить живучесть конкретной ЭС.

                   (1)

где

H_r – частота появления аварий, которая характеризует живучесть ЭС (либо отдельных ее частей);

λ_j – параметр потока КЗ, происшедших в j-том элементе;

ω_i – параметр потока отказов в срабатывании защитного коммутационного аппарата (ЗКА) через который прошел сквозной аварийный ток при КЗ в j-том элементе сети и привел в действие его токовую защиту;

Θ_i – интервал времени между диагностиками системы отключения ЗКА, в том числе и токовую защиту;

m – число ЗКА, через которые прошел сквозной аварийный ток и привел в действия их токовые защиты;

r – номер энергосистемы или узла нагрузки;

n – число j-тых элементов КЗ, в которых приводит в действие i-тые ЗКА, через которые прошел сквозной аварийный ток и привел в действие их токовые защиты.

Чем меньше H_r, тем живучесть ЭС выше.

В том случае, если , формула (1) примет вид:

              (2)

Формулы (1) и (2) справедливы при выполнении следующих условий:

                                  (3)

– интервалы времени между КЗ и интервалы времени между выявленными отказами в системе отключения ЗКА не противоречат экспоненциальным функциям распределения вероятностей с параметрами и соответственно;

– длительность нахождения ЗКА в необнаруженном отказавшем состоянии не противоречит экспоненциальной функции распределения вероятностей;

При выводе формул (1) и (2) были приняты следующие допущения:

– устройства релейной защиты (РЗ) могут выходить из строя только тогда, когда они находятся в режиме ожидания;

– если к моменту возникновения КЗ в сети, на которое должна реагировать РЗ, она находилась в работоспособном состоянии, то маловероятен ее выход из строя в режиме тревоги [6];

– отказы в схеме РЗ или приводе системы отключения ЗКА выявляются и устраняются только в результате абсолютно надежных диагностических проверок, которые происходят с интервалом времени Θ_i.

Под отказом в срабатывании защитного коммутационного аппарата (ЗКА) будем понимать такой, который приводит к отказу в отключении поврежденного элемента сети при КЗ в зоне действия его релейной защиты [7].

Вероятность выхода из строя r-той ЭС или отдельных ее частей:

                   (4)

если , то .

Узлом нагрузки для трансформаторной подстанции (рис. 1) может быть любая из секций шин - I или II.

Рисунок 1 – Принципиальная схема подстанции 110/6-10 кВ

Живучесть узла нагрузки определяется в динамическом режиме, то есть, когда в отходящих от секции шин линиях или их потребителях случайно происходят короткие замыкания (КЗ).

Характеризовать живучесть узла нагрузки будем параметром потока его аварийного отключения при КЗ в зоне действия токовой защиты i-го коммутационного аппарата, присоединённого к соответствующей секции шин.

Например, если линия Л₁ получает электроэнергию от шины I (рис. 1), то шина I потеряет живучесть при совпадении в пространстве и времени двух случайных событий: – произошло КЗ в линии Л₁ и –произошел отказ в срабатывании выключателя под номером i. В этом случае выключатель под номером m+2, который снабжает электроэнергией секцию I, её отключит с помощью токовой защиты и кроме потребителя, который получал электроэнергию от секции I по линии Л₁, отключатся и все потребители, которые получали электроэнергию от этой секции шин через соответствующие выключатели (i=2...m).

Если обозначить через Н₁ живучесть секции шин I, т.е. параметр потока аварийных отключений секции шин, при КЗ в линиях, потребители которых получают электроэнергию от секции шин I, тогда:

,                    (5)

где

,                                                                                        (6)

λ_j – параметр потока КЗ, происшедших в j-той линии, которая присоединяется к шине I через соответствующий i-тый коммутационный аппарат (j=1...n ), (i=1...m );

a_j – число зафиксированных КЗ, которые произошли в j-том отрезке линии за время наблюдения;

Т – время наблюдения за состоянием линий, которые отходят от секции шин I и II и электрооборудованием подстанции.

,                                                                                        (7)

ω_i – параметр потока отказов в срабатывании системы отключения i-того ЗКА (i=1...m );

Θ_i – интервалы времени между диагностиками системы отключения i-того ЗКА;

b_i – число выявленных в результате диагностики повреждений в системе отключения ЗКА, которые могли бы привести к отказу его в срабатывании при КЗ в зоне действия его токовых защит.

Аналогичным образом считается и живучесть Н₂ секции шин II. В этом случае λ_j – будет параметр потока КЗ в линиях, отходящих от соответствующих коммутационных аппаратов, присоединённых к секции II.

Вероятность аварийного отключения секции шин I в течение времени t можно определить следующим образом:

,                                                                     (8)

где H₁ –живучесть секции I подстанции (параметр потока аварийных отключений секции шин I при КЗ в линиях, потребители которых получают электроэнергию от этой секции шин).

По аналогичной формуле (8) определяется вероятность отключения секции II подстанции, если известна H₂.

Пример. Под наблюдением в течение Т=12 лет находилось электрооборудование подстанции 110/6 кВ, которая снабжала электроэнергией одну из шахт Донбасса. От первой системы шин отходили 4 линии и от II также 4. Схема трансформаторной подстанции аналогична схеме (рис. 1).

За это время было зафиксировано следующие короткие замыкания (КЗ), которые произошли в линиях Л₁, Л₂,…, Л₈:

a₁=3; a₂=4; a₃=2; a₄=6; a₅=5; a₆=3; a₇=1;a₈=0.

Системы отключения ЗКА подстанции проверялись (диагностировались) один раз в год, т.е. Θ=1 год. За время наблюдения 12 лет было выявлено следующее число повреждений, которые могли бы привести к отказу его в срабатывании при КЗ в зоне действия его токовой защиты:

b₁=5; b₂=4; b₃=3; b₄=6; b₅=0; b₆=0; b₇=1;b₈=7.

Построить дерево событий и схемы минимальных сечений, которое объясняет потерю живучести секции I и II.

Определить:

1) живучесть секции I и II;

2) как изменится живучесть секции шин I и II, если диагностировать систему отключения ЗКА будем через Θ=0,5 года;

3) какова вероятность того, что в течение 10 лет при Θ=1 год секции I и II потеряют живучесть.

Решение. Используя исходные данные примера формулы (6), (7) находим следующие параметры потоков КЗ в линиях и в системе отключения ЗКА:

а) для отходящих от секции шин линий:

λ₁=0,25 1/год; λ₂=0,33 1/год; λ₃=0,17 1/год; λ₄=0,5 1/год; λ₅=0,42 1/год; λ₆=0,25 1/год; λ₇=0,08 1/год; λ₈=0.

б) для системы отключения ЗКА:

ω₁=0,42 1/год; ω₂=0,33 1/год; ω₃=0,25 1/год; ω₄=0,5 1/год; ω₅=0; ω₆=0; ω₇=0,08 1/год; ω₈=0,58 1/год;

Анализируя зафиксированные в оперативных журналах результаты наблюдений (Т=12 лет) за появлениями КЗ в отходящих от секции I и II линиях, выявленные и устранённые в ЗКА отказы в системе отключения, которые могли бы привести к отказу их в срабатывании, при случайном появлении КЗ в зоне действия их токовых защит – строим «деревья» и схемы минимальных сечений, которые позволяют объяснить потерю живучести узлов нагрузки (секция I и II) подстанции 110/6 кВ [6].

Обозначим через – событие, произошло КЗ в j-той линии; – событие, произошёл отказ в системе отключения i-того ЗКА.

Каждое из событий и характеризуются параметрами потока КЗ – λ_j и параметром потока отказов в системе отключения ЗКА – ω_i.

Дерево событий, которое объясняет потерю живучести секции I и II имеет вид рис. 2 а, в.

Используя рис. 2 а, в строим схемы минимальных сечений рис. 2 б, г.

Пользуясь формулой (1), значениями параметров λ_j и ω_i , полученными с помощью формул (2) и (3) и схемами минимальных сечений рис. 2 б, г находим:

Если же диагностику системы отключения ЗКА проводить через Θ=0,5 года, тогда:

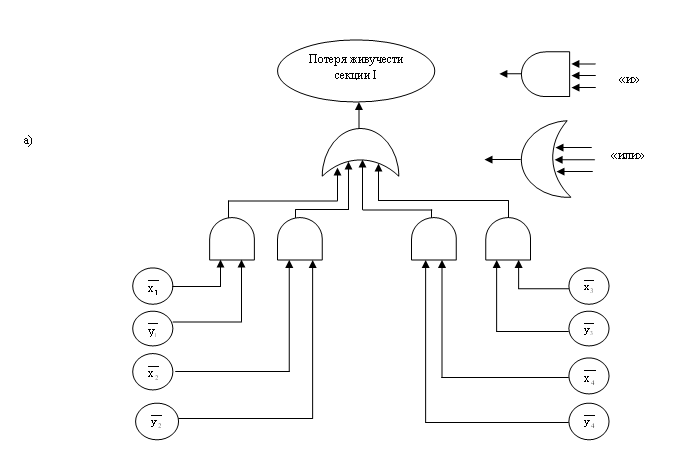
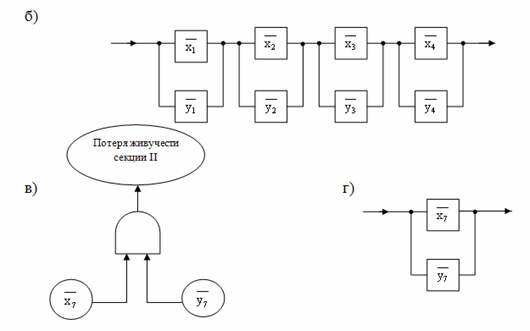
Рисунок 2 – Дерево событий и схемы минимальных сечений
а) произошло событие – КЗ в линии Л_j (j=1...4 ) и – отказал в срабатывании ЗКА (i=1...4 ); б) схема минимальных сечений, составленная для оценки живучести секции I;
в) произошло событие – КЗ в линии Л₇, j=7 и событие – отказал в срабатывании ЗКА, i=7; г) схема минимальных сечений, составленная для оценки живучести секции II.

Определим во сколько раз увеличится живучесть секции шин I и II при уменьшении сроков диагностики системы отключения коммутационного аппарата с Θ=1 год на Θ=0,5 года.

Вероятность того, что в течение t=10 лет при Θ=1 год секции I и II подстанции потеряют живучесть можно оценить с помощью формулы (8):

Выводы

1. Для определения наиболее точной оценки живучести узлов нагрузки подстанции 110/6-10 кВ, наблюдение за электрооборудованием следует проводить не за группами однотипных элементов, а конкретно за каждой его единицей. Чем больше время наблюдения за оборудованием подстанции, тем точнее значение живучести узла нагрузки.

2. Наблюдение за работой электрооборудования подстанции следует начинать с момента ее пуска в эксплуатацию до момента утилизации.

3. Наблюдение в течение T=12 лет за электрооборудованием подстанции 110/6 кВ, которая снабжает электроэнергией угольную шахту, установлено, что живучесть секции шин:H₁=0,108 1/год, а H₂=2,56*10^-3 1/год.

4. Показано, что изменение срока диагностики системы отключения ЗКА 6 кВ с Θ=1 год до Θ=0,5 года позволяет увеличить живучесть секции I и II в 4 раза.

5. Определена вероятность того, что в течение t=10 лет секции I и II подстанции потеряют живучесть: F₁(10)=0,66, а F₂(10)=2,56*10^-3.

Литератyра

1. Prevention of power failures Vol. 3. Studies of the task groups on the northeast power interruption. A report to the federal power commission. June, 1967, 142 p.
2. Гук Ю.Б. Теория надежности в электроэнергетике. – Л.: Энергоатомиздат. Ленинградское отд-ние, 1990. – 208 с.
3. Надежность систем энергетики. Терминология. – М.: Наука, 1980,вып. 95. – 42 с.
4. Ковалев А.П., Якимишина В.В. О живучести объектов энергетики//Промышленная энергетика, №1, 2006. – с. 20-26.
5. Ковалев А.П, Якимишина В.В, Нагорный М.А. Оценка надежности узлов нагрузки подстанции 110/10 кВ//Промышленная энергетика, № 11, 2010. – С. 24-28.
6. Фабрикант В.П. О применении теории надежности к оценке устройств релейной защиты///Электричество, № 9, 1965. – с. 6-9.
7. Эндрени Дж. Моделирование при расчётах надёжности в электроэнергетических системах. Пер. с англ./Под ред. Ю.И. Руденко. – М.: Энергоатомиздат, 1983. – 336 с.
8. Диллон Б., Сингх Ч. Инженерные методы обеспечения надежности систем: Пер. с англ. – М.: Мир, 1984. – 318 с.