«Эстафетный» метод имитации случайных электроэнергетических процессов

Авторы: Куренный Э.Г., Погребняк Н.Н.

Источник: Техническая электродинамика, 1990, №3. – с. 3-6.

Методы статистического моделирования (имитации) применяются для получения реализаций изменения во времени t случайных процессов в сетях электроснабжения промышленных предприятий, а также для решения тех задач, которые не могут быть решены аналитически. Обычно имитируются нормальные случайные процессы, хотя на практике встречаются и другие вероятностные распределения.

Теоретически возможно получить реализации с любыми заданными характеристиками имитацией условных плотностей распределения [2], но такой подход практически невозможно осуществить из-за необходимости решения чрезмерно большого количества уравнений, равного количеству N ординат имитируемой реализации X(t). К тому же получить исходную информацию об условных распределениях довольно трудно. В связи с этим разрабатываются методы имитации, основанные на упорядочении ординат предварительно полученной реализации.

В работе [3] упорядочение осуществляется по экстремумам первой разности и (или) произведения ординат, получаемых от генератора случайных чисел (ГСЧ). Метод не обеспечивает воспроизведения значений корреляционной функции (КФ) К(τ) в контролируемых точках.

В данной статье предлагается «эстафетный» метод (название условное) имитации реализаций стационарных случайных процессов с заданным аналитически или таблично законом вероятностного распределения и КФ любого вида, основанный на упорядочении ординат предварительно смоделированной реализации, не обязательно от ГСЧ. Этот метод может применяться и для улучшения по КФ качества имитации случайных процессов, полученных другими методами [1, 4]. Это связано с тем, что в силу случайного характера реализаций даже теоретически корректные методы имитации могут давать реализации, характеристики которых не соответствуют заданным. В таких случаях обычно реализации исключаются из рассмотрения, а упорядочение ординат позволяет избежать повторных реализаций.

Пусть каким-либо методом получена случайная последовательность ординат процесса 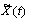, функция распределения которой удовлетворяет заданным требованиям. Среднее значение является устойчивой характеристикой, поэтому можно считать, что оно практически при близости функций распределения не отличается от среднего значения Xс искомого процесса X(t). Очевидно, любая перестановка ординат в пределах длительности Т реализации не изменяет вида распределения и среднего значения, но приводит к изменению КФ.

Ординаты имитируемых процессов разделены малым интервалом Δ при общем их количестве 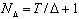. В связи с этим КФ вычисляется по формуле:

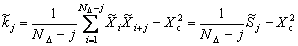               1)

i=τ/Δ — количество интервалов Δ в интервалах t и τ, - сумма произведений ординат моделируемого процесса.

Для искомой КФ согласно (1) требуемые значения сумм составляют:

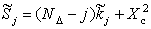
Тогда отличия КФ от заданной в контролируемых точках определяются разностями

                                    2)

Вследствие этого в общем виде необходимо переставить ординаты таким образом, чтобы в любой точке τ=j&Delta: разности (2) были бы минимальны. Практически достаточно выполнения этого условия для характерных точек КФ. Поскольку при хорошем воспроизведении функции распределения дисперсия близка к заданной, то улучшения качества имитации при τ=0 обычно не требуется.

Количество возможных комбинаций перестановок ординат даже при конечном их числе очень велико. Поэтому найти теоретически оптимальный алгоритм минимизации выражений (2) вряд ли возможно. Приемлемое для практики решение удается получить, если осуществлять перестановки по мере появления вариантов, приближающих к заданному решению.

Независимо от количества контролируемых ординат КФ перебор ординат осуществляется по единому алгоритму. Вначале поочередно проверяется возможность перестановки каждой ординаты X(i) с начальной ординатой Х(1). Если в некоторой точке i = r (рис. 1, а) хотя бы по одной контролируемой ординате КФ разность (2) уменьшается, а по остальным по меньшей мере не увеличивается, то ордината Х(r) меняется местами с начальной (рис. 1, б).

После перестановки продолжается пошаговый перебор, но уже оцениваются перестановки ординат при i≥r+1 с ординатой Х(r), занявшей место начальной ординаты. Иными словами, ордината Х(r) как бы передала эстафету ординате Х(1) — отсюда и название метода.

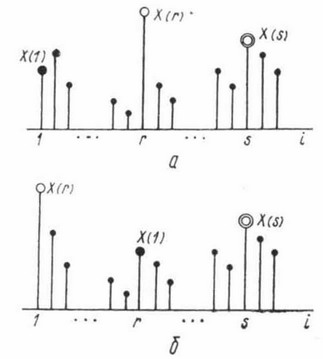
Если в процессе дальнейших переборов встретится новая подходящая ордината X(s), то меняются ординаты Х(r) и X(s), а ордината Х(1) остается на месте i=r. После окончания перестановок относительно i=l вся процедура вновь повторяется, но начиная со второй ординаты.

Численные эксперименты выявили одну особенность: при заданном наибольшем значении τmах контролируемой абсциссы КФ перебор следует начинать не с соседней ординаты, а с отстоящей от начальной на расстоянии jmах=τmах/Δ. Например, при i=1 перебираются ординаты с шагом 1, но начиная с i=1 + jmax, а не с 2. Здесь имеется аналогия с перестановками, которые осуществляются в методе квантования времени [2, 4]: по перемене знака ординат относительно среднего значения можно перемещать любые группы ординат, не приближаясь к соседним на расстояние, меньшее jmax - 1. В противном случае нарушаются ранее согласованные перестановки для j < jmax. По-видимому, такое ограничение по началу перебора является характерным для методов имитации, использующих перестановки ординат или групп ординат.

Эстафетный метод применяется к исходной реализации с любой КФ, лишь бы она имела бы заданное вероятностное распределение.

Предельными являются два случая: исходная реализация принимается в виде упорядоченной диаграммы с детерминированными связями между ординатами или имитируется в виде реального белого шума [1] – случайной последовательности некоррелированных чисел. Проверка показала, что в обоих случаях метод обеспечивает требуемое качество моделирования, однако при упорядоченной диаграмме получается значительно большее количество перестановок, поэтому этот подход не рекомендуется для практики.

Генераторы случайных чисел дают равномерное или нормальное распределения. Для получения распределений другого вида равномерное распределение преобразуется известным преобразованием [2] или по схеме урны с невозвращаемыми шарами [4].

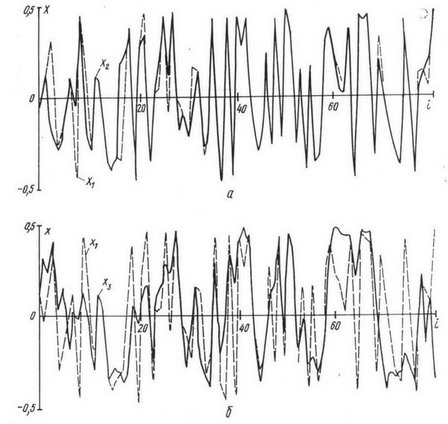
Метод позволяет по одной реализации получить реализации с различными требуемыми КФ. Например, представленная на рис. 2 часть исходной реализации X1(t) была получена на ПЭВМ Искра 1030 от стандартного ГСЧ. Ее КФ показана на рис. 3 ломаной 1. По этой реализации были получены три реализации: X2(t) — реального белого шума с КФ в виде прямоугольного треугольника единичной высоты и основанием Δ (ломаная 4), X3(t) — случайного процесса с экспоненциальной КФ с параметром α = 0,93 1/с; при Δ = 0,4 с, а также процесса с экспоненциально-косинусоидальной КФ (на рис. 2 и 3 не приведены). Отклонения фактически полученных КФ (кривые 2 и 3) от теоретических в контролируемых точках j = 1 ... 5, показанных на рис.3 кружками, не превысили 1 %.

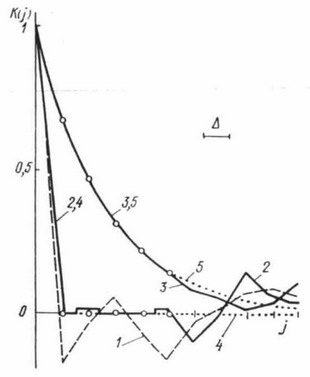
Численные эксперименты выявили устойчивость КФ в области значений аргумента от Δ до времени корреляции или точки τ0 первого пересечения нуля. Это позволяет осуществлять контроль не во всех точках области. Например, для процесса с экспоненциально-косинусоидальной КФ при контроле только в точках Δ и τ0 в промежутках между ними наибольшая погрешность в воспроизведении КФ составила 3,2 %. Следует обратить внимание на обязательность контроля при τ=Δ, поскольку многие характеристики случайного процесса определяются поведением КФ в окрестностях нуля (экстремумы, выбросы и провалы).

Поскольку методы упорядочения не имеют алгоритмов поиска оптимальных решений, то оптимизация осуществляется в процессе численного эксперимента. В методе работы [3] приходится подбирать константы упорядочения и длину предыстории. В рассматриваемом методе после завершения перестановок ординат на месте первой ординаты обязательно оказывается другая ордината, что позволяет повторять упорядочение до тех пор, пока не будет получено наилучшее решение. Такая оптимизация может оказаться целесообразной при использовании имитационных методов для численного доказательства не имеющих аналитического обоснования предположений.

Таким образом, применение эстафетного метода позволяет имитировать реализации электроэнергетических процессов с заданными вероятностными распределениями и корреляционными функциями любого вида.

1. Куренный Э. Г., Дмитриева Е. Н., Петрушечкина Л. М., Пушная И. В. Имитация графиков электрической нагрузки преобразованием белого шума // Техн. электродинамика – 1986. – № 6 – С. 56 – 62.
2. Соболь И. М. Численные методы Монте-Карло. – М.: Наука, 1973. – 311 с.
3. Хамитов Г. П. Упорядочение в моделировании случайных функций// Автоматизированные системы управления, теория, методология, технические средства. – Иркутск, 1972 – С. 22 – 38.
4. Шидловский А. К., Куренный Э. Г. Введение в статистическую динамику систем электроснабжения. – Киев: Наук, думка, 1984. – 273 с.